Complementary Angles – Explanation & Examples
What is a Complementary Angle?
Complementary angles are pair angles with the sum of 90 degrees. When talking about complementary angles, always remember that the angles appear in pairs. One angle is the complement of the other angle.
Although a right angle is 90 degrees, it can’t be called a complementary because it doesn’t appear in pairs. It is just a complete one angle. Three angles or more angles whose sum is equal to 90 degrees cannot also be called complementary angles.
Complementary angles always have positive measures. It is composed of two acute angles measuring less than 90 degrees.
Common examples of complementary angles are:
- Two angles measuring 45 degrees each.
- Angles measuring 30 and 60 degrees.
- Angles measuring 1 degree and 89 degrees.
A complimentary angle can be adjacent angles.
For example,
∠ STA= 65 degrees and ∠ATR= 25 degrees are adjacent complementary angles.
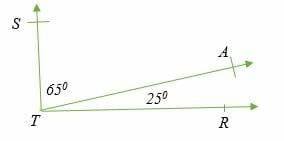
We can also have complementary angles that are not adjacent to each other.
For example,
∠ DGO= 20 degrees and ∠ ODG= 70 degrees are pairs of complementary angles that are not adjacent to each other.
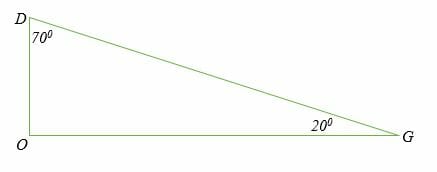
Another important property to note about complementary angles is that two complementary angles don’t have to be in the same figure.
So long as the angles add to 90 degrees, they are complementary.
For example:
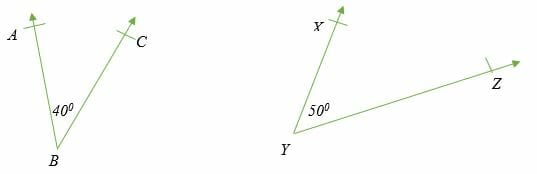
The two angles in the above different figures are complementary.
∠ABC + ∠ XYZ = 90 degrees
How to Find a Complementary Angle?
Since we know that complementary angles add to 90 degrees, we can easily calculate the value of any angle by subtracting the given angles from 90 degrees.
Example 1
Calculate the complement angle of 33°.
Solution
Subtract the given angle from 90°.
90° – 33°
= 57°
Therefore, the complement of 33° is 57°
Example 2
Determine the missing angle in the following figure
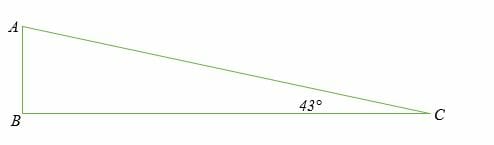
Solution
∠ABC + ∠ACB + 90° = 180°
Therefore, ∠BAC + ∠ACB = 90° (complementary angles)
∠BAC + 43° = 90°
∠BAC = 90°- 43°
∠BAC = 47°
Example 3
Find the complement of 27°20′
Solution
90° – 27°20′
= 89°60′ – 27°20′
= 62°40′
Therefore, the complement of 27°20′ is 62°40′
Example 4
Find the angle that is 46° less than its complement.
Solution
Let x be the unknown angle.
(90 – x) – x = 46°
90 – x – x = 46°
90 – 2x = 46°
90 – 90 – 2x = 46° – 90
-2x = 46° – 90
-2x = 46° – 90
-2x = -44°
2x = 44°
x = 44/2
x = 22°
Therefore, 90 – 22 = 68°
Example 5
If the difference between two complementary is 18 degrees, find the angles.
Solution
Let the smaller angle be x degrees, and the bigger angle will be (90 – x) °.
(90° – x) – x = 18°
90° – 2x = 18°
x = 72°/2
x = 36°
90° – x
= 90° – 36°
= 54°.
Therefore, the two complementary angles are 36° and 54°.
Example 6
Calculate the value of x in the following figure:
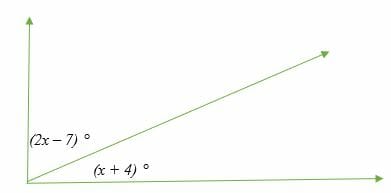
Solution
⟹ (2x – 7) ° + (x + 4) ° = 90°
⟹2x + x – 7° + 4° = 90°
⟹ 3x – 3° = 90°
⟹ 3x – 3° + 3° = 90° + 3°
⟹ 3x = 93°
⟹ x = 93°/3
⟹ x = 31°
Example 7
Find the complement angle of 2/3 of 90 degrees.
Solution
⟹ 90° x 2/3 = 60°
⟹ 90° – 60° = 30°
Therefore, the complement angle is 30°
Example 8
Determine the complement angle of (x + 10) °.
Solution
⟹ (x + 10) ° = 90° – (x + 10) °
= 90° – 10° – y°
= (80 – x) °
Example 9
Two complementary angles are such that one of the angles is twice the sum of the other angle plus 3 degrees. Find two complementary angles.
Solution
Let the two angles be x and y degrees.
⟹ x + y = 90°
One of the angles is twice the sum of the other angle plus 3 degrees.
⟹ x = 2(y + 3)
⟹ x = 2y + 6
We now solve the two simultaneous equations by substitution.
⟹ 2y + 6 + y = 90
⟹ 3y + 6 = 90
⟹ 3y = 84
⟹ y = 28
⟹ x = 2(28) + 6
⟹ x = 56 + 6
⟹ x = 62
