360 Degree Angle – Explanation and Examples

A 360 degree angle, or a full angle, is the interior angle measure of a circle.

In radians, a full angle measures $2\pi$ radians.

$360$ degree angles play an important role in mathematics, including geometry and trigonometry, and science, including astronomy and physics. They’re also important in engineering, architecture, and design.

Before moving on with this section, review angles and types of angles.

This section covers:

• What is a 360 Degree Angle?
• 360 Degree Angle vs. Zero Angle
• 360 Degree Angle Definition
• Full Angle Examples

What is a 360 Degree Angle?

A $360$ degree angle is a full turn or a “full angle.” It is also the interior angle measure of a circle and the sum of the interior angles of a quadrilateral.

In radians, a full angle measures $2\pi$ radians.

Turning an object $360$ degrees gets it back to its starting position and original orientation.

360 Degree Angle vs. Zero Angle

A 360 degree angle and a zero angle might look the same. This is because if an object rotates zero degrees or $360$ degrees, the end result is the same.

The process, however, is different. In once case, nothing has moved. In the other case, the object has made a full circle.

Because of this fact, however, trigonometric functions are $2\pi$ cyclic. That is, their values repeat for every $2\pi$ or $360$ degrees. That is, the properties of a $360$ degree angle will be the same as that of a $0$ degree angle.

360 Degree Angle Definition

A $360$ degree angle is a full turn. It is equal to $2\pi$ radians or the interior angle of a circle.

Full Angle Examples

The most classic example of a full angle is the unit circle.

This is a circle with a radius of one centered at the origin. Such a circle has a circumference of $2\pi$, and the arc length of any section of the circumference has the same length as the radian measure.

These circles are used in trigonometry because it is easy to draw right triangles in this circle that have simple measurements, making trigonometric ratios easy to find.

The total angle measure of the unit circle is $360$ degrees. When dealing with angles greater than $360$, ratios are found by subtracting $360$ degrees or $2\pi$ radians as many times as needed until the result is a number, $k$, greater than or equal to $0$ and less than $360$. Then, the ratio for the initial angle is equal to the ratio at $k$.

Examples

This section goes over common examples of problems involving full angles and their step-by-step solutions.

Example 1

Prove that a quadrilateral has an internal angle sum equal to $360$ degrees.

Solution

There are a few ways to do this. One way involves knowing that a triangle has an internal angle sum equal to $180$ degrees or the measure of a straight line.

This fact has been known since antiquity and can be proved without measuring the angles. In fact, Euclid has a proof of this fact in his Elements in proposition 32.

But, connecting two triangles produces a quadrilateral.

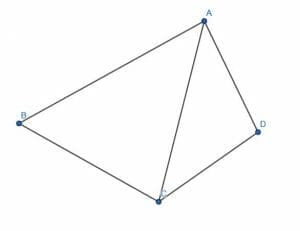
Therefore, the sum of the internal angles of the quadrilateral must be equal to the sum of the internal angles of two triangles. That is, the internal angles sum must be equal to the measure of two straight lines.

But, two straight lines is a full angle. Therefore, the internal angle measure of a quadrilateral is $360$ degrees or $2\pi$ radians.

Example 2

Find an angle greater than or equal to $0$ degrees and less $360$ that is equivalent to $567$ degrees. Classify this angle.

Solution

A full angle and a zero degree angle lie on the same line and point the same direction. At this point, the angles reset. Therefore, a $360$ degree angle acts the same as a $0$ angle. Similarly, a $361$ degree angle has the same properties as a $1$ degree angle.

Therefore, to find an angle with the same properties, subtract $360$ degrees or $3\pi$ from an angle repeatedly until the difference is a number between $0$ and $360$.

In this case, $567-360 = 207$. Therefore, the angle with a measure of $567$ degrees will have the same properties as a $207$ degree reflex angle.

Example 3

An analogue clock reads 4 o’clock. After the minute hand makes a $360$ degree turn, what time will it be? How many degrees will the hour hand have turned in the same time?

Solution

When the minute hand makes a $360$ degree turn, it gets back to where it started. Since the initial time was 4 o’clock, the minute hand started on the twelve. After the turn, it will be back on the twelve.

When the minute hand makes a complete circuit around the clock, one hour has passed. Therefore, the hour hand will move from being directly on the four to directly on the five. This means that the hour hand will have moved $\frac{1}{12}$th of a circle. In degrees, that is $\frac{360}{12} = 30$ degrees. In radians, it is $\frac{2\pi}{12} = \frac{\pi}{6}$ radians.

Example 4

A circle has a radius of $4$. Find the length of a segment of circumference with an arclength of $360$ degrees.

Solution

The arclength of a segment is the length of a circle’s circumference that is contained by a given angle formed by the center of the circle and two radii.

An arclength of $360$ degrees means the angle formed by the two radii is a full angle. But, this is also the total interior angle of a circle. Therefore, the length of the segment of the circumference contained by this angle is the full circumference.

The circumference of this circle is $8\times\pi = 8\pi$.

Example 5

Show that the sum of an interior angle and its corresponding exterior angle in a polygon make a full angle.

Solution

The interior angle of an angle in a polygon is the smaller of two possible angles. The other angle, which will be a reflex angle, is the same angle measured in the opposite direction (clockwise or counterclockwise).

These two angles, when put together create a circle. Therefore, their angle measure is $360$ degrees or $2\pi$ radians, the same as a full angle.

More Examples and Explanation

1. Prove that if a quadrilateral is added to a triangle such that two of the lines of the quadrilateral lie in line with two of the lines of sides of the triangle and another side of the quadrilateral is equal to the third side, then the new figure is a triangle. 
2. An hour hand on a clock makes a $360$ degree turn. What is the new time and how many degrees has the minute hand turned?

Answer Key

1. A triangle and a quadrilateral with one shared side will create a figure with $3+4-2 = 5$ sides and angles. Its total interior angle measure will be $540$ degrees.
   This pentagon, however, has two straight angles because two of the sides of the quadrilateral lie in line with two sides of the triangle. Each straight angle in a polygon effectively makes it have one less side. In this case, the total number of sides will be $5-2 = 3$. Therefore, the resulting figure will be a triangle.
2. If an hour hand makes a $360$ degree turn, then twelve hours have passed. This means that the time is the same, but AM or PM has changed. For example, if the starting time was 8 AM, the new time is 8 PM.
   Since the minute hand makes a $360$ degree turn once per hour, it has made a $360 \times 12 = 4320$ degree turn.

Illustrations/mathematical objects created with GeoGebra.