- Home
- >
- Complementary Events
JUMP TO TOPIC
Complementary Events – Explanation & Examples
 Can you think of events that cannot happen at the same time? On a given day, you can either go to school or not. It can either rain, or not. When you toss a coin, you can get a head or not. When you pick a card from a deck it can be red, or it can be black. These are all examples of complementary events.
Can you think of events that cannot happen at the same time? On a given day, you can either go to school or not. It can either rain, or not. When you toss a coin, you can get a head or not. When you pick a card from a deck it can be red, or it can be black. These are all examples of complementary events.
Thus, we have the definition:
Events in which one outcome can only happen if another does not are called complementary events.
In this lesson we will explore:
- Complementary Events
- How to find the probability of complementary events
Let’s get to it!
What are complementary events?
 Let’s revisit the events mentioned above. The event that you do not go to school is the complement of the event that you go to school, and vice versa. The complement of getting a head is getting a tail. The complement of getting a red card, is getting a black card. Therefore, you can think of complements as the “nots”. The event that we do not want. Stated in another way:
Let’s revisit the events mentioned above. The event that you do not go to school is the complement of the event that you go to school, and vice versa. The complement of getting a head is getting a tail. The complement of getting a red card, is getting a black card. Therefore, you can think of complements as the “nots”. The event that we do not want. Stated in another way:
The complement of an event is the outcome, or outcomes in which it does not occur.
Intuitively, this means that the sum of the probabilities of complementary events is 1. Mathematically, we express this as:
$P(B) + P(B’) = 1$
$⇒P(B) = 1 – P(B’)$
$⇒P(B’) = 1 – P(B)$
Where:
B – the event
B’ – the complement of the event (called B prime) The complement is sometimes written with a superscript c instead of an apostrophe.
These three equations are equivalent and are different ways of writing the same relationship. This relationship is referred to as the complement rule.
Complementary events are mutually exclusive events since they cannot occur at the same time. They are also considered as exhaustive events since the sum of their probabilities must be 1.
How do you find the probability of complementary events?
We can determine the probabilities of complementary events using the complement rule.
$P(B) + P(B’) = 1$
Where:
B – the event
B’ – the complement of the even
Say the probability that you go to school on a given day is $\frac{7}{8}$, then the probability that you do not go is $1 – \frac{7}{8} = \frac{1}{8}$. We can express this as follows.
Let B represent the event that you go to school, then:
$P(\text{B}) = \frac{7}{8}$
$P(\text{B’}) = 1 – \frac{7}{8} = \frac{1}{8}$
Usefulness of the Complement Rule
It is useful to know this rule when the sample space of the desired event consists of a large number of outcomes. As a basic example, let S be the event of getting two unique digits when you toss two dice. To find P(S) it is more convenient to find the probability of S’, the event that the result has doubles, then subtract it from 1.
$\text{S’ = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}}$
$P(\text{S’}) = \frac{6}{6×6} = \frac{6}{36} = frac{1}{6}$
Thus: $P(\text{S}) = 1 – \frac{1}{6} = \frac{5}{6}$
Instead of listing all the outcomes in the sample space of S and of the experiment, we only had to determine
- the number of outcomes in S’
- the number of outcomes in the sample space of the experiment
Note
In some cases it will be useful to list the outcomes of the event or its complement in order to compute the desired probability. We will examine this in examples 1 and 2. Example 3 looks at another event that only has two possible outcomes.
Example 1: Let A represent the event that you get a 2 when you toss a die. What is P(A’)?
Solution:
This can be solved in two ways.
Method 1: Determine P(A) then find P(A’) using P(A’) = 1 – P(A)
A = {2}
$P(\text{A}) = \frac{1}{6}$
Therefore $P(\text{A’}) = 1 – \frac{1}{6} = \frac{5}{6}$
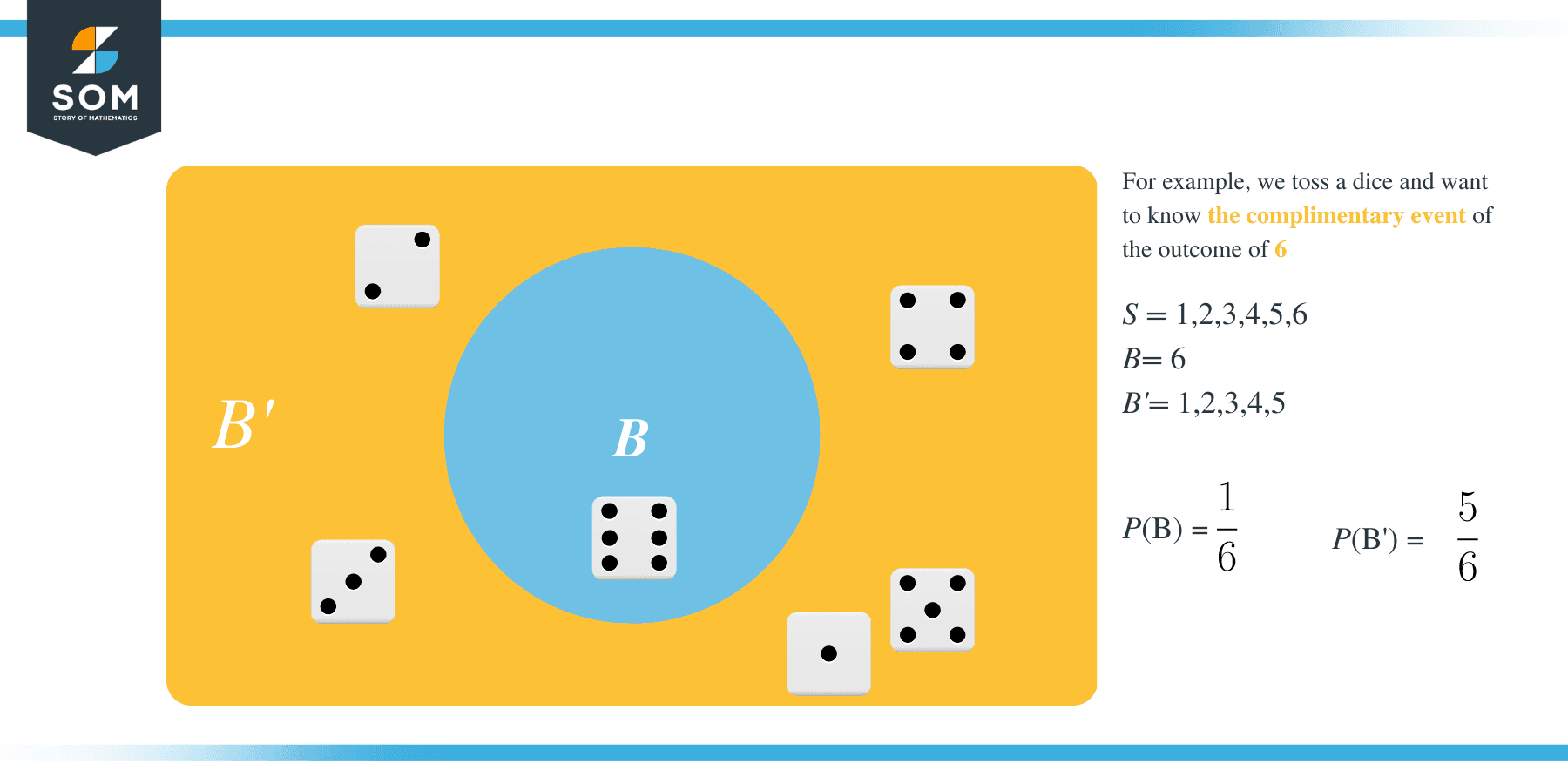 Method 2: Determine the outcomes in A’, then find P(A’).
Method 2: Determine the outcomes in A’, then find P(A’).
A’ is made up every outcome that is not 2.
Thus $A’ = {1, 3, 4, 5, 6}$
Since these are 5 of the 6 outcomes we get:
$P(\text{A’}) = \frac{5}{6}$
Example 2: A delivery trailer is hauling 10 cars. 3 of the cars are black, 2 are white, 1 is red, 2 are blue, and 2 are silver. Let C be the event that a car chosen at random is a primary color. What is P(C’)?
Using Method 1
$\text{C = {1 red, 2 blue}}$
$P(\text{C}) = \frac{1+2}{10} = \frac{3}{10}$
Therefore $P(\text{C’}) = 1 – \frac{3}{10} = \frac{7}{10}$
Using Method 2:
C’ is the event that a car chosen at random is not a primary color therefore we have:
$\text{C’ = {3 black, 2 white, 2 silver}}$
$P(\text{C’}) = \frac{3+2+2}{10} = \frac{7}{10}$
Example 3: A lemonade stand has pink and plain lemonade. If the probability of buying pink lemonade is 3/8, what is the probability that the customer does not buy pink lemonade? Of 40 customers, how many do you expect to buy plain lemonade?
Let L represent the event that a customer buys pink lemonade. Then:
$P(\text{L}) = \frac{3}{8}$
$P(\text{L’}) = 1 – \frac{3}{8} = \frac{5}{8}$
Since the only other option is plain lemonade, P(L’) is equal to the probability that the customer buys plain lemonade.
Therefore, of 40 customers we expect:
$\frac{5}{8} × 40 = 25$ to buy plain lemonade.
Try these examples!
Practice Questions
- If A is the event that a bus misses its schedule and $P(\text{A}) = \frac{1}{15}$, what is P(A’)?
- If B’ is the event that you do not get a head when you toss a coin, what is P(B)?
- If C is the event that you pick a red card from a 52-card deck, what is P(C’)?
- A bag contains 5 blue, 3 yellow, and 6 green marbles. If D is the event that you pick a green marble, what is P(D’)?
- A 5-seater vehicle is carrying 3 adults and 2 children. If E is the event that a person chosen at random is an adult, what is P(E’)?
Solutions
Question 1
$P(\text{A’}) = 1 – \frac{1}{15} = \frac{14}{15}$
Question 2
B’ – the event that you do not get a head is equivalent to the event of getting a tail.
$P(\text{B}) = 1 – P(\text{B’}) = 1 – \frac{1}{2} = \frac{1}{2}$
Question 3
Since the deck only has red or black cards:
$P(\text{C’}) = 1 – \frac{26}{52} = \frac{26}{52} = \frac{1}{2}$
Question 4
Method 1:
D = {6 green}
$P(\text{D}) = \frac{6}{14} = \frac{3}{7}$
Therefore: $P(\text{D’}) = 1 – \frac{3}{7} = \frac{4}{7}$
Method 2:
D’ = {5 blue, 3 yellow}
$P(\text{D’}) = \frac{5 + 3}{14} = \frac{8}{14} = \frac{4}{7}$
Question 5
Method 1:
E = {3 adults}
$P(\text{E}) = \frac{3}{5}$
Therefore: $P(\text{E’}) = 1 – \frac{3}{5} = \frac{2}{5}$
Method 2
E’ = {2 children}
$P(\text{E’}) = \frac{2}{5}$
