Probability

Probability is the study of events and how likely they are to happen. This likelihood is usually expressed as a fraction. The denominator expresses the total number of possible events in a given situation while the numerator expresses the number of ways that the indicated event can happen. Sometimes this fraction is converted to a decimal or a percentage, depending on the situation.

The two most common situations that most people think of when they hear probability are the weather and games of chance.

In the days leading up to an outdoor event, many people anxiously check the weather report seeing what the “chance” of rain is. Most know that a 10% chance of rain means it is unlikely while a 90% chance of rain means rain is likely.

These probabilities, while grounded in the science of meteorology, are not usually calculated by examining all possible situations, as that is impossible. Instead, they are educated guesses based on past experiences and meteorological conditions.

Most games of chance, however, can be represented mathematically by probabilities.

For example, the probability of a coin flip landing on heads is ½, and the probability of a coin flip landing on tails is ½. The probability of a die landing on the number three is 1/6, but the probability of the die landing on an even number is 3/6=1/2.

The key with games of chance is that they also usually include a monetary value and psychological component. This is why some probabilities about games of chance, such as the famous Monty Hall problem, surprise people. Their intuition of the probability is different from the probability calculated mathematically. This is also why “the house always wins” in any casino.

Probability is closely related to the mathematical subject of combinatorics, which is also discussed in this guide. Whereas probability determines the likelihood of events based on the number of possible events and favorable outcomes, combinatorics seeks to determine the number of possible events and favorable outcomes. While that may seem simple for something like rolling a die or flipping a coin, it gets much more complicated when considering the possible number of five card hands drawn from a 52-card deck.

Both probability and combinatorics provide an important base for further mathematical study in statistics and graph theory. Because statistics is useful in every kind of social and physical science and graph theory provides a lot of the basis of computer and network studies, probability is used in just about every subject in some way or another.

This resource guide begins by explaining what is meant by the concept of an “event” in theoretical and concrete circumstances. It then gives strategies for finding the likelihood of events, including the construction of tree diagrams and conditional probability.

The guide then introduces combinatorics for the calculation of probabilities before ending with an exploration of how probability is used in both basic and advanced statistics.

Diagrams and Conditional Probability

Just as probability is used to determine the likelihood of individual events, it can be used to determine the likelihood of compound events. Consider, for example that someone, instead of tossing a coin once, tossed it twice.

The first toss would either yield heads or tails. The second coin toss would also yield heads or tails. The possible outcomes for such an experiment are heads-heads, heads-tails, tails-heads, and tails-tails.

This can of course quickly become complicated for experiments that have more than two outcomes or that are performed more than twice. That is what makes tree diagrams, a kind of probabilistic flow chart, so useful. They provide a way of organizing the likelihood of different events in an experiment.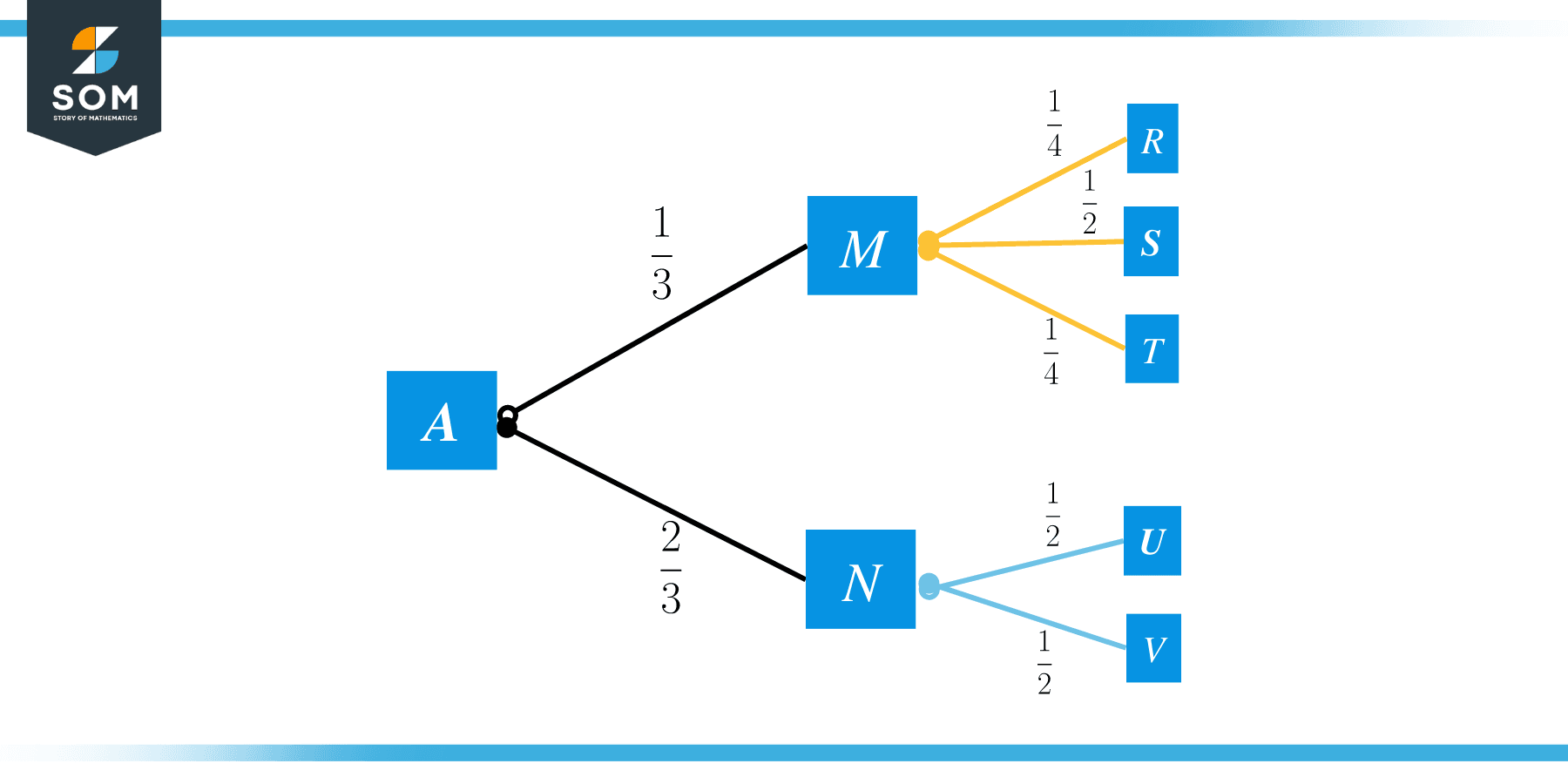

This topic begins by explaining tree diagrams and other ways of visually constructing probabilities. It then introduces concepts used to calculate compound events, namely mutual exclusivity, independence, and dependence. These concepts are used to determine conditional probability, or the probability of one thing given another.

Finally, the subject ends by exploring the difference between probability with and without replacement.

Events

Probability relies on the likelihood of events, but what is an event?

An event can be thought of as an outcome. In a coin flip, there are two possible outcomes: heads and tails.

When rolling a die, there are 6 possible outcomes: 1, 2, 3, 4, 5, 6.

When selecting a card from a deck, there are 52 possible outcomes.

All of these outcomes are equally likely, but events do not have to be equally likely. For example, the possible outcomes of a blood type test are O, A, B, and AB. In the United States, the probability that a person chosen at random will have O is 0.44 or 44%, not 0.25 or 25%.

This topic introduces samples and the probability of events by comparing theoretical and experimental probability. It also explains event complements.

The section ends by providing examples of uses of these probabilities, including geometric applications and coin and dice problems.

Combinatorics

Many people have heard that a Rubik’s cube has 43,252,003,274,489,856,000 different possible configurations.

That number is read as “forty-three quintillion, two-hundred fifty-two quadrillion, three trillion, two-hundred seventy-four billion, four-hundred eight-nine billion, eight-hundred fifty-six thousand.” Even reading the number aloud at a normal speed takes almost twenty seconds!

How did people determine this incredibly large number?

Rather than try each one and write it down to make sure there were no repeats (a process that would take about 1.4 trillion years if it took one second to try and record each configuration), mathematicians used combinatorics.

Combinatorics is the mathematics of counting large numbers of possibilities. It uses factorials, permutations, and combinations to do that. Permutations are the number of ways to rearrange a group of objects where the order matters. Combinations are groupings of objects from a set where the order does not matter. Factorials are used to help calculate both of these.

This topic begins by explaining how to use factorials and their application is permutations and combinations. It ends by relating these concepts to statistics.

Probability Used in Statistics

Perhaps the most famous use of probability in other branches of mathematics is its use is statistics. Statistics typically takes a sample of a population and extrapolates using probability to make determinations about the population itself. This section explores those applications by looking at the mathematics behind them.

The topic begins by explaining what a random variable is and why randomness matters in probability and statistics. It also explains how to use probability to determine a probability density function. The section also discusses different distribution functions used in statistics and how they are used to determine an expected value. Finally, the section concludes with how to calculate and use z-scores and Bayes’ theorem.