- Home
- >
- Factorial – Explanation & Examples
JUMP TO TOPIC
Factorial – Explanation & Examples
In probability theory, there are many scenarios in which we have to calculate all the possible arrangements of a given set.
For example, if we toss a coin $10$ times, what would be the size of sample space?
Or if we want to select a team of $5$ people from $10$ available members, how many different teams can we make? Factorial is a mathematical operation that helps us in figuring out such arrangements and hence plays an important role in probability theory.
A factorial (denoted by ‘ ! ‘) is defined as the product of all positive integers that are less than or equal to a given positive integer.
After reading this article, you should understand:
- Factorial
- How to calculate factorials
- How factorials are used to evaluate permutations
- How factorials are used to evaluate combinations
- How factorials are used to find probabilities
It would be advisable to refresh the following topics:
1. Fundamental counting principle
2. Permutations
3. Combinations
What Is a Factorial
The factorial of a positive integer $n$ is defined as the product of all positive integers that are less than or equal to $n$. The factorial is denoted by that integer and an exclamation mark, i.e., “!“.
Example 1:
What is the factorial of $ 6?$
Solution:
The numbers less than or equal to $6$ are $6,\,5,\,,4,\,3\,,2\,,1$. Therefore,
$6! = \large {6 \times 5 \times 4 \times 3 \times 2 \times 1 } $ = $ 720 $.
Example 2: Evaluate $ \large {\frac{7!}{4!} } $.
Solution:
$\frac{7!}{4!}$ = $\large {\frac{7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{4 \times 3 \times 2 \times 1}} $
= $\large{ (7 \times 6 \times 5)} $
= $210$
Factorial Formula:
For any integer $n$, we can define a formula for factorial as follows:
$n! = n \times (n-1) \times (n-2) \times \cdots \times 2 \times 1$.
We can also use the product notation, i.e., $ \prod$ to succinctly write the formula as follows
$n! = \prod_{k=0}^{n-1} (n-k)$
Factorial Rules
Let us tabulate the factorials of the first few numbers in the table below:
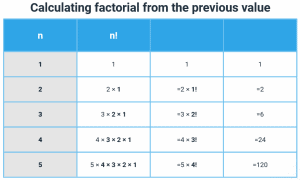
It becomes obvious from the above table that the factorial of any integer $ n $ can be calculated from the factorial of the previous integer, i.e., $ n-1 $. We can state the factorial rule as follows:
$ n! = n \times (n-1)! $
The factorial rule simplifies the calculations of complex expressions involving factorials. An interesting application of the factorial rule is in the evaluation of $ 0! $. If we want $ 1 $ to follow the factorial rule, then:
$ 1! = 1 \times 0! $.
However, from the formula of the factorials, it is obvious that $1! = 1$. Hence,
$1 = 1 \times 0!$.
This means that $0!=1$. Note that factorial is not defined for negative integers, and hence factorial rule cannot be applied on $0$.
How to Do Factorials
When doing factorials, it is advisable to apply the factorial rule whenever possible to simplify expressions, as shown in the examples below
Example 3: Evaluate $\large{\frac{6!}{3 \times 4!}}$.
Solution:
Using the factorial rule, we can write
$6! = 6 \times 5!$
However, we have $4!$ in the denominator, so we apply factorial rule again on $5!$ to get
$6! = 6 \times 5 \times 4!$. Accordingly,
$\large{\frac{6!}{3 \times 4!} = \frac{6 \times 5 \times 4!}{3 \times 4!} = \frac{6 \times 5}{3} = 10}$.
Example 4: Evaluate $\large{\frac{11!}{5!\times 8!}}$.
Solution:
= $\large {\frac{11 \times 10 \times 9 \times 8!}{5!\times 8!} }=\large{ \frac{11 \times 10 \times 9}{5.4.3.2.1}}= \large{\frac{990}{120}}= 8.25 $.
Applications of Factorials:
In probability theory, factorials are extensively used in the evaluation of permutations and combinations. We discuss both these applications below:
Factorials and Permutations:
The possible arrangements of a given set of objects are called permutations. For instance, let’s suppose we have a set of three numbers $\{1,2,3\}$. There are six possible permutations (i.e., arrangements) of the these three numbers, i.e., $\{1,2,3\}, \, \{1,3,2\}, \, \{3,1,2\}, \, \{3,2,1\}, \{2,3,1\}$ and $\{2,1,3\}$. Generally, in problems involving permutations, we are given a set of $n$ objects, and we are asked to find all possible arrangements if $k$ objects are chosen out of the total $n$ objects and are referred to as “$n$ choose $k$” permutations. For instance, we might be given $10$ numbers from $0$ t0 $9$, and we could be asked to find all possible ways in which we can select three numbers out of the given $10$ numbers. There are two different types of permutations that can be performed on any given set.
1. Permutations in which we can repeat the objects from the available set.
2. Permutations in which repetitions are not allowed.
We will focus on the second type of permutations only as these are the ones that involve factorials.
Permutations Without Repetition:
Let us suppose we have $n$ objects, and we have to find all possible arrangements when $k$ out of $n$ objects are chosen without repetition. As shown in the figure below, there are $n$ possible ways to select the first item.
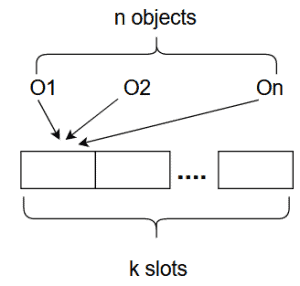
Once the first item has been selected, there are $n-1$ objects left as we are not allowed repetitions. Hence there are $n-1$ ways to select the second item, as shown in the figure below.
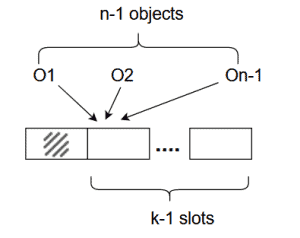
Similarly, there are $n-2, n-3$ possibilities for the third and fourth selection, and finally, we will have $n-(k-1)$ possible selections for the last $k$th item.
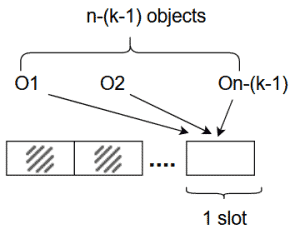
Using the fundamental counting principle, the total permutations are
$\textrm{Total permutations for n choose k} = P(n,k) = n \times n-1 \times n-2 \times \cdots \times n-(k-1)$.
We multiply and divide the above expression with $(n-k)!$ to get
$P(n,k) = \frac{n \times n-1 \times n-2 \times \cdots \times n-(k-1) \times (n-k)!}{(n-k)!}$.
From the factorial rule discussed above, we note that
$n \times n-1 \times n-2 \times \cdots \times n-(k-1) \times (n-k)! = n!$
Hence, the formula for $n$ choose $k$ permutations, without repetition is given as
$P(n,k) = \frac{n!}{(n-k)!}$.
Example 5: How many 4 letters words can be formed out of the letters of the word “Employ” when repetition is not allowed?
Solution:
The word “employ” has six letters so $n=6$ and we have to form all possible four-letter words without repetition hence $r=4$. Therefore, possible permutations can be calculated as:
$ P(n,r) = \large{\frac{n!}{(n-r)!}}$
$P(6,4)=\large{\frac{6!}{(6-4)!}}$
$P(6,4)=\large{\frac{6\times 5\times 4\times 3\times 2 \times 1}{(2\times 1)}}$
$P(6,4)=360$
Example 6: How many $5$-digits numbers can be formed by using the digits $1,2,3,4,5,6,7$ only once?
Solution:
We have seven digit in total and we choose 5 digits for the permutations, hence
$P(7,5)=\large{\frac{7!}{(7-5)!}}$
$P(7,5)=\large{\frac{7\times 6\times 5\times 4\times 3\times 2\times1}{(2\times1)}}$
$P(5,3)=2520$
Permutations with non-distinct objects:
In some situations, we have a set of non-distinct objects, and we are interested in finding the possible permutations. For instance, in how many different ways can we arrange the letters in the word MISSISSIPPI? In total we have 11 letters, so $n=11$. Since we are interested in the arrangements of all the letters so $r=11$ in this case. For simplicity, we limit our discussion to such cases only where $n=r$.
If all letters had been distinct, we would have gotten $P(n,r) = \frac{n!}{(n-r)!} = n!$ permutations. However, “S” appears four times, “I” appears four times, and “P” appears twice. So, there would be $4!$ permutations of “S” that would result in the same arrangement of the $11$ letters of MISSISSIPPI. Similarly, there would be $4!$ arrangements of “I” and $2!$ arrangements of “P” that would result in the same permutation. Therefore, we can write
$\textrm{Permutations if letters had been distinct} =\textrm{Permutations of non distinct letters} \times 4! \times 4! \times 2! $
Rearranging the above equation
$\textrm{Total permutations of non distinct letters} =\large{ \frac{n!}{4! 4! 2!}}$.
$\textrm{Total permutations of non distinct letters} = \large{\frac{11!}{4! \times 4! \times 2!} }$= $34650$.
Generally, if we have a set of $n$ objects and there are $n1$ items that are the same, and $n2$ items that are the same but different from $n1$ and $n3$ similar items that are different from $n1$ and $n2$ etc., then the formula for permutations can be written as
$\textrm{permutations of non distinct items} = \large{\frac{n!}{n1! \times n2! \times n3!}}$
Example 7:
In how many different ways can we arrange the letters in the word $\text{TOOTH}$?
Solution:
There are $5$ letters in $\text{TOOTH}$ so $n=5$. “T” appears twice so $n1=2$ and “O” appears twice to $n2=2$. Hence
$\textrm{Permutations of the Word TOOTH} = \frac{n!}{(n1! \times n2!)}$
$\textrm{Permutations of the Word TOOTH} = \frac{5!}{(2! \times 2!)} = \frac{5\times4\times3}{2} = 30$.
Example 8:
How many $6$ letter words can be formed using the letters in the word $\text{BANANA}$?
Solution:
In this case, $n=6$, $n1=3$ (i.e., three “A”s) and $n2=2$ (i.e., two “Ns”). The total permutations are
$\textrm{Permutations of the word BANANA} = \frac{6!}{ 3! \times 2!}$
$\textrm{Permutations of the word BANANA} = \frac{6 \times 5 \times 4 \times 3!}{3! \times 2!}$
$\textrm{Permutations of the word BANANA} = \frac{6 \times 5 \times 4}{2!} = 60$
Factorials and Combinations:
The evaluation of possible combinations is another interesting application of the factorial. Similar to permutations, combinations are possible arrangements of a set of given items. The difference between permutations and combinations is that, in combinations, the order of the arrangements does not matter, whereas, in permutations, the order of the arrangement matters.
For instance, let us suppose we are interested in possible arrangements of the numbers $1,2,3, 4$ using three numbers only. If we treat $1,2,4$ as one possible arrangement and $4,2,1$ as another arrangement, then we are dealing with permutations. However, if we treat $1,2,4$ and $4,2,1$ and $2,1,4$, etc., as the same arrangement, i.e., we disregard the order and only focus on the elements, then we are dealing with combinations.
There are many scenarios when order naturally does not matter when arranging a set of objects. For example, let’s say we have a group of four people. Let’s call those Jack, Jill, Liz, and Henry. We wish to make the team consisting of three people using the available group. How many distinct teams can we make? Note that in this scenario, it does not make sense to treat $\{Jack Jill Liz\}$ as one team and $\{Jill Jack Liz\}$ as another team. Obviously, no matter how we order three people, it would results in the same team. Such situations are handled by the concept of combinations and not by permutations.
Combinations Formula:
Let us suppose we have a set of $n$ distinct objects, and we are interested in choosing $k$ objects out of those $n$ objects. How many possible arrangements of $k$ objects can we make if the order does not matter?
Similar to the case of permutations, there are $n$ ways to fill the first slot out of the available $k$ slots. Then there are $n-1$ ways to fill the second slot and so on. Finally, we will have $n-k$ ways to fill the $k$th slot. Now we have a collection of $k$ objects, and these $k$ objects can be rearranged in $k!$ different ways among themselves. Since we are disregarding order in this scenario so the $k!$ re-arrangements would result in the same combination. Hence, we can write
$n \times n-1 \times \cdots (n-k) = \textrm{Total number of distinct Combinations} \times k!$.
Therefore,
$\textrm{Total number of distinct Combinations} = \frac{n \times n-1 \times \cdots (n-k)}{k!}$.
Now multiplying and dividing the right-hand-side of the equation by $(n-k)!$, we get
$\textrm{Total number of distinct Combinations} = \frac{n \times n-1 \times \cdots (n-k) \times (n-k)!}{k!(n-k)!}$.
Using the factorial rule, we can write
$\textrm{Total number of distinct Combinations} = \frac{n!}{k!(n-k)!}$.
We will use the notation $C(n,r)$ to denote the possible combinations of $n$ distinct objects when we choose $k$ objects out of the $n$ available objects.
Example 8: We have a group of four people. Let’s call those Jack, Jill, Liz, and Henry. We wish to make the team consisting of three people using the available group. How many distinct teams can we make?
Solution:
We have already discussed that in this scenario, order of the arrangements does not matter and hence we are dealing with possible combinations with $n=4$ and $k=3$. Using the formula for combinations, we get
$C(4,3) = \frac{4!}{3!(4-3)!} = \frac{4!}{3!1!} = \frac{4 \times 3!}{3!} = 4$.
Example 9: A soccer team consisting of $ 11 $players is to be formed from a pool of $ 15$ players. In how many ways can a team be selected if the Captain is to be included in every team?
Solution:
Since we have to include the captain in every team, so essentially, we have a pool of 14 players and 10 places in the team. When we are selecting a team of individuals, it does not matter in which order the members were selected, and we get the same team if we have the same members. Therefore, we are dealing with combinations in this question, and the possible ways in which a team can be selected are $C(14,10)$
$(C14,10) = \frac{14!}{10!(14-10)!} = \frac{14 \times 13 \times 12 \times 11 \times 10!}{10!4!}$
$C(14,10) = \frac{14 \times 13 \times 12 \times 11}{4!} = 1001$
Factorials and Probabilities
Factorials help us evaluate permutations and combinations. Let us see some examples of how permutations and combinations (and hence factorials) appear in probability questions.
Example 10:
Suppose we randomly pick four alphabets without repetition to form a word. What is the probability that the word does not contain a vowel?
Solution:
Since we are randomly picking up alphabets, so all four-letter words (whether meaningful or not) are equally likely. Let us first calculate how many possible words we can make, i.e., the total number of elements in the sample space of our experiment. Since there are $26$ alphabets in the English language and we are choosing $4$ of them without repetition; hence the total number of possible worlds would be $P(26,4)$.
$\textrm{Total number of possible words} = P(26,4) = \frac{26!}{(26-4)!} = \frac{26 \times 25 \times 24 \times 23 \times 22!}{22!} = 358800$.
Now we want to find the total number of words without vowels. There are $5$ vowels in the alphabets. If we discard the vowels, we are left with $21$ alphabets to make the four-letter words. There will be $P(21,4)$ words that do not contain the vowels, i.e.,
$\textrm{Total number of words without vowels} = P(21,4) = \frac{21!}{(21-4)!} = \frac{21 \times 20 \times 19 \times 18 \times 17!}{17!} = 143640$.
Hence the probability of randomly choosing a four letter word that does not contain a vowel is
$P(\textrm{Choosing a random word without vowels}) = \frac{143640}{358800} = 0.4 = 40\%$
Example 10:
We have a class of nine students, five boys and four girls. We randomly choose to make a team of 4 people. What is the probability that the team will contain only one boy?
Solution:
Let us first find the total number of possible teams, i.e., the number of elements in our sample space. Since we are dealing with a team of people, so the order in which the members are chosen does not matter, and we would get the same team. Hence, the total number of possible teams would be $C(9,4)$, i.e.,
$C(9,4) = \frac{9!}{4!(9-4)!} = \frac{9 \times 8 \times 7 \times 6 \times 5!}{4!5!} = \frac{3024}{24} = 126$.
Now there are $ 5%%EDITORCONTENT%%nbsp; different ways to choose one boy for a team. Once a boy is chosen, we are left with three slots and four girls. Hence, there are be $C(4,3)$ possible ways to choose the remaining team,
$C(4,3) = \frac{4!}{3!(4-3)!} = 4$.
Using the fundamental counting principle(link), there are $5 \times 4$ ways to choose a team with one boy only. Accordingly,
$P(\textrm{Choosing a team with only one boy}) = \frac{12}{126} = 0.095 = 9.5\%$
Practice Questions:
Find the following factorials
1.
a) $4!$
b) $8!$
c) $\frac{8!}{4!}$
d) $\frac{7!}{4!2!(7-2)!}$
2. How many different signals can be given by 4 LEDs of different colors while using 3 LEDs at the same time?
3. An internet account is locked with a four-digit password. The password only contains numbers from 0-6.
a) How many different password options will you have if the order of numbers does that matter.
b) How many different password options will you have if the order of numbers matters.
4. Suppose we randomly pick four alphabets without repetition to form a word. What is the probability that the word does not contain “IT” in it?
5. We have a class of $10$ students, $6$ boys, and $4$ girls. We randomly choose to make a team of 4 people. What is the probability that the team will contain at least one boy?
6. Show that $C(19,18) + C(19,17) = C(20,18)$
Answer Key
1.
a) 24
b) 40320
c) 1680
d) 0.875
2. 24
3.
a) 35
b) 840
4. 0.36%
5. 99.5%
