- Home
- >
- Theoretical Probability – Explanation & Examples
JUMP TO TOPIC
Theoretical Probability – Explanation & Examples
 Imagine a game of selecting one bottle from ten unique bottles. Theoretically, you have a $\frac{1}{10}$ chance of selecting any bottle. However in reality, that may not be the case because $\frac{1}{10}$ chance is theoretical. Theoretical probability is defined as:
Imagine a game of selecting one bottle from ten unique bottles. Theoretically, you have a $\frac{1}{10}$ chance of selecting any bottle. However in reality, that may not be the case because $\frac{1}{10}$ chance is theoretical. Theoretical probability is defined as:
The probability that we expect based on the number of favorable outcomes and the total possible outcomes.
In this lesson we will answer the following questions:
- What is theoretical probability?
- How do we find theoretical probability?
Let’s begin!
What is a theoretical probability?
Let’s revisit the scenario above. There are ten bottles and we will name them B1 – B10. Theoretically, if you were to select a bottle at random, you should get B1 on 1 out of 10 chances. However in reality, you may never get B1. In that case it would mean you selected some bottles more than once. What we expected is possibly different from what we get. This expectation is thought of as the theoretical probability of the event.
Theoretical probability is defined as the expected outcome of an experiment.
This expectation depends on what we know. We know that there are 10 bottles. Therefore, we have 10 possible outcomes. We know that there is one B1 in the set. Thus, the number of outcomes favorable to the event of choosing B1 is 1. This means the theoretical probability of choosing B1 is $\frac{1}{10}$.
This theoretical probability can be extended to larger numbers of trials. For example, if you now had 100 trials, we would expect that on 10 of those trials you will get B1. This is because we expect 1 in every set of 10 trials.
Numerically:
$P(\text{B1 on 1 trial}) = \frac{1}{10}$
Thus from 100 trials we expect to get B1:
$\frac{1}{10} × 100 = 10 \text{ times}$
This can be written as:
$P(\text{B1 on 100 trials}) = \frac{10}{100}$

How do we find theoretical probability?
Now that we understand the meaning of theoretical probability, let’s see how to find it. Theoretical probability is found by:
- Identifying or calculating the number of outcomes favorable to the particular event
- Identifying or calculating the total number of possible outcomes
- Dividing (1) by (2)
Mathematically:
$\text{Theoretical Probability} = \frac{\text{number of outcomes favorable to the event}}{\text{total number of possible outcomes}}$
Carefully read through the following examples.
Example 1: Tommy has a bag of candies. There are 5 of candy A, 3 of candy B, and 1 of candy C. What is the probability of selecting candy A? Candy B? Candy C?
Solution:
Candy A
- Number of candy A = 5
- Total number of candies = 9
- $P(\text{candy A}) = \frac{5}{9}$
Candy B
- Number of candy B = 3
- Total number of candies = 9
- $P(\text{candy B}) = \frac{3}{9} = \frac{1}{3}$
Candy C
- Number of candy C = 1
- Total number of candies = 9
- $P(\text{candy C}) = \frac{1}{9}$
Example 2: What is the probability of getting a prime number when picking a card from a 52-card deck of cards?
Solution:
- Number of cards with prime numbers = 16
- Total number of cards in the deck = 52
- $P(\text{prime number}) = \frac{16}{52} = \frac{4}{13}$
Here are a few examples that require some more calculations.
Example 3: What is the probability of throwing doubles when you toss 2 dice?
Solution:
- Possible number of doubles = 6
- Total number of possible outcomes = 6 × 6 = 36
- $P(\text{doubles}) = \frac{6}{36} = \frac{1}{6}$
You can verify that there are 36 total possible outcomes in our article on sample space. There we showed you how to use a chart to find the sample space of an experiment.
Example 4: In a given semester, a student can take 3 classes. For the first class the student can choose either Biology, Chemistry, or Physics. For the second English or Mathematics. For the third, History, Art, or Music.
a. What is the probability that the student chooses Biology, Mathematics, and Music?
b. What is the probability the student will be taking Mathematics?
c. What is the probability the student will be taking Music?
Solution:
Before we do the calculations, here is a tree diagram. It shows the possible paths and makes it easier to approach the question.
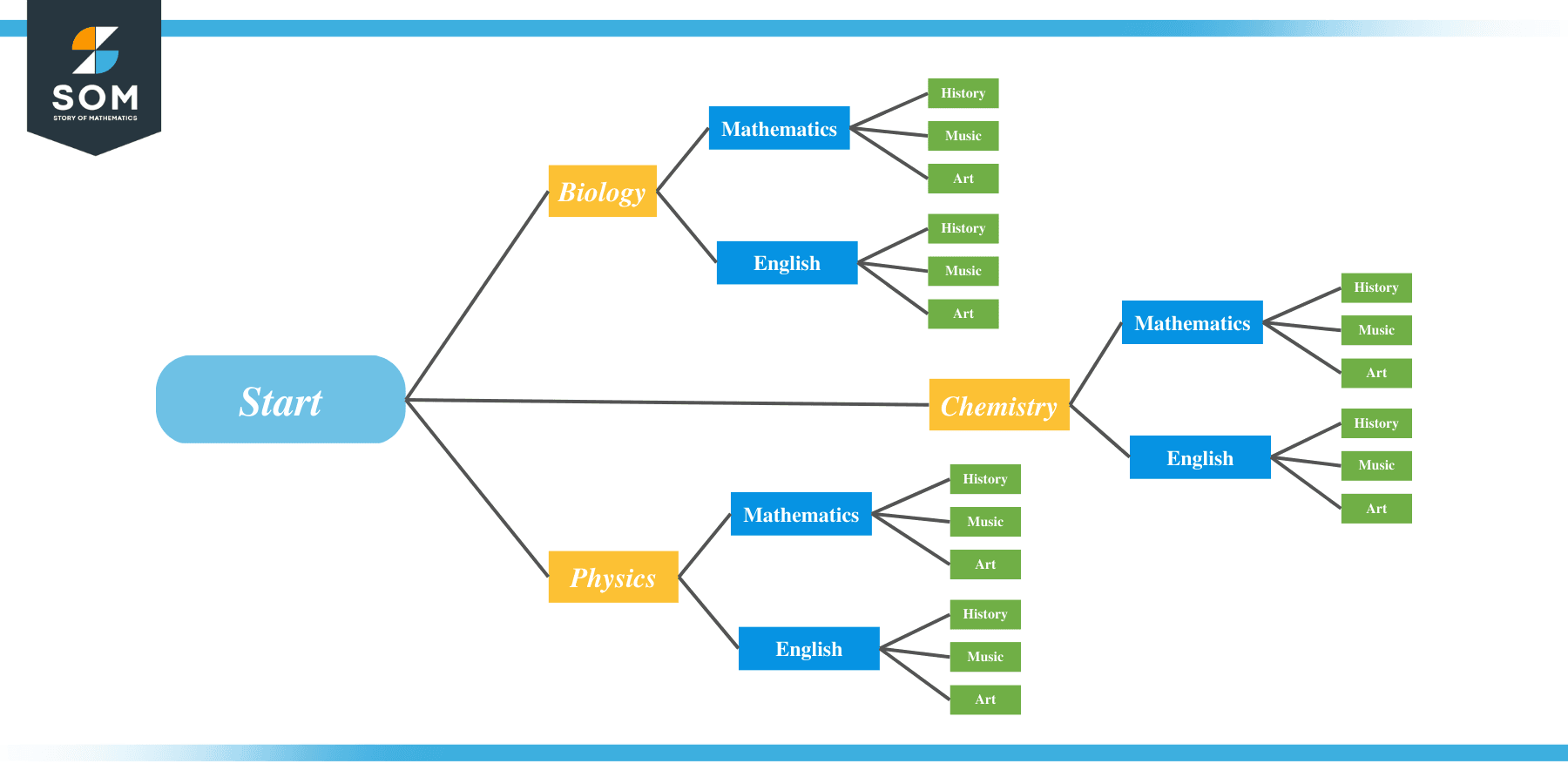
Part A – Solution:
- Number of outcomes with Biology, Mathematics, and Music = 1
- Total number of possible outcomes = 3 × 2 × 3 = 18
- $P(\text{Biology, Mathematics, Music}) = \frac{1}{18}$
Part B – Solution:
- Number of outcomes with Mathematics = 3 × 1 × 3 = 9
- Total number of possible outcomes = 3 × 2 × 3 = 18
- $P(\text{Mathematics}) = \frac{9}{18} = \frac{1}{2}$
Notice that the student still has the same number of choices for the first and third classes. As a result, the expectation here is the same as the expectation of just choosing Mathematics from Mathematics and English. Let’s verify this with the next question.
Part C – Solution:
- Number of outcomes with Music = 3 × 2 × 1 = 6
- Total number of possible outcomes = 3 × 2 × 3 = 18
- $P(\text{Music}) = \frac{6}{18} = \frac{1}{3}$
As expected, $\frac{1}{3}$ is the same as if we had just done the probability of Music from History, Music, or Art.
Now it’s your turn to try some questions.
Practice Questions
Complete the following questions by determining the theoretical probabilities.
- What is the probability of getting an even number when an 8-sided die with faces numbered 1 to 8 is thrown?
- At the supermarket Maria can choose from 3 types of bread, type 1, type 2, and type 3. Each type are fully stacked with 40 loaves. If chosen at random, what is the probability of choosing a type 2 bread?
- On a lot, there are 100 cars for sale. They are evenly distributed across 5 unique colors. If a car is chosen at random, what is the probability of choosing a specific color?
- If you toss a coin 10 times, how many times do you expect to get a Head?
- Martin is playing a game of chance. He gets to roll a die 12 times. If he wins the game by throwing a 6, how many times should he expect to win?
Solutions
Question 1:
What is the probability of getting an even number when an 8-sided die with faces numbered 1 to 8 is thrown?
$P(\text{Even number}) = \frac{4}{8} = \frac{1}{2}$
Question 2:
At the supermarket Maria can choose from 3 types of bread, type 1, type 2, and type 3. Each type are fully stacked with 40 loaves. If a type is chosen at random, what is the probability of choosing a type 2 bread?
$P(\text{type 2}) = \frac{40}{(3*40)} = \frac{40}{120}$
$P(\text{type 2}) = \frac{1}{3}$
Question 3:
On a lot, there are 100 cars for sale. They are evenly distributed across 5 unique colors. If a car is chosen at random, what is the probability of choosing a specific color?
$P(\text{a specific color}) = \frac{20}{100} = \frac{1}{5}$
Question 4:
If you toss a coin 10 times, how many times do you expect to get a head?
$P(\text{Head}) = \frac{1}{2}$
Therefore we expect to get heads: $\frac{1}{2} × 10 = 5 \text{ times}$
Question 5:
Martin is playing a game of chance. He gets to roll a 6-sided die 12 times. If he wins the game by throwing a 6, how many times should he expect to win?
$P(\text{throwing 6}) = \frac{1}{6}$
Therefore he should expect to win: $\frac{1}{6}× 12 = 2 \text{ times}$.
