Compound Inequalities – Explanation & Examples
Compound inequalities are the derived form of inequalities, which are very useful in mathematics whenever dealing with a range of possible values.
For example, after solving a particular linear inequality, you get two solutions, x > 3 and x < 12. You can read it as “3 is less than x, which is less than 12. Now, you can rewrite it in the form of 3 < x < 12. You can read this as x lies between 3 and 12. Therefore, compound inequalities is a professional way of writing the linear inequalities (where possible).
Let’s look at now what a compound inequality is.
What is Compound Inequality?
There are other cases where you can use inequality to represent more than one constraining value. In such situations, a compound inequality is applied.
Therefore, we can define a compound inequality as an expression containing two inequality statements either joined by the words “AND” or by “OR.”
The “And” conjunction indicates that two statements are true at the same time.
On the other hand, the word “Or” implies that the entire compound statement is true as long as one of the statements is true.
The “Or” term is used to denote a combination of the solution sets for the individual statements.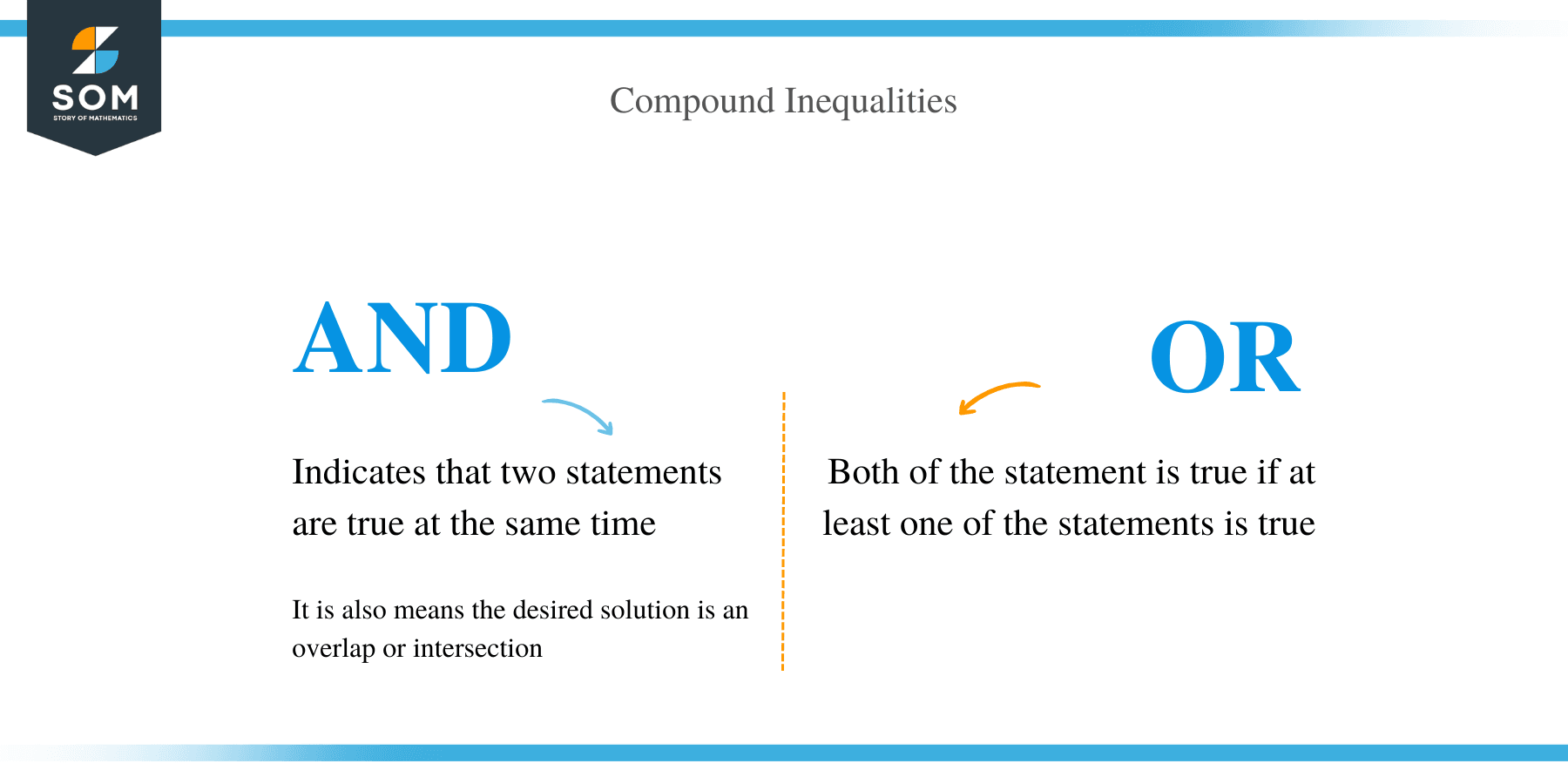
How to Solve Compound Inequalities?
The solution for compound inequalities depends on whether the words “and” or “or” are used to connect the individual statements.Example 1
Solve for x: 3 x + 2 < 14 and 2 x – 5 > –11.
Solution
To solve this compound inequality, we will start by solving each equation separately. And since the joining word is “and,” then it means the desired solution is an overlap or intersection.
3x + 2 < 14
Subtract 2 and divide by 3 on both sides of the equation.
3x + 2 – 2 < 14 -2
3x/3 < 12/3
x < 4 And; 2x – 5 > -11
Add 5 to both sides and divide all by 2
2x – 5 + 5 > -11 + 5
2x > -6
x > -3
The inequality x < 4 indicates all numbers to the left of 4, and x > –3 indicates all the numbers to the right of –3. Therefore, the intersection of these two inequalities includes all numbers between –3 and 4. The solution for these compound inequalities is hence, x > –3 and x < 4
Example 2
Solve 2 + x < 5 and -1 < 2 + x
Solution
Solve each inequality separately.
2 + x < 5
To isolate the variable from the first equation, we need to subtract both sides by 2, which gives;
x < 3.
We again subtract 2 from both sides of the second equation -1 < 2 + x.
-3 < x.
Therefore, the solution for this compound inequality is x < 3 and -3 < x, or -3 < x < 3.
Example 3
Solve 7 > 2x + 5 or 7 < 5x – 3.
Solution
Solve each inequality separately:
For 7 > 2x + 5, we subtract both sides by 5to get;
2 > 2x.
Now divide both sides by 2 to get;
1 > x.
For 7 < 5x – 3, add both sides by 3 to get;
10 < 5x.
Dividing each side by 5 gives;
2 < x.
The solution is x < 1 or x > 2
Example 4
Solve 3(2x+5) ≤18 and 2(x−7) <− 6
Solution
Solve each inequality separately
3(2x + 5) ≤ 18 => 6x + 15 ≤ 18
6x ≤ 3
x ≤ ½
And
2(x−7) <− 6 => 2x −14<−6
2x < 8
x < 4
The solution is therefore, x ≤ ½ and x < 4
Example 5
Solve: 5 + x > 7 or x – 3 < 5
Solution
Solve each inequality separately and combine the solutions.
For 5 + x > 7;
Subtract both sides by 5 to get;
x > 2
Solve x – 3 < 5;
Add 3 to both sides of the inequality to get;
x < 2 Combining the two solutions with the word “or” gives; X > 2 or x < 2
Example 6
Solve for x: –12 ≤ 2 x + 6 ≤ 8.
Solution
When a compound is written without the connecting word, it is assumed to be “and.” Therefore, we can translate x – 12 ≤ 2 x + 6 ≤ 8 into the following compound sentence:
–12 ≤ 2 x + 6 and 2 x + 6 ≤ 8.
Now, we can solve each inequality separately.
For –12 ≤ 2 x + 6;
=> –18 ≤ 2 x
–9 ≤ x
And for 2 x + 6 ≤ 8;
=> 2 x≤ 2
The inequality –9 ≤ x means that all numbers to the right of and including –9 and are within the solution, and x ≤ 1 means that all the numbers to the left of and including 1 are within the solution. The solution this compound inequality can therefore be written as {x| x ≥ –9 and x ≤ 1} or {x| –9 ≤ x ≤ 1}
Example 7
Solve for x: 3x – 2 > –8 or 2 x + 1 < 9.
Solution
For 3x – 2 > –8;
=> 3x – 2 + 2 > –8 + 2
=> 3x > – 6
=> x > – 2
For 2 x + 1 < 9; Subtract 1 from both sides of the equation; => 2 x < 8. => x < 4. The inequality x > –2 implies that the solution is true to all the numbers to the right of –2, and x < 4 implies that, the solution is true to all the numbers to the left of 4. The solution is written as;
{x| x < 4 or x > – 2}
