Congruent Triangles – Explanation & Examples

You must be well aware of the photocopy machine. When you put an A4 page inside the machine and activate it, you get an identical copy of that page. If you rotate or flip the page, it will remain the same as the original page. Even if you cut them out, you can line them up again easily. We can say the pages are similar or congruent.

Further, the A4 page is in a rectangular shape, so when you cut it diagonally, you will get the triangle. If you cut both the photocopies in the same manner, you will see both of them form the same kind of a triangle, which has the same sets of angles and sides.

What is a Congruent Triangle?

You must be well aware of a triangle by now — that it is a 2-dimensional figure with three sides, three angles, and three vertices. Two or more triangles are said to be congruent if their corresponding sides or angles are the same. In other words, Congruent triangles have the same shape and dimensions.

Congruency is a term used to describe two objects with the same shape and size. The symbol for congruency is ≅. In triangles, we use the abbreviation CPCT to show that the Corresponding Parts of Congruent Triangles are the same.

Congruency is neither calculated nor measured but is determined by visual inspection. Triangles can become congruent in three different motions, namely, rotation, reflection, and translation.

What is Triangle Congruence?

Triangle congruences are the rules or the methods used to prove if two triangles are congruent. Two triangles are said to be congruent if and only if we can make one of them superpose on the other to cover it exactly.

These four criteria used to test triangle congruence include:

Side – Side – Side (SSS), Side – Angle – Side (SAS), Angle – Side – Angle (ASA), and Angle – Angle – Side (AAS).

There are more ways to prove the congruency of triangles, but in this lesson, we will restrict ourselves to these postulates only.

Before going into the detail of these postulates of congruency, it is important to know how to mark different sides and angles with a certain sign which shows their congruency. You will often see the sides and angles of a triangle are marked with little tic marks to specify the sets of congruent angles or congruent sides.

You will see in the diagrams below that the sides with one tic mark are of the same measurement, the sides with two tic marks also have the same length, and the sides with the tic marks are equal. The same goes for the angles.

Side – Angle – Side

Side Angle Side (SAS) is a rule used to prove whether a given set of triangles are congruent. In this case, two triangles are congruent if two sides and one included angle in a given triangle are equal to the corresponding two sides and one included angle in another triangle.

Remember that the included angle must be formed by the two sides for the triangles to be congruent.

Illustration of SAS rule:

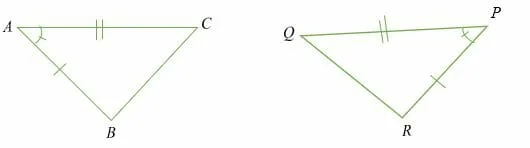
Given that; length AB = PR, AC = PQ and ∠ QPR = ∠ BAC, then; Triangle ABC and PQR are congruent (△ABC ≅△ PQR).

Angle – Angle – Side

The Angle – Angle – Side rule (AAS) states that two triangles are congruent if their corresponding two angles and one non-included side are equal.

Illustration:

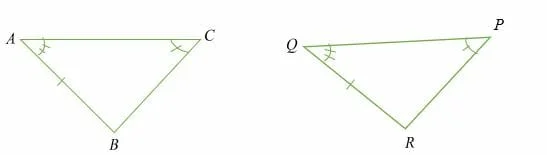
Given that;

∠ BAC = ∠ QPR, ∠ ACB = ∠ RQP and length AB = QR, then triangle ABC and PQR are congruent (△ABC ≅△ PQR).

Side – Side – Side

The side – side – side rule (SSS) states that: Two triangles are congruent if their corresponding three side lengths are equal.

Illustration:

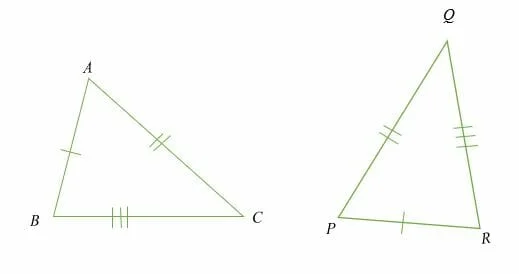
Triangle ABC and PQR are said to be congruent (△ABC ≅△ PQR) if length AB = PR, AC = QP, and BC = QR.

Angle – Side – Angle

The Angle – Side – Angle rule (ASA) states that: Two triangles are congruent if their corresponding two angles and one included side are equal.

Illustration:

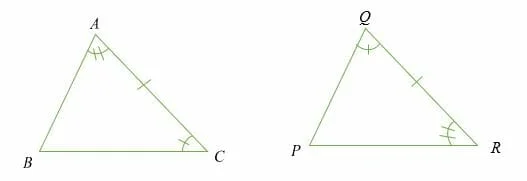
Triangle ABC and PQR are congruent (△ABC ≅△ PQR) if length ∠ BAC = ∠ PRQ, ∠ ACB = ∠ PQR.

Worked examples of triangle congruence:

Example 1

Two triangles ABC and PQR are such that; AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Check whether the triangles are congruent.

Solution

Given: AB = PR = 3.5 cm

BC = PQ = 7.1 cm and

AC = QR = 5 cm

Therefore, ∆ABC ≅ ∆PQR (SSS).

Example 2

Given that ∠ABC = (2x + 30) °, ∠PQR = 55 ° and ∠ RPQ = 65 °, find the value of x.

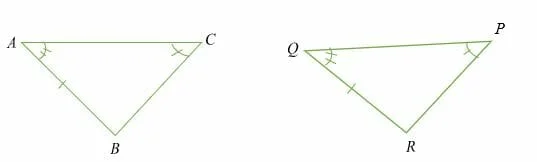
Solution

∆ABC ≅ ∆PQR

Therefore,

55 ° + 65 ° + (2x + 30) ° = 180°

120° + 2x + 30° = 180°

150° + 2x = 180°

2x = 30°

x = 15°

Example 3

Describe the type of congruence in two triangles given by;

∆ ABC, AB = 7 cm, BC = 5 cm, ∠B = 50° and ∆ DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°

Solution

Given:

AB = EF = 7 cm,

BC = DE = 5 cm and

∠B =∠E = 50°

Therefore, ∆ABC ≅ ∆FED (SAS)

Real-life examples of congruent objects (h3)

There are infinite examples of congruent objects which we see or observe in our daily life. A simple example is a pack of biscuits with all biscuits of the same size and shape if they are not broken. We can say all the biscuits are congruent.

A few more examples of congruency are:

• Earrings of the same set.

• Cigarettes in a pack.
• Wheels of a bicycle.
• Pages of a particular book.
• Your little fingers of both hands. Other fingers and thumbs are also congruent. Many of your body organs, like kidneys and lungs, are congruent. Even if a body is cut vertically from the center into two halves, both halves are congruent.