Hypotenuse Leg Theorem – Explanation & Examples

In this article, we’ll learn about the hypotenuse leg (HL) theorem. Like, SAS, SSS, ASA, and AAS, it is also one of the congruency postulates of a triangle.

The difference is that the other 4 postulates apply to all triangles. Simultaneously, the Hypotenuse Leg Theorem is true for the right triangles only because, obviously, the hypotenuse is one of the right-angled triangle legs.

What is Hypotenuse Leg Theorem?

The hypotenuse leg theorem is a criterion used to prove whether a given set of right triangles are congruent.

The hypotenuse leg (HL) theorem states that; a given set of triangles are congruent if the corresponding lengths of their hypotenuse and one leg are equal.

Unlike other congruency postulates such as; SSS, SAS, ASA, and AAS, three quantities are tested, with hypotenuse leg (HL) theorem, two sides of a right triangle are only considered.

Illustration:

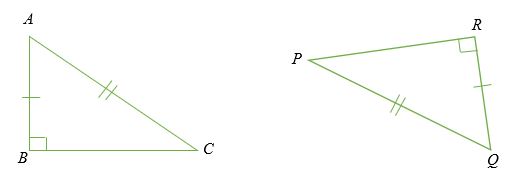
Proof of Hypotenuse Leg Theorem

In the diagram above, triangles ABC and PQR are right triangles with AB = RQ, AC = PQ.

By Pythagorean Theorem,

AC² = AB² + BC² and PQ² = RQ² + RP²

Since AC = PQ, substitute to get;

AB² + BC² = RQ² + RP²

But, AB = RQ,

By substitution;

RQ² + BC² = RQ² + RP²

Collect like terms to get;

BC² =RP²

Hence, △ABC ≅△ PQR

Example 1

If PR ⊥ QS, prove that PQR and PRS are congruent

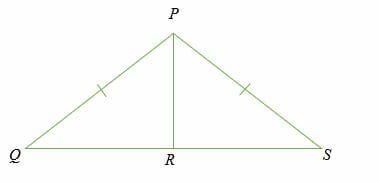
Solution

Triangle PQR and PRS are right triangles because they both have a 90-degree angle at point R.

Given;

• PQ = PS (Hypotenuse)
• PR = PR (Common side)
• Therefore, by Hypotenuse – Leg (HL) theorem, △ PQR ≅△ PR.

Example 2

If FB = DB, BA = BC, FB ⊥ AE and DB ⊥ CE, show that AE = CE.

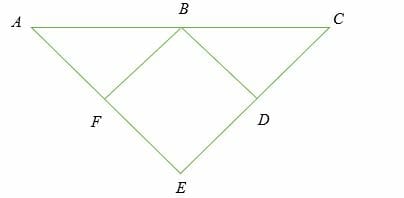
Solution

By Hypotenuse Leg rule,

• BA = BC (hypotenuse)
• FB = DB (equal side)
• Since, ∆ AFB≅ ∆ BDC, then ∠A = ∠ Therefore, AE = CE

Hence proved.

Example 3

Given that ∆ABC is an isosceles triangle and ∠ BAM = ∠MAD. Prove that M is the midpoint of BD.

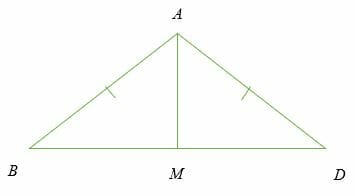
Solution

Given ∠ BAM = ∠MAD, then line AM is the bisector of ∠ BAD.

• AB = AD (hypotenuse)
• AM = AM (common leg)
• ∠ AMB = ∠AMD (right angle)
• Therefore, BM = MD.

Example 4

Check whether ∆XYZ and ∆STR are congruent.

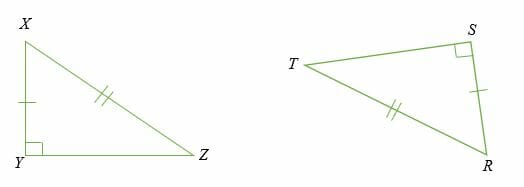
Solution

• Both ∆XYZ and ∆STR are right triangles (presence of a 90 – degree angle)
• XZ = TR (equal hypotenuse).
• XY = SR (Equal leg)
• Hence, by Hypotenuse-Leg (HL) theorem, ∆XYZ ≅∆STR.

Example 5

Given: ∠A=∠C = 90 degrees, AD= BC.  Show that △ABD ≅ △DBC.

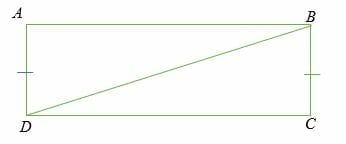
Solution

Given,

• AD = BC (equal leg)
• ∠A=∠C (right angle)
• BD = DB (common side, hypotenuse)
• By, by Hypotenuse-Leg (HL) theorem, △ABD ≅ △DBC

Example 6

Suppose ∠W = ∠ Z = 90 degrees and M is the midpoint of WZ and XY. Show that the two triangles WMX and YMZ are congruent.

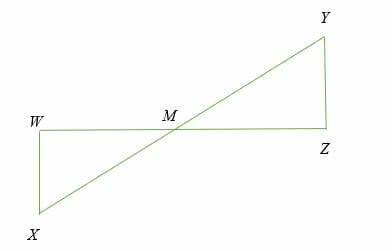
Solution

• △WMX and △YMZ are right triangles because they both have an angle of 90⁰ (right angles)
• WM = MZ (leg)
• XM = MY (Hypotenuse)
• Therefore, by Hypotenuse-Leg (HL) theorem, △WMX ≅ △YMZ.

Example 7

Calculate the value of x in the following congruent triangles.

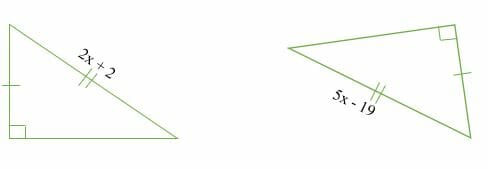
Solution

Given the two triangles are congruent, then;

⇒2x + 2 = 5x – 19

⇒2x – 5x = -19 – 2

⇒ -3x = – 21

x =- 21/-3

x = 7.

Therefore, the value of x = 7

Proof:

⇒ 2x + 2 = 2(7) + 2

⇒14 + 2 = 16

⇒ 5x -19 = 5(7) – 19

⇒ 35 – 19 = 16

Yes, it worked!

Example 8

If ∠ A = ∠ C = 90 degrees and AD = BC. Find the value of x and y that will make the two triangles ABD and DBC congruent.

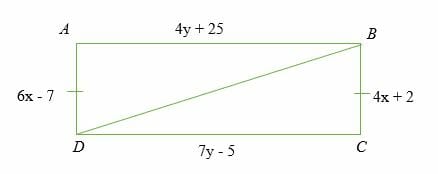
Solution

Given,

△ABD ≅ △DBC

Calculate the value of x

⇒ 6x – 7 = 4x + 2

⇒ 6x – 4x = 2 + 7

⇒ 2x = 9

⇒ x = 9/2

x = 4.5

Calculate the value of y.

⇒ 4y + 25 = 7y – 5

⇒ 4y – 7y = – 5 – 25

⇒ -3y = -30

y = -30/-3 =10

Therefore, △ABD ≅ △DBC, when x = 4.5 and y = 2.72.