Construct a 60 Degree Angle – Explanation and Examples

The easiest way to construct a 60-degree angle is to construct an equilateral triangle, which will have three angles with 60 degrees each.

The construction of an equilateral triangle was Euclid’s first proposition in book 1 of his Elements. Knowing how to construct one can also help us construct 120-degree angles, 30-degree angles, and 15-degree angles.

Before moving on with this section, it is a good idea to review the basics of construction. It is also a good idea to review the section on constructing line segments, as copying a line segment uses some of the same techniques.

In this topic, we will cover:

How to construct a 60 Degree Angle

How to Construct a 60 Degree Angle

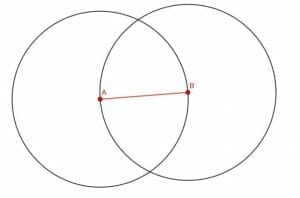
To construct a 60-degree angle, we first need to construct a line segment. Let’s call it AB. We can do this by picking two random points and then lining up our straightedge with those points. If we trace along the edge, we will have the segment AB.

Now, we need to use our compass to construct two circles. First, we place the point of the compass at B and the pencil tip at A. Then, holding the point in place, we can trace out the circumference of the circle by pivoting the compass around the point B. We can then do the same by placing the point at A and the pencil tip at B and tracing out a circumference by pivoting the compass.

Next, we denote either of the circles’ two intersections as C. We’ll use the top one, but it doesn’t matter. If we construct the lines AC and BC, we have an equilateral triangle.

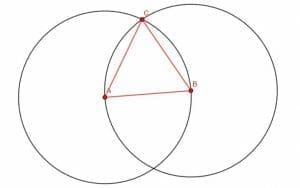
It is simple to prove that this is indeed an equilateral triangle.

Proof

AB is a radius of both circles. AC is a radius of the circle centered at A because it extends from the center to the circumference since all radii of a circle have the same length, AC=AB.

Likewise, BC is a radius of the circle B because it extends from the center to the circumference. Consequently, BC=AB.

Then, since AC=AB=BC, the transitive property tells us that AC=BC. Since the three line segments make up a triangle, the triangle must be equilateral.

Note on Measuring Angles

Recall that axiomatic geometry does not typically use measurements. Therefore, constructing a 60-degree angle is not exactly what we should call this angle.

Instead, we need to look at the angle relative to geometric objects. We could call it one-third of a straight line or one-third of two right angles. The first example will show a proof that one-third of a straight line is indeed equal to any angle in an equilateral triangle.

Examples

In this section, we will cover problems related to the construction of a 60-degree angle.

Example 1

Prove that an angle of an equilateral triangle is one-third of the measure of a straight line.

Example 1 Solution

It’s actually easiest to do this with a construction by showing that:

All of the angles in an equilateral triangle are equal, and
Three of these angles together form a straight line.

To prove the first part, let’s use some facts about isosceles triangles that Euclid proves in Elements 1.5. Namely, we will use the fact that angles at the base of isosceles triangles are the same.

Since the equilateral triangle has two sides the same, the angles at its base must also be the same. If we take AB to the base and AC, BC to be the equal sides, we know that CAB and CBA angles are the same.

If we consider AC to be the base and BC, AB to be the equal sides, then we note that the angles BCA and CAB are the same.

Since BCA=CAB=CBA, all three angles are equal.

For the second part of the proof, we will construct a straight line using three angles from an equilateral triangle.

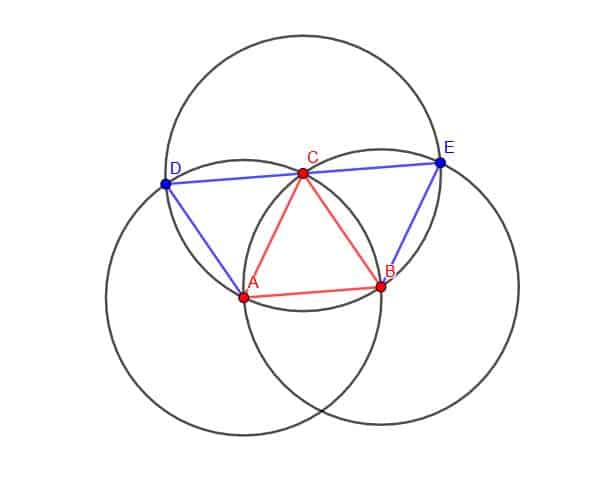
We do this by extending what we did to construct the equilateral triangle in the first place.

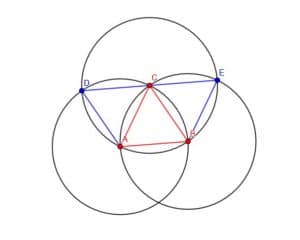
First, construct a circle with center C and radius CA. This circle will intersect both of the original circles at different points, which we will call D and E. Connect D to A and C, and then connect E to B and C.

Now, we have three equilateral triangles, ABC, BCE, and ACD.

In particular, the angles DCA, ACB, and BCE together form the straight line DE. Since each of these is an angle of an equilateral triangle and each angle is equal, each angle must be equal to one-third of a straight line.

Example 2

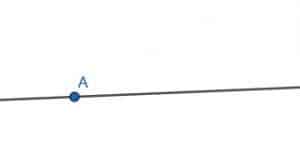
Construct a 60-degree angle at the point A on a line.

Example 2 Solution

This is actually easier to do than the general construction of a 60-degree angle.

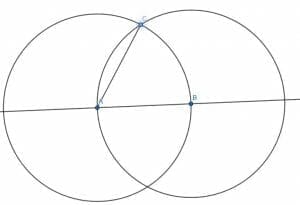
First, pick a random point B on the line in the direction you want to construct the angle. In this case, we will construct the angle, so it faces right.

Then, proceed as if you were making an equilateral triangle with AB as one of the legs. When you find the intersection of the two circles, C, however, construct AC. This will be equal to a 60-degree angle.

Example 3

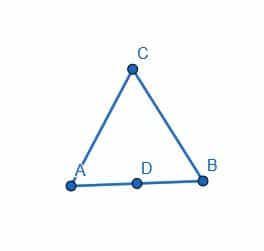
Construct a triangle with measures of 30, 60, and 90 degrees.

Example 3 Solution

Again, since construction doesn’t use measurements, we can also think of this as constructing a triangle with a right angle, an angle that is one-third of a straight line, and an angle that is one-sixth of a straight line.

There is an easy trick, though, that we can use to get a triangle like this.

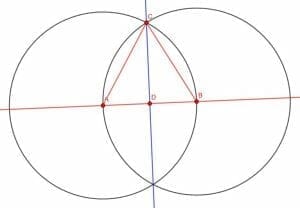
If we have an equilateral triangle and create a perpendicular bisector through AB at D, we will actually create the triangle we are looking for.

Such a perpendicular bisector will also bisect the angle ACB. This is because the angles CAB and CBA are equal, the segments AD and DB are equal, and AC is equal to BC. Euclid tells us Elements 1.4 that if two triangles have two sides equal and the angle in between equal, then the whole triangles are equal. Consequently, the angles DCB and DCA will be equal, meaning DC bisects ACB.

Since ACB was an angle in an equilateral triangle, DCB is half of that. This means it is 30 degrees or one-sixth of a straight line. Since DC is a perpendicular bisector, CDB is a right angle. Therefore, the triangle DCB has the required measurements.

Example 4

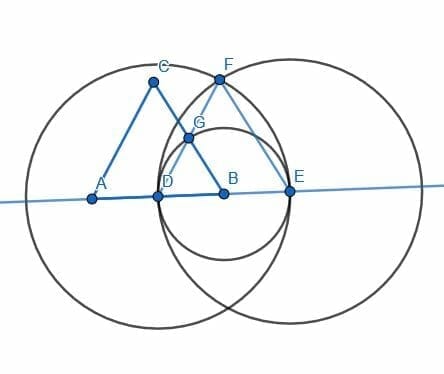
Construct a 120-degree angle.

Example 4 Solution

Constructing a 120-degree angle requires that we put two 60 degree angles together.

We can actually use the same construction used in example 1 to prove that the angles of an equilateral triangle were equal to one-third of a straight line.

In this case, the angle DAB consists of two smaller angles, DAC and CAB. Both of these angles, however, are angles in an equilateral triangle. Therefore, they are both 60 degrees, so the angle DAB will be 120 degrees. Using non-measurement terminology, we would say that it is two-thirds of a straight line.

Example 5

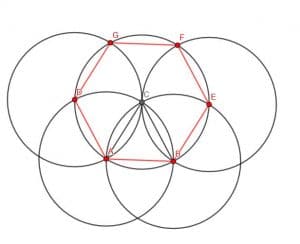
Construct a regular hexagon.

Example 5 Solution

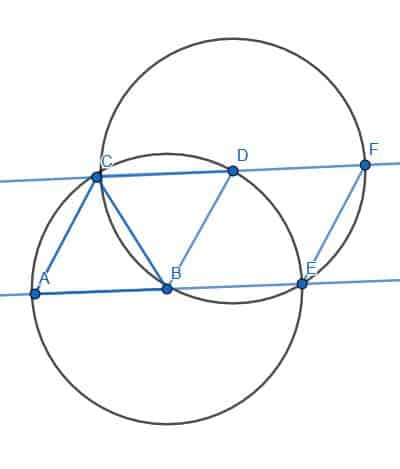
Hexagons have interior angles equal to 120 degrees. Therefore, we can extend the construction we used in examples 1 and 4 to create one.

We will have to construct an equilateral triangle ABC. Then, create a circle with center C and radius CA. We’ll label the intersection of this circle with the circle that has center A as D and the intersection with the circle that has center B as E.

Then, we can put the point of our compass and E and the pencil at C. We can then construct a new circle that has center E and radius EC. Likewise, we can construct a circle with center D and radius DC.

These circles will intersect the circle with center C. Let’s call the intersections F and G, respectively.

Now, we can connect BE, EF, FG, GD, and DA. These five lines, along with the original segment AB, will form a hexagon.