- Home
- >
- Constructing Perpendicular Bisector – Explanation & Examples
JUMP TO TOPIC
Constructing Perpendicular Bisectors – Explanation and Examples
 Constructing a perpendicular bisector with a compass and straightedge requires that we first find the center of a line segment and then construct a line perpendicular to that point.
Constructing a perpendicular bisector with a compass and straightedge requires that we first find the center of a line segment and then construct a line perpendicular to that point.
To do this requires constructing an equilateral triangle on the line segment.
Before moving on, review the construction of a perpendicular line.
In this section, we will go over:
- How to Construct a Perpendicular Bisector
- How to Construct a Perpendicular Bisector of a Given Line Segment
- How to Construct the Perpendicular Bisector of a Triangle
How to Construct a Perpendicular Bisector
A perpendicular bisector is a line that meets a given line segment at a right angle and cuts the given line segment into two equal halves.
Constructing such a line requires that we draw an equilateral triangle on the given line segment and then bisect the third vertex. Then, we extend the angle bisector so that it intersects the initial line. We can then prove that this line will meet the given line at its center and form a right angle.
How to Construct a Perpendicular Bisector of a Given Line Segment
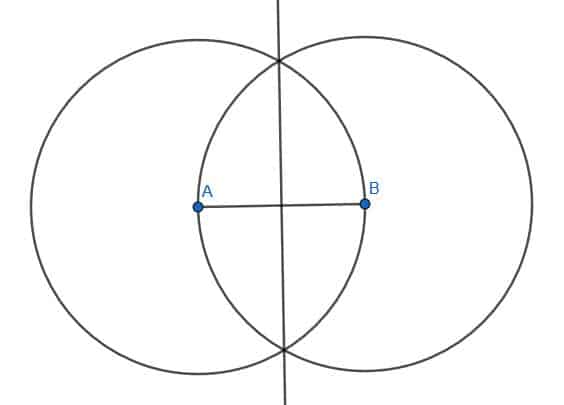
Suppose we are given a line segment AB. We want to construct a line that meets this segment at a right angle and divides the given segment into two equal parts.

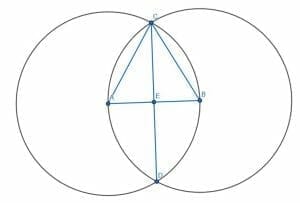
First, we draw two circles with length AB. The first will have center A, while the second will have center B. Label the intersection of these circles as C and draw segments AC and BC. The triangle ABC will be equilateral.
Then, we must bisect the angle ACB (how-to here). Call the intersection of the angle bisector and the line AB E.
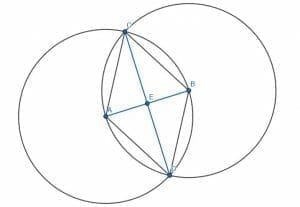
Proof of Perpendicular Bisector
We can first prove that E is the center of AB by showing that AE=BE.
AC=BC because they are both legs of an equilateral triangle, ACE=BCE because CE bisects ACB, and CE is equal to itself. Therefore, since the triangles, ACE and BCE, have two sides the same and the angle between those sides the same, the two triangles are congruent. This means that the third sides, namely AE and BE, are equivalent. Thus, E is the center of the segment AB, and CE bisects AB.
Since the two resulting angles, CEA and CEB, are congruent and adjacent, they are right angles. Therefore, CE is also perpendicular to AB.
How to Construct the Perpendicular Bisector of a Triangle
Perpendicular bisectors are useful for finding the circumcenter of a triangle. That is, we use them to find a point inside a triangle that is equidistant from each of the vertices.
To do this, we must construct a perpendicular bisector for each of the three legs of the triangle and draw it the whole way through the center of the triangle. The intersection of these three bisectors will be the circumcenter. This is true for any triangle, scalene, isosceles, or equilateral.
Examples
In this section, we will go over common example problems involving the construction of perpendicular bisectors.
Example 1
Find the center of the given line segment.

Example 1 Solution
First, we construct an equilateral triangle on the line segment AB by creating two circles with radius AB. The first will have center A, and the second will have center B. If we construct lines from A and B to the intersection of the circles, C, we will construct an equilateral triangle ABC.
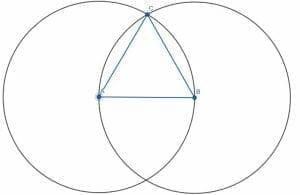
Then, we can construct a second equilateral triangle by connecting A and B to the other intersection of the circles, D. Finally, if we connect CD and label the intersection of CD and AB as E, we will have found the center of AB.
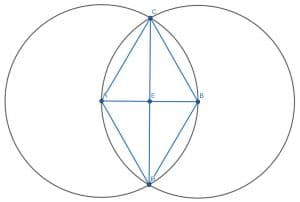
We know AE and BE are equal in length because the triangles ACE and BCE are congruent. This is because AC=BC, ACE=BCE, and CE are equal to themselves. Therefore, the triangles ACE and BCE are congruent, as are the sides AE and BE.
Example 2
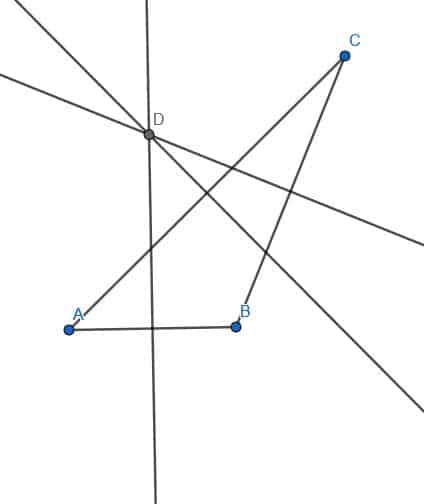
Construct a line perpendicular to the given line at point C.

Example 2 Solution
To do this, we first have to create a line segment that has C at its center. We can do this by constructing a circle with a radius equal to the shorter of AC and BC. In this case, BC is shorter. Then, label the intersection of this circle and the line AB as D.
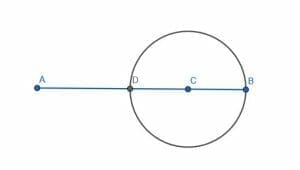
Now we can proceed as if we were constructing a perpendicular bisector on the segment DB. In this case, we already know the center point, but that doesn’t change our procedure much.
We still construct an equilateral triangle DBE. Then, we can connect EC.
We know that EC is still perpendicular because we know DE=BE as they are both legs of an equilateral triangle and EDC=EBC because they are both angles of an equilateral triangle. We also know that DC=BC since they are both radii of the circle with center C and radius BC. Therefore, the triangles EDC and EBC are equal, so the angles ECD and ECD are equal. By definition, since CE stands on the line DB and makes the adjacent angles equal, CE is perpendicular to DB.
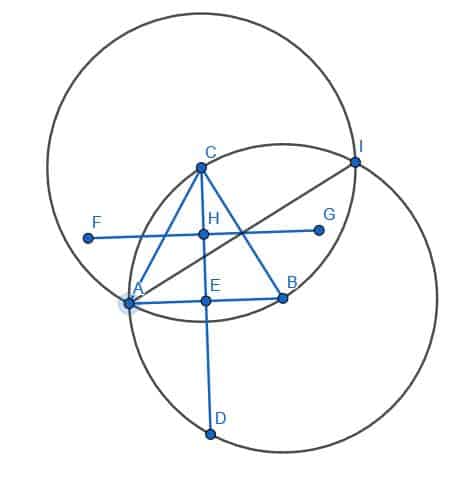
Example 3
Find the circumcenter of the given triangle.
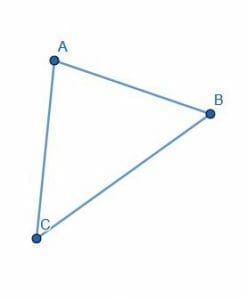
Example 3 Solution
Finding the circumcenter requires that we find a perpendicular bisector for each side of the triangle. Then, the point of intersection for these lines is the circumcenter or the point that is equidistant from each vertex.
We’ll begin with the side AB. As before, we draw two circles with radius AB, one with center A and one with center B. We can then take the “shortcut” and connect the two intersection points of these circles with a line DE. This will bisect the line AB.
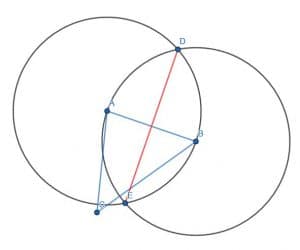
Next, we do the same for the line segments AC and BC.
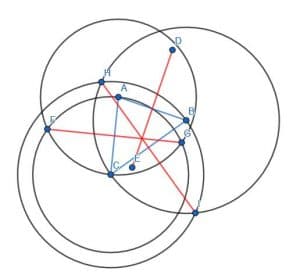
The intersection of these three lines, DE, FG, and HI, is the triangle ABC’s circumcenter.
Example 4
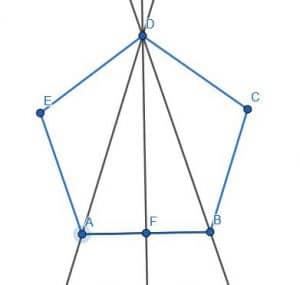
Divide the hexagon in half by connecting the center of two of its sides.
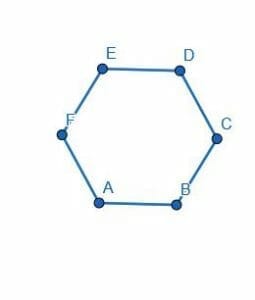
Example 4 Solution
The line segment we choose does not matter because each of the line segments has the same length.
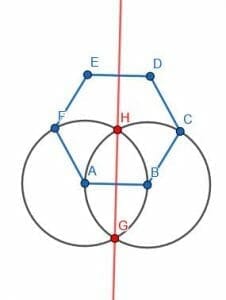
We’ll choose AB and construct a perpendicular bisector, HG. Then, we extend HG so that it hits another segment on the hexagon. The two halves are equal because of DC=EF, CB=FA. Then, if we call the center of ED I and the center of AB J, EI=DI, JA=JB, and IJ is equal to itself.
Example 5
Bisect the line segment shown by constructing an equilateral triangle, ABC, on AB. Then, construct a perpendicular bisector for the line segment connecting C and the center of AB. 
Example 5 Solution
We begin by bisecting the segment AB as before. We construct an equilateral triangle ABC and then bisect the angle ACB. The intersection of the angle bisector, which we call CD, and the segment AB, is E, the center of AB. Thus, CE is the perpendicular bisector of AB.
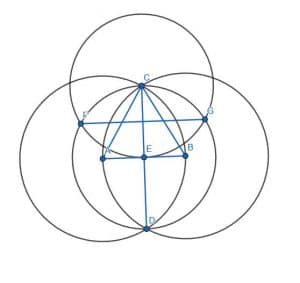
Now, we want to construct a perpendicular bisector for CE. We do the same thing, constructing two circles with radius CE. One will have center C, and the other will have center E. Then, we connect the two intersections of these circles, which we call F and G. The intersection of CE and FG is the center of CE. Therefore, FG is a perpendicular bisector to the perpendicular bisector.
Practice Questions
![]()
Open Problems
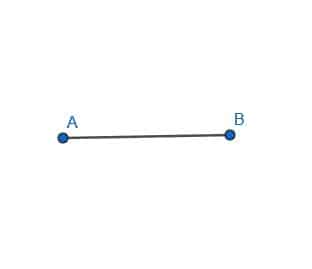
- Create a perpendicular bisector for the line segment AB.

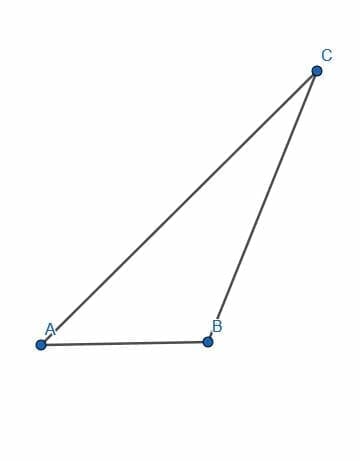
- Find the circumcenter of the triangle ABC.

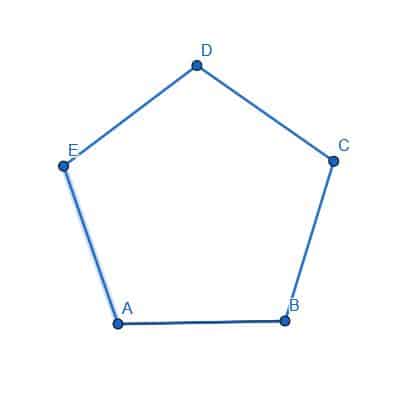
- Prove that the angle bisector of EDC cuts the pentagon ABCDE into two equal halves.

- Is the intersection of FG and CE in example 5 the circumcenter of the triangle ABC? Why or why not?
Open Problem Solutions
The angle bisector DF cuts the pentagon in half. AD=BD, ADF=BDF, and DF are equal to themselves. Therefore triangle ADF=BDF. Likewise, ED=BC, CDB=EDA, and AD=BD. Thus, the triangles BCD and AED are also equal.
4.
No, because the perpendicular bisector for BC does not pass through the point H.