Coplanar Lines – Explanations & Examples

Determining whether two or more lines are coplanar lines will be helpful, especially when working with basic and coordinate geometry. Let’s go ahead and recall its definition.

                                      Coplanar lines are lines that lie on the same plane.

If coplanar points are points that lie along the same plane, then the same applies for coplanar lines: they lie also share the same plane.

In this article, we’ll dive into the fundamental definition of coplanar lines, their properties and learn how we can identify them from real-world examples.

What are coplanar lines?

Lines and line segments that lie on the same plane (and consequently space) are considered coplanar lines.

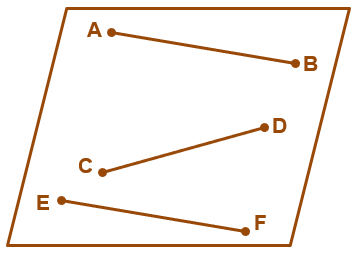The image above is a good example of a plane with three line segments coplanar to each other. $\overline{AB}$, $\overline{CD}$, and $\overline{EF}$ all lie on the same plane; that’s why they are coplanar lines.Let’s break down the important terms as well when learning about coplanar lines:

• line: a set of points that extend on both sides infinitely
• coplanar: when points or lines lie on the same plane, they are considered coplanar
• noncoplanar: when points or lines do not lie on the same plane, they are considered noncoplanar

What do we call lines that do not lie on the same plane? Lines that are not found on the same plane are called noncoplanar lines.

What are some real-world examples of coplanar lines?

• The lines on a notebook are coplanar to each other.
  • Since they lie on the same page, they lie on the same plane. Fun fact: not only are these lines coplanar, but they are also parallel.
• The hands-on of our watches and clocks are coplanar as well.
  • The second, minute, and hour hands all lie in the same circular space.
• The grids found on a graphing paper.
  • Since both the vertical and horizontal lines of the grid lie on the same paper, they are coplanar points.

How to find coplanar points and coplanar lines?

When looking for coplanar points and lines, it’s important to go back to the two’s basic definitions. Here’s a question guide to help you decide whether two or more points or lines are coplanar to each other:

• Do the lines lie on the same plane?
• Do the points lie on the same line?

If the answer is yes to either of the two questions, then they are coplanar. Start with a reference point or line, then look for another pair that lies along the same plane.

Coplanar lines definition

As a recap, lines are coplanar as long they share the same space and plane. In polygons, all its lines are coplanar with respect to each other.Let’s try looking for two pairs of coplanar points and coplanar lines from the figures shown below.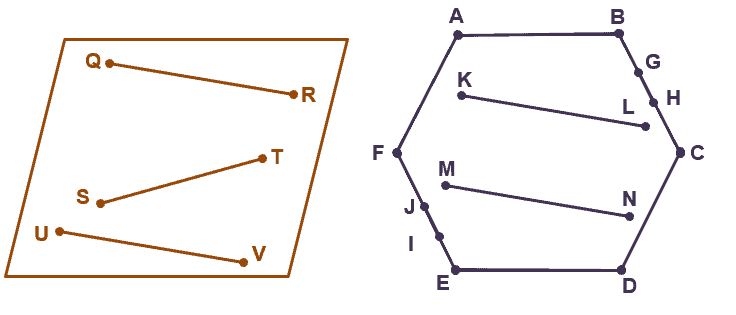When given a starting point, look out for points that lie along the same plane. Since we’re working with a two-dimensional figure, all points that lie on one plane are coplanar to each other.$Q$ and $R$ are coplanar.$K$ and $L$ are coplanar.Do the same for coplanar lines: lookout for a line that lies along the same plane.$\overline{ST}$ and $\overline{UV}$ are coplanar.$\overline{KL}$ and $\overline{MN}$ are coplanar.There are many other possible combinations so that you can give it a try on your own!Let’s try to answer the examples shown below using the properties we’ve just learned.

Coplanar lines in vector and coordinate geometry

We will be reintroduced to coplanar lines when we take advanced math classes involving equations in vector and cartesian forms.

• In vector form: If two nonparallel lines, $\boldsymbol{r} = \boldsymbol{a} + m\boldsymbol{b}$ and $\boldsymbol{r} = \boldsymbol{c} + n\boldsymbol{d}$ are coplanar, $(\boldsymbol{c}-\boldsymbol{a})(\boldsymbol{b}\times\boldsymbol{d} = 0)$.
• In cartesian form: When the coefficients and their corresponding ratios’ determinant is zero, the lines are coplanar.

These are just a quick glimpse of how coplanar lines are applied in higher mathematics, but for now, let’s focus on the geometric definition and properties of coplanar points and lines.Let’s try to check our knowledge of coplanar points and lines by trying these examples.Example 1Which of the following are not coplanar?

1. Line marks on a compass.
2. Linear designs on a wallpaper.
3. Coordinates on an $xy$-plane.
4. The lines on two different notebooks.

SolutionThe first three choices all lie on the same plane.

• The compass contains all the line marks on one surface.
• Wallpapers are two-dimensional, so all the lines around and within it are coplanar.
• Coordinates on one plane are all coplanar points.

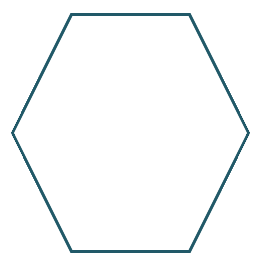However, the lines on two different notebooks lie on two different surfaces, so they are not coplanar.Example 2True or False? Skew lines are coplanar. Justify your answer.SolutionThis statement is false. Recall that skew lines are lines that do not lie on the same plane, never intersect, or parallel. This means that skew lines are never coplanar and instead are noncoplanar.Example 3Take a screenshot or snippet of the figure shown below, then draw two coplanar lines.

Solution

Since we’re working on a two-dimensional figure, we can construct coplanar lines around and within the figure. Here are some possible answers to this problem:

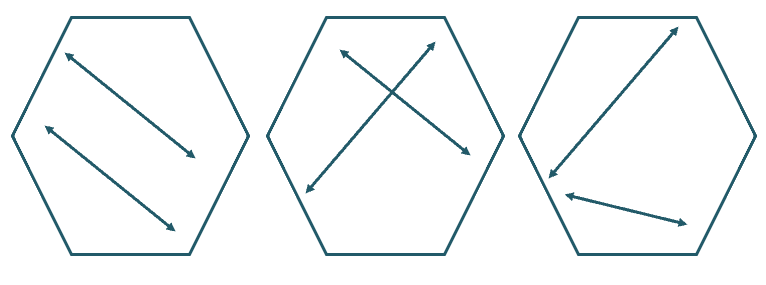
As you can see, as long as the lines are found within or around the hexagon, the solution will be considered valid. Now, time to work on your own and try to construct some coplanar lines!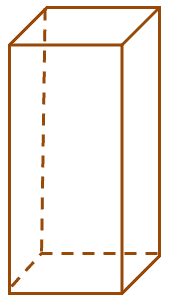

Example 4

Take a screenshot or snippet of the figure shown below, then draw two coplanar lines.

Solution

Since we’re working on a three-dimensional figure, we can construct coplanar lines around and within one surface at a time. Here are some possible answers to this problem:

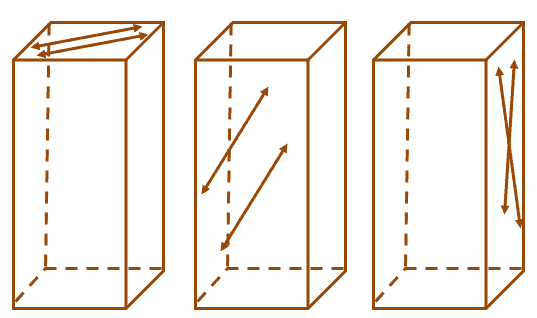
As you can see, as long as the lines are found within one surface each time, the pair of coplanar lines are valid.

There are six surfaces on the prism shown, so you’ll definitely be able to find other coplanar lines!

 Use the image shown below to answer Examples 5 to 6.

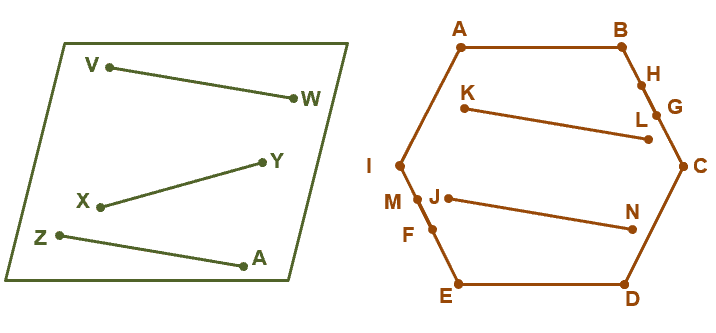
Example 5

Use the image shown above and name three pairs of coplanar points.

Solution

Recall that coplanar points are points that lie along the same plane. We can choose three pairs from either of the two planes as long as they are from the same plane each time.

Below are three possible pairs of coplanar points:

Points $A$ and $Z$

Points $M$ and $F$

Points $J$ and $N$

Example 6

Use the same image shown above and name three pairs of coplanar lines.

Solution

Recall that coplanar lines are lines that lie along the same plane. We can choose three pairs from either of the two planes as long as they are from the same plane.

Below are three possible pairs of coplanar lines:

Lines $\overline{ZA}$ and $\overline{VW}$

Lines $\overline{JN}$ and $\overline{KL}$

Lines $\overline{HG}$ and $\overline{CD}$

Use the image shown below to answer Examples 7 to 8.

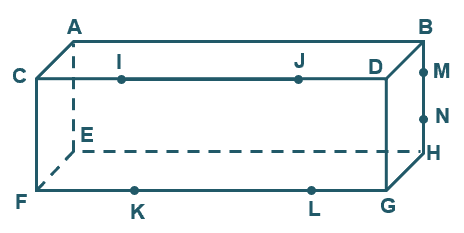Example 7Use the image shown above and name two sets of three coplanar points.SolutionRecall that coplanar points are points that lie along the same plane. To ensure that the points are coplanar, work on only one of the six surfaces from the rectangular prism.Let’s work on the front plane and name our first set of coplanar points. We can see eight possible points, so this means there can be multiple combinations for your answer.Two examples from the front are:Points $I$, $J$, and $L$Points $J$, $C$, and $F$We can also try looking for two sets from the right-hand side:Points $M$, $N$, and $H$Points $D$, $B$, and $G$Example 8Use the image shown above and name two sets of three coplanar lines.SolutionRecall that coplanar lines are lines that lie along the same plane. Work on only one of the six surfaces from the rectangular prism each time we name a set.As from the previous example, it is ideal that we focus on one surface each time we name a set of three coplanar lines. This, let’s try to find two sets from the surface on the back. We have:Lines $\overline{IJ}$, $\overline{DG}$, and $\overline{KL}$Lines $\overline{FK}$, $\overline{CF}$, and $\overline{JD}$We can also try looking for two sets from the right-hand side:Lines $\overline{DB}$, $\overline{DG}$, and $\overline{BH}$Lines $\overline{MN}$, $\overline{NG}$, and $\overline{HG}$Your answers may differ from the ones shown, but as long as they meet the conditions, they should be valid.