Critical numbers – Definition, Process, and Examples
Knowing how to find a function’s critical numbers will come in handy when we want to determine extreme values and quantities. Finding critical numbers is a helpful optimization technique applied in physics, finance, and engineering as well.
Critical numbers are values of a function where the function’s tangent lines are either horizontal or vertical.
In this article, we’ll focus on critical numbers that return values of $x$ where $f’(x)$ is either zero or an undefined value. We’ll also learn how to identify them and understand what these points represent.
What are critical numbers?
Critical numbers or critical points are values of $x$ where the first derivative of a function is either equal to zero or undefined. Let’s say we have $x = c$, the critical numbers of the function,$f(x)$, will satisfy either of the following:
\begin{aligned}f’(c) &= 0 \\\\f’(c) &= \text{ DNE (Does Not Exist)}\end{aligned}
This means that $x =c$ is a critical number when a tangent line passing through $\boldsymbol{x = c}$ is either a horizontal or vertical line.
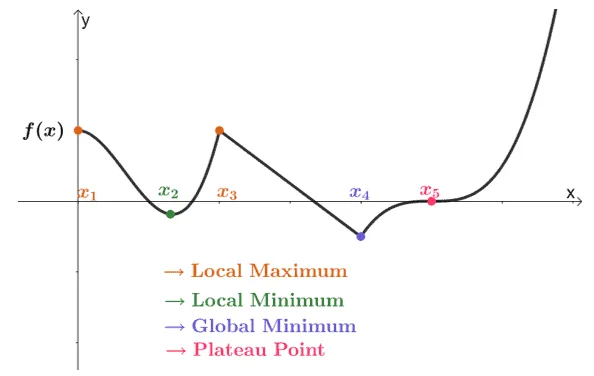
The graph above shows us examples of critical numbers meeting different conditions. Let’s break down what each critical number represents:
- The local extremums (both minimum and maximum) indicate the extremum value within an interval.
- The global extremum tells us the definite maximum or minimum value of the function throughout its domain.
- Points where the function “plateau” or inflect tells us that the derivative changes from increasing to decreasing (or the other way around).
All these components will only be considered critical points of the function when the first derivative is either zero or doesn’t exist.
How to find critical numbers?
We can use the definition of critical numbers to determine the critical numbers – by finding the values of $x$ where $f’(x) = 0$ or $f’(x) = \text{ DNE}$. These are some guide points to help you find a function’s critical numbers:
- Use the derivative rules to find $f’(x)$’s expression.
- Find the values of $x$ where $f’(x) = 0$.
- Include the values of $x$ where $f’(x)$ is undefined.
Only include critical numbers that are within the function’s domain. This means that values of $x$ where $f’(x)$ is undefined will only count when the point is within the domain of $f(x)$.
Now, take a look at this graph and observe how these critical numbers would appear on an $xy$-coordinate system.
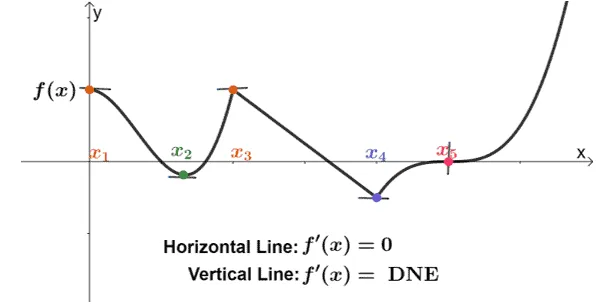
When given the graph of $f(x)$, we can inspect the points where the tangent line passing through $f(x)$ is either vertical or horizontal.
- When the tangent line at $x = c$ is vertical, $f’(c) = 0$ and we have critical point at $x = c$.
- Similarly, when the tangent line passing through $x = c$ is horizontal, $f’(c)$ is undefined and $x=c$ is also a critical point.
Let’s use these techniques and tips to find the critical numbers of the functions shown below.
Example 1
What are the critical numbers of the function, $f(x) = 2x^3 – 8x^2 + 2x – 1$?
Solution
We can determine the critical numbers of $f(x)$ by first finding the expression for $f(x)$’s derivative.
- Use the sum and difference rules to distribute $\dfrac{d}{dx}$ throughout each term.
- Factor out the coefficient by applying the constant multiple rule.
- Use the power rule to simplify the terms of $f’(x)$.
\begin{aligned}f(x) &= 2x^3 – 8x^2 + 2x – 1\\f'(x) &= \dfrac{d}{dx}2x^3 – \dfrac{d}{dx}8x^2 + \dfrac{d}{dx}2x – \dfrac{d}{dx}1,\phantom{x}{\color{Orchid} \text{Sum and Difference Rules}}\\&= {\color{Orchid}2\dfrac{d}{dx}x^3} – {\color{Orchid}8\dfrac{d}{dx}x^2} + {\color{Orchid}2\dfrac{d}{dx}x }- {\color{DarkOrange} 0},\phantom{x}{\color{Orchid} \text{Constant Multiple Rule}}\text{ & }{\color{DarkOrange} \text{Constant Rule}}\\&= 2({\color{Orchid}3x^2 })-8({\color{Orchid}2x })+2({\color{Orchid}1 }),\phantom{x}{\color{Orchid} \text{Power Rule}}\\&= 6x^2 – 16x + 2\end{aligned}
Recall that critical numbers occur at values of $x$ when $f’(x) = 0$ or when $f’(x)$ does not exist. Since $f’(x)$ is a quadratic expression, $x$ has no restrictions. Equate $f’(x)$ to zero to find the critical numbers instead.
\begin{aligned}f'(x) &= 0\\ 6x^2 – 16x + 2 &=0 \\3x^2 – 8x + 1 &= 0\end{aligned}
Since we can’t factor the quadratic expression, we can use the quadratic formula to determine the critical numbers of $f(x)$ instead.
\begin{aligned}x&= \dfrac{-(-8) \pm \sqrt{(-8)^2 – 4(3)(1)}}{2(3)}\\&= \dfrac{8 \pm \sqrt{64 – 12}}{6}\\&= \dfrac{8 \pm \sqrt{52}}{6}\\&=\dfrac{8 \pm 2\sqrt{13}}{6}\\&=\dfrac{4 \pm \sqrt{13}}{3}\end{aligned}
This means that $f(x)$ has critical numbers at $x = \dfrac{4 \pm \sqrt{13}}{3}$.
The graph of $f(x) = 2x^3 – 8x^2 + 2x – 1$ is shown below for you to understand what these critical numbers represent.
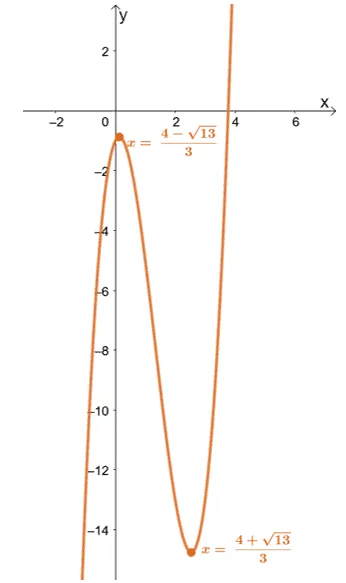
We can see that both critical numbers are considered $f(x)$’s local minima and the tangent lines passing through them will be horizontal.
Example 2
What are the critical numbers of the function, $g(x) = \dfrac{x^2 – 6}{x -4}$?
Solution
We begin by differentiating $g(x)$ and to do so, we’ll apply the following derivative rules.
- Since $g(x)$ is a rational expression, we’ll apply the quotient rule
- Apply the constant and power rules whenever necessary.
\begin{aligned}g(x) &= \dfrac{x^2 – 6}{x -4}\\g'(x) &= \dfrac{(x- 4)\dfrac{d}{dx} (x^2 -6) – (x^2 – 6)\dfrac{d}{dx}(x – 4)}{(x – 4)^2},\phantom{x}{\color{Orchid}\text{Quotient Rule}}\\&= \dfrac{(x- 4){\color{Orchid}\left(\dfrac{d}{dx}x^2 -\dfrac{d}{dx}6\right)} – (x^2 -6){\color{Orchid}\left(\dfrac{d}{dx}x – \dfrac{d}{dx}4\right)}}{(x – 4)^2},\phantom{x}{\color{Orchid}\text{Difference Rule}}\\&=\dfrac{(x- 4)({\color{Orchid}2x} – {\color{DarkOrange}0})- (x^2 – 6)({\color{Orchid}1} – {\color{DarkOrange}0})}{(x – 4)^2},\phantom{x}{\color{Orchid}\text{Power Rule}}\text{ & }{\color{DarkOrange}\text{Constant Rule}}\end{aligned}
Expand the terms in the numerator and combine the terms whenever possible to simplify $g’(x)$.
\begin{aligned}g'(x) &= \dfrac{2x(x -4) – (x^2 – 6)}{(x -4)^2}\\&= \dfrac{2x^2 – 8x – x^2 +6}{(x -4)^2}\\&= \dfrac{x^2 – 8x +6}{(x -4)^2}\end{aligned}
We can find the critical numbers of $g(x)$ by equating $g’(x)$ to zero or by finding undefined values within its domain. For $g’(x)$ to be undefined, the denominator must be zero.
\begin{aligned}(x – 4)^2 &= 0 \\x &= 4\end{aligned}
It may be tempting to include $x = 4$ as one of $g(x)$’s critical numbers, but keep in mind $x = 4$ is not part of $g(x)$’s domain. Hence, we disregard it.
Let’s now focus on the values of $x$ that returns $g’(x) = 0$. After equating the numerator to $0$, apply the quadratic formula to find $x$.
\begin{aligned}g'(x) &=0\\ \dfrac{x^2 – 8x +6}{(x -4)^2}&= 0\\x^2 – 8x + 6 &= 0\\x&= \dfrac{-(-8) \pm \sqrt{(-8)^2 – 4(1)(6)}}{2(1)}\\&=\dfrac{8 \pm \sqrt{64 -24}}{2}\\&=\dfrac{8 \pm 2\sqrt{10}}{2}\\&= 4 \pm \sqrt{10}\end{aligned}
This means that $g(x)$ has critical numbers at $x = 4 – \sqrt{10}$ and $x = 4 + \sqrt{10}$.
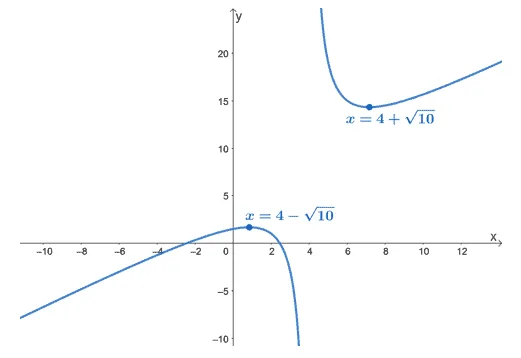
Here’s the graph of $g(x)$ to show you where the critical numbers are located. From this, we can see that $x = 4 – \sqrt{10}$ is a local maximum while $x = 4+\sqrt{10}$ is a local minimum.
Practice Questions
1. What are the critical numbers of the following functions?
a. $f(x) = 2x^4 – 5x^3 – 6x^2$
b. $g(x) = -5x^3 – 4x^2 + 12$
c. $h(x) = 12x^6 – 8x^4 + 202$
2. What are the critical numbers of the following functions?
a. $f(x) = \dfrac{x – 1}{x^2 + 4}$
b. $g(x) = \dfrac{x^2 – 3}{x – 2}$
c. $h(x) = (x +3)^2 (x -2)$
Answer Key
1.
a. $x = \left\{\dfrac{-15 -\sqrt{609}}{3}, 0 ,\dfrac{15 – \sqrt{609}}{3} \right\}$
b. $x=\left\{-\dfrac{18}{5},0\right\}$
c. $x=\left\{-\dfrac{2\sqrt{3}}{3}, 0, \dfrac{2\sqrt{3}}{3}\right\}$
2.
a. $x = \{1 – \sqrt{5}, 1 + \sqrt{5}\}$
b. $x = \{1, 3\}$
c. $x=\left\{-3, \dfrac{1}{3}\right\}$
Images/mathematical drawings are created with GeoGebra.