- Home
- >
- Cylindrical Coordinates – Definition, Graph, and Examples
JUMP TO TOPIC
Cylindrical Coordinates – Definition, Graph, and Examples
The cylindrical coordinates show us how we can extend our knowledge of polar coordinates in a three-dimensional coordinate system. Using the cylindrical coordinate system allows us to work with problems that involve cylinders.
The cylindrical coordinate system is an extension of the polar coordinates in the three-dimensional coordinate system. This means that the polar coordinates depend on three components: two distances and one polar angle.
Our discussion will cover all the fundamentals we need to learn about cylindrical coordinates. We’ll also show you how the polar coordinates are closely related to the cylindrical coordinates and we’ll also discuss cover the following:
- Converting cylindrical coordinates to rectangular coordinates and vice-versa.
- Finding and graphing cylindrical coordinates.
For now, let’s dive right into the definition of cylindrical coordinates to start mastering this topic!
What Are Cylindrical Coordinates?
The cylindrical coordinates represent points, $(r, \theta, z)$, lying on a three-dimensional coordinate system defined by the polar coordinates ($(r, \theta)$) of the point projected on the $xy$-plane and the distance ($z$) between the point and the $xy$-plane.
In the past, we’ve learned that the polar coordinate, $(r, \theta)$, represents two components: $r$ defines the distance of the point from the origin and $\theta$ represents the angle formed by the line segment connecting the point and the $x$-axis.
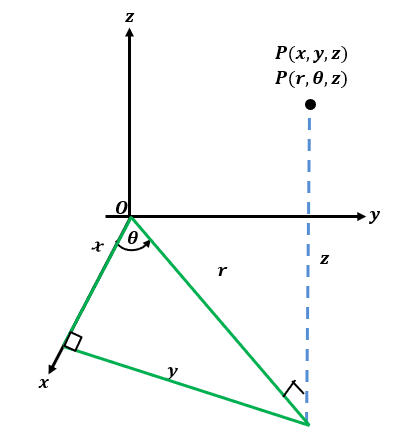
We can extend this 2D representation to the 3D coordinate system by projecting the polar coordinate on the $xy$-plane and accounting for the third axis: the $z$-axis. Hence, the cylindrical coordinate is represented by the triple coordinate, $(r, \theta, z)$. The graph shown above highlights how the cylindrical coordinate looks like on the 3D rectangular coordinate system.
Coordinate | Definition | Range |
\begin{aligned}r\end{aligned} | · radial distance · represents the distance of the point from the origin | \begin{aligned} 0 \leq r < \infty \end{aligned} |
\begin{aligned}\theta\end{aligned} | · polar angle · represents the angle formed by the $x$-axis and the line segment connecting $P$ and the origin | \begin{aligned} 0 \leq \theta \leq 2\pi \end{aligned} |
\begin{aligned}z\end{aligned} | · $z$-coordinate · represents the vertical height of the point | \begin{aligned} -\infty \leq z \leq \infty \end{aligned} |
There are infinite number of angles that can represent $\theta$ and this is why we’re limiting its range to $[0, 2\pi]$. Since $r$ represents the distance, it will always be positive, so disregard the negative roots when finding the value of $r$.
Now that we understand the fundamental components of the cylindrical coordinate system, it’s time that we learn how they relate to the rectangular coordinates.
How To Convert To Cylindrical Coordinates?
Converting rectangular coordinates to cylindrical coordinates is straightforward – we simply use the polar coordinate’s relationship with the rectangular coordinate. The value of $z$ remains the same.
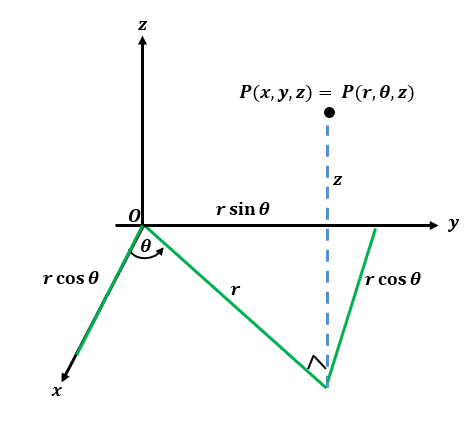
We’ll summarize the relationships between these two coordinate systems for you:
Cylindrical Coordinate To Rectangular Coordinate | Rectangular Coordinate To Cylindrical Coordinate |
\begin{aligned}x&= r\cos \theta\\y &= r\sin \theta\\z&= z\end{aligned} | \begin{aligned}r &= \sqrt{x^2 + y^2}\\ \theta &= \tan^{-1} \left(\dfrac{y}{x}\right)\\z &= z \end{aligned} |
This means that we can find the rectangular form of the cylindrical coordinate, $\left(3, \dfrac{\pi}{4}, 2\right)$, using the formula at the left column. Hence, we have the following coordinates:
\begin{aligned}r&= 3\\\theta&= \dfrac{\pi}{4}\\z&= 2\\\\x&= 3\cos \dfrac{\pi}{4}\\&=\dfrac{3\sqrt{2}}{2}\\y &= 3\sin \dfrac{\pi}{4}\\&= \dfrac{3\sqrt{2}}{2}\\z&= 2\end{aligned}
Hence, the rectangular coordinate of $\left(3, \dfrac{\pi}{4}, 2\right)$ is equal to $\left(\dfrac{3\sqrt{2}}{2}, \dfrac{3\sqrt{2}}{2}, 2\right)$. We’ll show you another example, but this time, we’ll convert $(1, 1, 2)$ to cylindrical coordinate as shown below.
\begin{aligned}x&= 1\\y&=1 \\z &= 2\\\\r &= \sqrt{1^2 + 1^2}\\&= \sqrt{2}\\ \theta &= \tan^{-1} \left(\dfrac{1}{1}\right)\\&= \dfrac{\pi}{4}\\z &= 2 \end{aligned}
This shows that $(1, 1, 2)$ is equal to $\left(\sqrt{2}, \dfrac{\pi}{4}, 2\right)$ in cylindrical coordinates. Apply a similar process when converting rectangular coordinates to cylindrical coordinates, and vice-versa.
How To Find Cylindrical Coordinates?
We can find the cylindrical coordinate’s position by using its rectangular form. We’ve broken down the steps for you here:
- Convert $(r, \theta, z)$ to its rectangular form: $(r, \theta, z) = (r\cos\theta, r\sin\theta, z)$.
- Use the rectangular form to locate the position of the cylindrical coordinate:
- Move $x$ units along the $x$-axis.
- From the position along the $x$-axis, move $y$ units parallel to the $y$-axis.
- The point’s height will depend on the $z$-component.
Use the guideline to locate the cylindrical coordinate’s position and you can a similar process to plot cylindrical coordinates. For example, if we want to locate the position of $\left(6, \dfrac{\pi}{3}, 4\right)$, we’ll convert the point to its rectangular form first:
\begin{aligned}r&= 6\\\theta&= \dfrac{\pi}{3}\\z&= 4\\\\x&= 6\cos \dfrac{\pi}{3}\\&=3\\y &= 6\sin \dfrac{\pi}{3}\\&= 3\sqrt{3}\\z&= 4\end{aligned}
This means that $\left(6, \dfrac{\pi}{3}, 4\right)$ is equivalent to $(3, 3\sqrt{3}, 4)$. We can use this to determine the position of the point:
- Move $3$ units along the $x$-axis.
- From the $x$-axis, move $3\sqrt{3} \approx 5.20$ units parallel to the positive $y$-axis’s direction.
- Project the point so that it is $4$ units above the $xy$-plane.
We can also plot the cylindrical point using its rectangular form’s position as shown below.
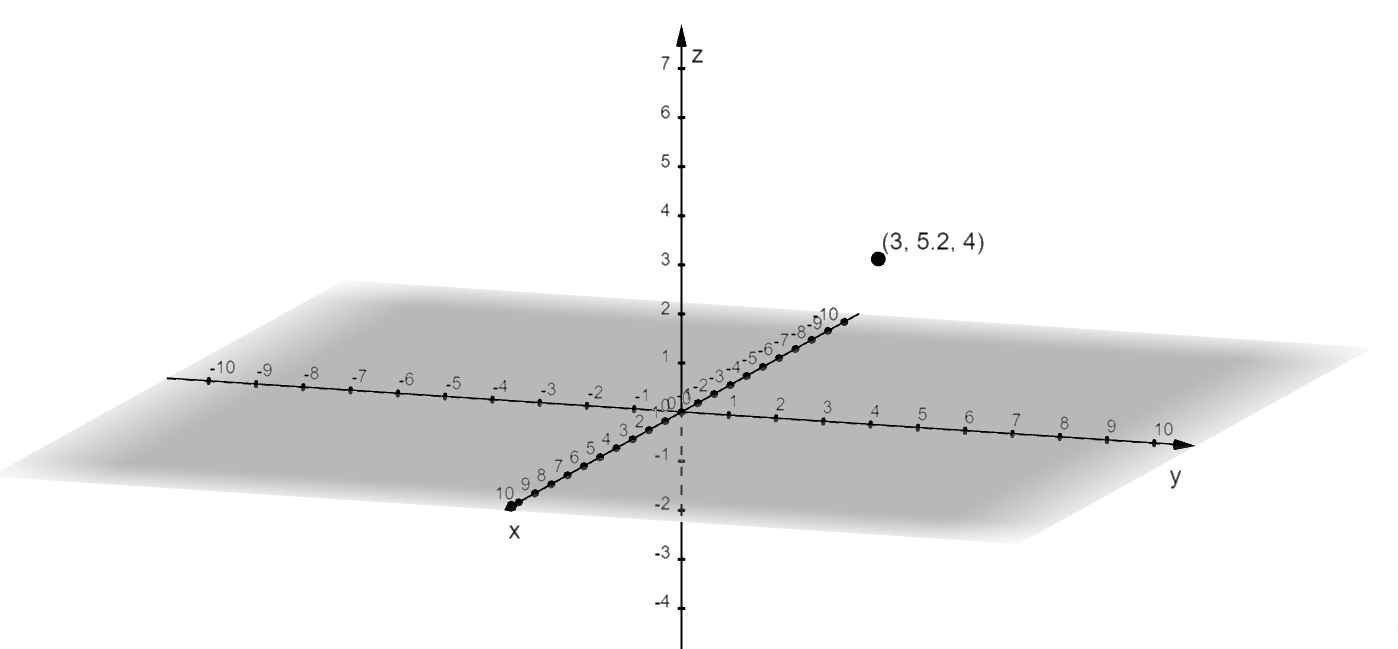
This shows that it is important that we know how to convert cylindrical coordinates to their rectangular forms in order for us to easily graph the point on the three-dimensional coordinate system.
Example 1
Convert the rectangular coordinate, $(2, 1, -4)$, to its cylindrical form.
Solution
We can use the following formulas to convert the rectangular coordinate to its cylindrical form as shown below.
\begin{aligned}r &= \sqrt{x^2 + y^2}\\ \theta &= \tan^{-1} \left(\dfrac{y}{x}\right)\\z &= z \end{aligned}
Using $x =2$, $y = 1$, and $z = -4$, we have the following:
$\boldsymbol{r}$ | \begin{aligned}r &= \sqrt{2^2 + 1^2}\\&= \sqrt{5} \end{aligned} |
$\boldsymbol{\theta}$ | \begin{aligned}\theta &= \tan^{-1} \left(\dfrac{1}{2}\right)\\&\approx 26.57^{\circ} \end{aligned} |
$\boldsymbol{z}$ | \begin{aligned}z &= -4 \end{aligned} |
This means that $(2, 1, -4)$ is equivalent to $(\sqrt{5}, 26.57^{\circ}, -4)$ in cylindrical form.
Example 2
Convert the cylindrical coordinate, $\left(6, \dfrac{2\pi}{3}, -3\right)$, to its rectangular form.
Solution
We’re now given the cylindrical coordinate and we need to convert them to rectangular coordinates, so we’ll use the following relationships:
\begin{aligned}x&= r\cos \theta\\y &= r\sin \theta\\z&= z\end{aligned}
We have $r= 6$, $\theta = \dfrac{2\pi}{3}$, and $z = -3$, so substitute these values into the three equations to find the Cartesian or rectangular form of the coordinate.
$\boldsymbol{x}$ | \begin{aligned}x &= 6\cos \dfrac{2\pi}{3}\\&= -3\end{aligned} |
$\boldsymbol{y }$ | \begin{aligned}y &= 6\sin \dfrac{2\pi}{3}\\&= 3\sqrt{3}\end{aligned} |
$\boldsymbol{z}$ | \begin{aligned}z &= -3 \end{aligned} |
This means that $\left(6, \dfrac{2\pi}{3}, -3\right)$ is equal to $(-3, 3\sqrt{3}, -3)$ in rectangular form.
Example 3
Describe the position of the cylindrical point, $\left(2, \dfrac{\pi}{6}, 4 \right)$, then graph the point on the three-dimensional cartesian coordinate system.
Solution
To know the position of the cylindrical coordinate, convert it first to its rectangular form. That way, it’ll be easier for us to know the position of the point with respect to the three axes.
Using the same relationship shown in the previous example, we have the following:
$\boldsymbol{x}$ | \begin{aligned}x &= 2\cos \dfrac{\pi}{6}\\&= \sqrt{3}\end{aligned} |
$\boldsymbol{y }$ | \begin{aligned}y &= 2\sin \dfrac{\pi}{6}\\&= 1\end{aligned} |
$\boldsymbol{z}$ | \begin{aligned}z &= 4\end{aligned} |
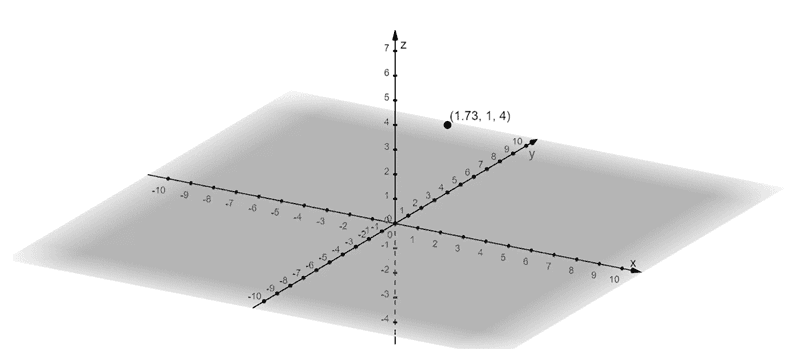
This means that the cylindrical coordinate is equivalent to $(\sqrt{3}, 1, 4)$ in rectangular form. Use this coordinate to describe the position of the point
- The point is found $\sqrt{3}$ or approximately $1.73$ units along the $x$-axis.
- We can then move the point $1$ unit away from the $x$-axis and parallel to the $y$-axis.
- Project this point along the $z$-axis so that the height of the point is $4$ units.
Use the description to graph the cylindrical coordinate in the Cartesian coordinate system.
Example 4
Describe the position of the cylindrical point, $\left(3, 120^{\circ}, 2 \right)$, then graph the point on the three-dimensional cartesian coordinate system. Include the segment connecting the point from the origin as well as $\theta$.
Solution
We’ll apply a similar process from the previous example – convert the cylindrical coordinate, $\left(4, 135^{\circ}, 2 \right)$, to its Cartesian form first as shown below.
$\boldsymbol{x}$ | \begin{aligned}x &= 3\cos 120^{\circ}\\&= -\dfrac{1}{2}\end{aligned} |
$\boldsymbol{y }$ | \begin{aligned}y &= 3\sin 120^{\circ}\\&= \dfrac{3\sqrt{3}}{2}\end{aligned} |
$\boldsymbol{z}$ | \begin{aligned}z &= 2\end{aligned} |
This means that the cylindrical coordinate, $(3, 120^{\circ}, 2)$, is equivalent to $\left(-\dfrac{1}{2}, \dfrac{3\sqrt{3}}{2}, 2\right)$. We can locate the position of the point by:
- Moving $\dfrac{1}{2}$ unit along the negative $x$-axis.
- We can then move $\dfrac{3\sqrt{3}}{2}$ or $2.60$ units away from the $x$-axis and parallel to the $y$-axis.
- Project this point along the $z$-axis so that the height of the point is $2$ units.
Use this to plot the cylindrical coordinate in the 3D coordinate system. To include $\theta$, keep in mind that the polar angle is formed by the $x$-axis and the segment connecting the point from the origin.
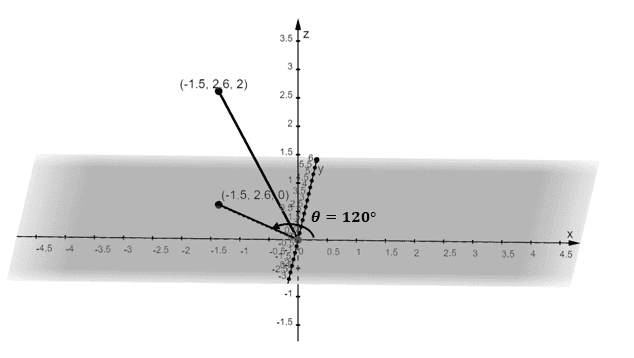
This confirms the fact that the cylindrical coordinate, $(3, 120^{\circ}, 2)$, is simply the projection of the polar coordinate, $(3, 120^{\circ})$, with respect to the $z$-axis and $2$ units above the $xy$-plane.
Practice Questions
1. Convert the following rectangular coordinates to their cylindrical forms.
a. $(1, 1, 4)$
b. $(-2, 3, 2)$
c. $(3, \sqrt{2}, -3)$
2. Convert the following cylindrical coordinates to their rectangular forms.
a. $(1, 30^{\circ}, 2)$
b. $\left(4, \dfrac{\pi}{4}, 8\right)$
c. $(2, \pi, -1)$
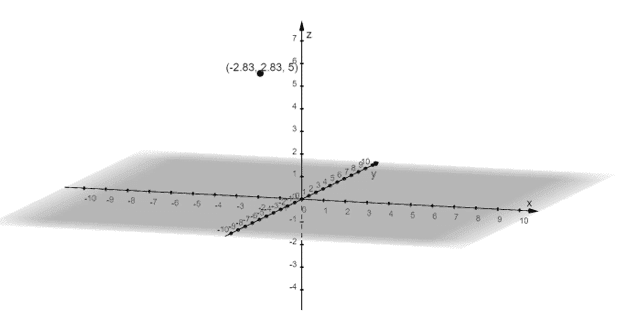
3. Describe the position of the cylindrical point, $\left(4, \dfrac{3\pi}{4}, 5 \right)$, then graph the point on the three-dimensional artesian coordinate system.
Answer Key
1.
a. $(\sqrt{2}, 45^{\circ}, 4)$ or $\left(\sqrt{2}, \dfrac{\pi}{4}, 4\right)$
b. $(\sqrt{13}, 359.02^{\circ}, 2)$
c. $(\sqrt{11}, 25.24^{\circ}, -3)$
2.
a. $\left(\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}, 2\right)$
b. $\left(2\sqrt{2}, 2\sqrt{2}, 8\right)$
c. $(-2, 0, -3)$
3.
$(-2\sqrt{2}, 2\sqrt{2}, 5)$
• The point is found $2\sqrt{2}$ or approximately $2.83$ units along the negative $x$-axis.
• We can then move $2\sqrt{2}$ or $2.83$ units away from the $x$-axis and parallel to the $y$-axis.
• Project this point along the $z$-axis so that the height of the point is $5$ units.
3D images/mathematical drawings are created with GeoGebra.
