- Home
- >
- De Moivre’s theorem – Formulas, Explanation, and Examples
JUMP TO TOPIC
De Moivre’s Theorem – Formulas, Explanation, and Examples
 De Moivre’s Theorem is an essential theorem when working with complex numbers. This theorem can help us easily find the powers and roots of complex numbers in polar form, so we must learn about De Moivre’s theorem.
De Moivre’s Theorem is an essential theorem when working with complex numbers. This theorem can help us easily find the powers and roots of complex numbers in polar form, so we must learn about De Moivre’s theorem.
De Moivre’s Theorem states that the power of a complex number in polar form is equal to raising the modulus to the same power and multiplying the argument by the same power. This theorem helps us find the power and roots of complex numbers easily.
This pattern was first observed by the French mathematician Abraham De Moivre (1667 – 1754) and was used to find the powers, roots, and even solve equations involving complex numbers.
Before we dive right into De Moivre’s theorem, make sure that we have refreshed our knowledge on complex numbers and polar forms of complex numbers.
- Make sure to review your knowledge of complex numbers and their trigonometric forms.
- It’s also important to review how we convert rectangular forms to polar forms and vice-versa.
- For the proof of De Moivre’s theorem, master your knowledge on adding, multiplying, subtracting, and dividing complex numbers as well.
In this article, we’ll learn about De Moivre’s theorem, learn how we can apply them, and appreciate this theorem for how useful it is in manipulating complex numbers.
We’ll also provide a special section for the proof of the theorem for the curious minds and those eager to learn how the theorem was established.
What is De Moivre’s Theorem?
De Moivre’s theorem helps us raise power and find the roots of complex numbers in trigonometric form. Let’s say we have $z = r (\cos \theta + i\sin \theta)$, according to De Moivre’s theorem, we can easily raise $z$ to the power of $n$.
Let’s observe how $z$ behaves when we raise it to the second and third power to check for patterns.
Starting at $z$ and $z^2$, we have the following result shown below.
$\begin{aligned}z&= r(\cos \theta + i \sin \theta )\\z^2&=r^2(\cos \theta + i\sin \theta)^2\\&= r^2(\cos^2 \theta + i2\sin \theta \cos\theta + i^2 \sin^2 \theta )\\&=r^2(\cos^2 \theta +i 2\sin \theta \cos \theta – \sin ^2 \theta)\\&= r^2(\cos^2 \theta – \sin^2 \theta + i2 \sin \theta \cos \theta\\&= r^2(\cos 2\theta + i2\sin \theta \cos \theta )\phantom{xxxxxx}\color{green} \cos 2\theta = \cos^2 \theta – \sin^2 \theta \\&= r^2(\cos 2\theta + i\sin 2\theta )\phantom{xxxxxxxxxx}\color{green} \sin 2\theta = 2\sin \theta \cos \theta \end{aligned}$
We can also use the FOIL method and the sum formulas for sine and cosine to find $z^3$.
$\begin{aligned}z^3 &= z \cdot z^2\\&r^3=(\cos \theta + i\sin \theta)(\cos 2\theta + i\sin 2\theta ) \\ &= r^3[(\cos \theta \cos 2\theta – \sin \theta \sin 2\theta)+ i(\cos \theta \sin 2\theta + \sin \theta \cos 2 \theta)] \\&=r^3[\cos(\theta + 2\theta) + i\sin( \theta +2\theta)]\\&= r^3(\cos 3\theta + i \sin 3\theta) \end{aligned}$
Have you noticed any patterns so far? Let’s list down $z$, $z^2$, and $z^3$ first, and maybe you’ll be able to spot a pattern.
$\begin{aligned}z&= r(\cos \theta + i \sin \theta)\\z^2 &=r^2 (\cos 2\theta + i\sin 2\theta)\\z^3 &= r^3(\cos 3\theta + i \sin 3\theta)\end{aligned}$
Do you have a good guess for $z^4$? Yes, $r^4 (\cos 4 \theta + i \sin 4\theta)$ is actually a good guess! You can apply a similar process from $z^3$ to find $z^4$, so try verifying the expression yourself also to help you review your knowledge of algebraic and trigonometric techniques.
Notice how tedious it will be if we want to find $z^8$? This is why De Moivre’s theorem is extremely helpful when finding complex numbers’ powers and roots.
The formula below states how we can apply the theorem to find $z^n$ easily. We can even extend this to finding the $n$th roots of $z$.
De Moivre’s theorem formula
When $n$ is a rational number and a complex number in polar or trigonometric form, we can raise the complex number by a power of $n$ using the formula shown below.
$ z^n = r^n (\cos n\theta + i\sin n\theta)$
This means that to raise $z = r (\cos \theta + i\sin \theta)$ to the power of $n$, we simply:
- Raise the modulus, $r$, by the power of $n$.
- Multiply the value of $\theta$ inside the parenthesis by $n$.

Also, we can find the roots of the complex numbers using De Moivre’s theorem.
$ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{ \theta + 2\pi k }{n}\right) $.
From the formula, we can see that we can find the $n$th root of $z$ by:
- Taking the $n$th root of the modulus, $r$.
- Divide the values of the angle by $n$.
- Repeat the process while increasing the angle by $2\pi k$, where $k = 1, 2, …n-1$.
- Make sure you have a total of $n$ complex numbers before stopping.
In the next section, you’ll see how helpful it is to know these two formulas when finding the powers, roots, and even solving equations involving the complex system.
How to use De Moivre’s Theorem?
Now that we know the two essential formulas established from De Moivre’s theorem. Let’s explore the common problems involving complex numbers that we might make use of these identities.
- We can raise any complex number (in either rectangular or polar form) to the $n$th power easily using De Moivre’s theorem. When given a complex number in rectangular form, make sure to convert it to polar form first.
- Similarly, we can find the $n$th root of complex numbers.
- We can also solve equations that involve complex number roots using De Moivre’s theorem.
| Finding the power | Find the root |
| $ z^n = r^n (\cos n\theta + i\sin n\theta)$ | $ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{ theta + 2\pi k }{n}\right) $ |
This means that if we want to find $(1 + i)^4$, we can use De Moivre’s theorem by:
- Converting $1 + i$ to polar form.
- Applying the formula $ z^n = r^n (\cos n\theta + i\sin n\theta)$.
Let’s find the modulus and argument of $1 + i$ first then write it in trigonometric form.
| $\boldsymbol{r = \sqrt{a^2 + b^2}}$ | $\boldsymbol{\theta = \tan^{-1} \dfrac{b}{a}}$ | $\boldsymbol{r(\cos \theta + i \sin \theta) }$ |
| $\begin{aligned}r &= \sqrt{1^2 + 1^2}\\&= \sqrt{2} \end{aligned}$ | $\begin{aligned}\theta &= \tan^{-1} \dfrac{1}{1} \\&= \tan^{-1} 1\\&= \dfrac{\pi}{4}\end{aligned}$ | $\sqrt{2}\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4}\right)$ |
We can now use the formula $ z^n = r^n (\cos n\theta + i\sin n\theta)$, to raise $(1 + i)^4$.
$\begin{aligned}(1 + i)^4 &= \left[\sqrt{2}\left(\cos \dfrac{\pi}{4} + i\sin \dfrac{\pi}{4}\right)\right]^4\\&=(\sqrt{2})^4 \left(\cos 4\cdot \dfrac{\pi}{4} + i\sin 4\cdot \dfrac{\pi}{4}\right )\\&=4(\cos \pi + i \sin \pi)\end{aligned}$
If we want to return an answer in rectangular, we simply evaluate $\cos \pi$ and $\sin \pi$ then distribute $4$ to each of the resulting values.
$\begin{aligned}4(\cos \pi + i \sin \pi) &= 4(-1 + 0i)\\&=-4\end{aligned}$
Hence, $(1 + i)^4$ is equal to $4(\cos \pi + i\sin \pi)$ or $-4$.
We can also find the cube root of $(1 + i) $ using the polar form of $1 + i$.
$\begin{aligned}\sqrt[3]{1 + i} &= \sqrt[3]{\sqrt{2}\left(\cos \dfrac{\pi }{4}+ i\sin \dfrac{\pi}{4}\right)} \end{aligned}$
Since we’re looking for the cube root, we’re using $k = \{0, 1, 2\}$ in the formula, $ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{ \theta + 2\pi k }{n}\right) $.
Meaning, we’re expecting three roots for our answer. It helps to keep in mind as well that we can rewrite $\sqrt[3]{\sqrt{2}}$ as a root of $6$ as shown below.
$\begin{aligned} \sqrt[3]{\sqrt{2}} & = (2^{\frac{1}{2}})^{\frac{1}{3}} \\&= 2^{\frac{1}{6}} \\&= \sqrt[6]{6}\end{aligned}$
Why don’t we start with $k = 0$?
$\begin{aligned}\sqrt[3]{\sqrt{2}\left(\cos \dfrac{\pi }{4}+ i\sin \dfrac{\pi}{4}\right)}&= \sqrt[3]{\sqrt{2}}\left( \cos \dfrac{\dfrac{\pi}{4} + 2\pi (0)}{3} + i\sin \dfrac{ \dfrac{\pi}{4} + 2\pi(0) }{3}\right) \\&=\sqrt[3]{\sqrt{2}} \left(\cos \dfrac{\pi}{12} + i\sin \dfrac{\pi}{12} \right )\\&=\sqrt[6]{2}\left(\cos \dfrac{\pi}{12} + i\sin \dfrac{\pi}{12} \right )\end{aligned}$
We’ll apply a similar when working out the two remaining roots when $k = 1$ and $k = 2$.
| $\boldsymbol{k}$ | $\boldsymbol{\sqrt[3]{1 + i}}$ |
| $k = 1$ | $\begin{aligned}\sqrt[3]{\sqrt{2}\left(\cos \dfrac{\pi }{4}+ i\sin \dfrac{\pi}{4}\right)}&= \sqrt[3]{\sqrt{2}}\left( \cos \dfrac{\dfrac{\pi}{4} + 2\pi (1)}{3} + i\sin \dfrac{ \dfrac{\pi}{4} + 2\pi(1) }{3}\right) \\&=\sqrt[3]{\sqrt{2}} \left(\cos \dfrac{3\pi}{4} + i\sin \dfrac{3\pi}{4} \right )\\&=\sqrt[6]{2}\left(\cos \dfrac{3\pi}{4} + i\sin \dfrac{3\pi}{4} \right )\end{aligned}$ |
| $k = 2$ | $\begin{aligned}\sqrt[3]{\sqrt{2}\left(\cos \dfrac{\pi }{4}+ i\sin \dfrac{\pi}{4}\right)}&= \sqrt[3]{\sqrt{2}}\left( \cos \dfrac{\dfrac{\pi}{4} + 2\pi (2)}{3} + i\sin \dfrac{ \dfrac{\pi}{4} + 2\pi(2) }{3}\right) \\&=\sqrt[3]{\sqrt{2}} \left(\cos \dfrac{17\pi}{12} + i\sin \dfrac{17\pi}{12} \right )\\&=\sqrt[6]{2}\left(\cos \dfrac{17\pi}{12} + i\sin \dfrac{17\pi}{12} \right )\end{aligned}$ |
We’ve just shown you how we can apply De Moivre’s theorem to find complex numbers’ power and roots. Don’t worry. We have more examples prepared for you!
Ever wondered how we can confirm the validity of De Moivre’s theorem? Check out the section below to understand how we can prove these formulas. This can also help you master the two formulas when you know how they were established.
If you want to jump right into trying out more problems involving De Moivre’s theorem, you can skip through the section below and start with the four examples we’ve provided.
De Moivre’s theorem proof
We can prove De Moivre’s theorem using mathematical induction. Let’s recall the process of proving a theorem using mathematical induction first.
If we want to show that $P(n)$ is true for all $n$ that is greater than or equal to, we have to:
- Show that $P(1)$ exists and is true.
- If $P(n)$ is indeed true, we have to show that $P(n + 1)$ is also true.
We’ll have to show these two conditions for De Moivre’s theorem to prove valid.
Starting with the equation, $(\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n \theta$.
For this to be true, we have to show that it is true for $n = 1$.
$ \begin{aligned}(\cos \theta + i \sin \theta)^1 &= \cos 1\theta + i\sin 1\theta\\&=\cos \theta + i\sin \theta\\&= (\cos \theta + i \sin \theta)^1\end{aligned}$
This shows that the theorem is true for $n = 1$.
Assuming that $(\cos \theta + i \sin \theta)^n = \cos n\theta + i \sin n \theta$ is indeed true, we must show that $(\cos \theta + i \sin \theta)^{n + 1} = \cos (n + 1) \theta + i \sin (n + 1) \theta$ is also true.
To do so, let’s express $(\cos \theta + i \sin \theta)^{n + 1}$ as a product of $(\cos \theta + i \sin \theta)^n$ and $\cos \theta + i \sin \theta$.
$\begin{aligned}(\cos \theta + i \sin \theta)^{n + 1} &= (\cos \theta + i\sin \theta)^n(\cos \theta + i\sin \theta)\end{aligned}$
Replace $(\cos \theta + i\sin \theta)^n(\cos \theta + i\sin \theta)^n$ with $\cos n\theta + i\sin n\theta$.
$\begin{aligned}(\cos \theta + i \sin \theta)^{n + 1} &= (\cos \theta + i\sin \theta)^n(\cos \theta + i\sin \theta)\\&= (\cos n\theta + i\sin n\theta)(\cos \theta + i \sin \theta)\end{aligned}$
Apply the FOIL method to expand the expression and replace $i^2$ with $-1$.
$\begin{aligned}(\cos \theta + i \sin \theta)^{n + 1} &=\cos n\theta \cos \theta + i \cos n\theta \sin \theta + i \sin n\theta \cos \theta + i^2 \sin n\theta \sin \theta \\&=\cos n\theta \cos \theta + i \cos n\theta \sin \theta + i \sin n\theta \cos \theta – \sin n\theta \sin \theta\\&=\cos n\theta \cos \theta – \sin n\theta \sin \theta + i \sin n \theta \cos \theta + i \cos n\theta \sin \theta\\&=(\cos n\theta \cos \theta – \sin n\theta \sin \theta )+ i (\sin n \theta \cos \theta + \cos n\theta \sin \theta) \end{aligned}$
Rewrite the grouped terms using the sum formula for cosine and sine.
$\begin{aligned}(\cos \theta + i \sin \theta)^{n + 1} &=\cos (n\theta + \theta) + i \sin (n\theta + \theta)\\&= \cos (n+1)\theta + i\sin (n + 1)\theta\end{aligned}$
We’ve just shown that $(\cos \theta + i \sin \theta)^{n + 1} = \cos (n+1)\theta + i\sin (n + 1)\theta$, meaning De Moivre’s theorem is also true for $n + 1$.
By mathematical induction, we’ve just shown that the De Moivre’s theorem, $[r(\cos \theta + i \sin \theta)]^n= r^n(\cos n\theta + i\sin n\theta)$ is also true.
Since we’ve already established De Moivre’s theorem for raising the power of complex numbers, we can also prove the formula for finding the root.
If we have $z =r ( \cos \theta + i\sin \theta)$, to take the $n$th rooth, we want to actually find $z^{\frac{1}{n}}$.
$\begin{aligned}z^{\frac{1}{n}} &= r^{\frac{1}{n}}\left( \dfrac{1}{n}\cdot \cos \theta + \dfrac{1}{n}\cdot i\sin \theta \right)\\&=r^{\frac{1}{n}}\left(\dfrac{\cos \theta}{n} + \dfrac{\sin \theta}{n} \right )\end{aligned}$
Keep in mind that the cosine and sine values will remain the same for all angles that are conterminal to $\theta$. This means that we can extend the formula to $z^{\frac{1}{n}} = r^{\frac{1}{n}}\left(\dfrac{\cos \theta + 2\pi k}{n} + \dfrac{\sin \theta + 2\pi k}{n} \right ) $, where $k = 0,1, 2,…n-1$.
Since $z^{\frac{1}{n}} = \sqrt[n]{z}$ and $r^{\frac{1}{n}} = \sqrt[n]{r}$, we can also rewrite the formula as $\sqrt[n]{z } = \sqrt[n]{r }\left(\dfrac{\cos \theta + 2\pi k}{n} + \dfrac{\sin \theta + 2\pi k}{n} \right ) $.
In degrees, we can also write this formula as $\sqrt[n]{z } = \sqrt[n]{r }\left(\dfrac{\cos \theta + 360^{\circ} k}{n} + \dfrac{\sin \theta +360^{\circ}k}{n} \right ) $.
Example 1
Find the power of the following complex numbers, then express the answer in rectangular form.
a. $\left(\cos \dfrac{2\pi}{3} + i \sin \dfrac{2\pi}{3}\right)^3$
b. $\left[2\left(\cos \dfrac{\pi}{4} + i \sin \dfrac{5\pi}{4}\right)\right]^5$
c. $(1 – \sqrt{3}i)^{12}$
Solution
For the first two items, we use the power formula from De Moivre’s theorem.
$ z^n = r^n (\cos n\theta + i\sin n\theta)$.
$ \begin{aligned}\left(\cos \dfrac{2\pi}{3} + i \sin \dfrac{2\pi}{3}\right)^3 &= (1)^3\left[\cos \left(3 \cdot\dfrac{2\pi}{3}\right) + i \sin \left(3 \cdot\dfrac{2\pi}{3}\right)\right]\\&= \cos 2\pi + i \sin 2\pi\end{aligned}$
We now have the simplified polar form to convert the complex number into a rectangular form.
$ \begin{aligned} \cos 2\pi + i \sin 2\pi &= 1 + 0i\\&=1\end{aligned}$
Hence, $\left(\cos \dfrac{2\pi}{3} + i \sin \dfrac{2\pi}{3}\right)^3$ in rectangular form is actuall equal to $1$.
Let’s go ahead and apply a similar process to simplify the second item.
$ \begin{aligned} \left[2\left(\cos \dfrac{\pi}{4} + i \sin \dfrac{5\pi}{4}\right)\right]^5 &= 2^5\left[\cos \left(5\cdot \dfrac{\pi}{4} \right ) + i \sin \left(5\cdot \dfrac{\pi}{4} \right )\right]\\&=32\left(\cos \dfrac{5\pi}{4} + i \sin \dfrac{5\pi}{4} \right )\\&=32 \left( – \dfrac{\sqrt{2}}{2} – i\dfrac{\sqrt{2}}{2}\right)\\&= 32 \cdot – \dfrac{\sqrt{2}}{2} – 32 \cdot \dfrac{\sqrt{2}}{2}\\&=-16\sqrt{2} – 16\sqrt{2}\end{aligned}$
Before we can evaluate $(1 – \sqrt{3}i)^12$, let’s convert $1 – \sqrt{3}i$ into polar form first.
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{r(\cos \theta + i\sin \theta)}$ |
| $ \begin{aligned} r&= \sqrt{(1)^2 + (\sqrt{3})^2}\\&= \sqrt{1 + 3}\\&=\sqrt{4}\\&= 2\end{aligned}$ | $ \begin{aligned} \theta &= \tan ^{-1} \dfrac{-\sqrt{3}}{1}\\&= \dfrac{5\pi}{3}\end{aligned}$ | $2 \left(\cos \dfrac{5\pi}{3} + i \sin \dfrac{5\pi}{3}\right)$ |
Let’s go ahead and raise $2 \left(\cos \dfrac{5\pi}{3} + i \sin \dfrac{5\pi}{3}\right)$ to the $12$th power.
$\begin{aligned}(1 – \sqrt{3}i)^{12}&= \left[2 \left(\cos \dfrac{5\pi}{3} + i \sin \dfrac{5\pi}{3}\right) \right ]^{12}\\&= (2^{12})\left[\cos \left(12 \cdot \dfrac{5\pi}{3} \right ) + i\sin \left(12 \cdot \dfrac{5\pi}{3} \right ) \right ]\\&= 4096 (\cos 30 \pi + i \sin 30 \pi)\\&=4096(1 + 0i)\\&= 4096\end{aligned}$
This means that $(1 – \sqrt{3}i)^{12}$, in rectangular form, is equal to $4096$.
Example 2
Find all the complex cube roots of $27$.
Solution
We can express $27$ as a complex number in rectangular form: $27 = 27 + 0i$. We can then convert $27 + 0i$ to polar form. It’s expected to lie on the positive part of the real axis (or when $\theta = 0). We can still confirm this by using the traditional approach:
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{r(\cos \theta + i\sin \theta)}$ |
| $ \begin{aligned} r&= \sqrt{(27)^2 + (0)^2}\\&= &= 2\end{aligned}$ | $ \begin{aligned} \theta &= \tan ^{-1} \dfrac{0}{27}\\&= 0 \end{aligned}$ | $27 (\cos 0 + i \sin 0)$ |
To find the three complex roots of $\sqrt[3] 27$, we use the formula for the $n$th root of $r(\cos \theta + i\sin \theta)$, $ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{ \theta + 2\pi k }{n}\right) $.
For $\sqrt[3] 27 = \sqrt[3]{27 (\cos 0 + i \sin 0)} $, we’ll use $n = 3$ and $k = \{0, 1, 2\}$.
| $\boldsymbol{k}$ | $\boldsymbol{\sqrt[3]{27 (\cos 0 + i \sin 0)} }$ |
| $k = 0$ | $\begin{aligned}\sqrt[3] {27(\cos 0+ \sin 0)} &= \sqrt[3]{27} \left(\cos \dfrac{0 + 2\pi(0)}{3} + i\sin \dfrac{0 + 2\pi (0)}{3} \right)\\&= 3 (\cos 0 + i \sin 0)\\&= 3(1 + 0)\\&= 3\end{aligned}$ |
| $k = 1$ | $\begin{aligned}\sqrt[3] {27(\cos 0 + \sin 0)} &= \sqrt[3]{27} \left(\cos \dfrac{0 + 2\pi(1)}{3} + i\sin \dfrac{0 + 2\pi(1)}{3} \right)\\&= 3 \left(\cos \dfrac{2\pi}{3}+ i \sin \dfrac{2\pi}{3} \right)\\&= 3\left(-\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right)\\&= -\dfrac{3}{2} + i\dfrac{3\sqrt{3}}{2}\end{aligned}$ |
| $k = 2$ | $\begin{aligned}\sqrt[3] {27(\cos 0 + \sin 0)} &= \sqrt[3]{27} \left(\cos \dfrac{0 + 2\pi(2)}{3} + i\sin \dfrac{0 + 2\pi(2)}{3} \right)\\&= 3 \left(\cos \dfrac{4\pi}{3}+ i \sin \dfrac{4\pi}{3} \right)\\&= 3\left(-\dfrac{1}{2} – i\dfrac{\sqrt{3}}{2}\right)\\&= -\dfrac{3}{2} – i\dfrac{3\sqrt{3}}{2}\end{aligned}$ |
In the past, we only know that the cube root of $27$ is equal to $3$, but with our knowledge of complex numbers and De Moivre’s theorem, we can find the two remaining roots!
This means that the three complex roots of $27$ are $\left\{3, -\dfrac{3}{2} + i\dfrac{3\sqrt{3}}{2}, -\dfrac{3}{2} – i\dfrac{3\sqrt{3}}{2}\right\}$.
Example 3
Plot all the complex fourth roots of $64(\cos 240^{\circ} + i\sin 240^{\circ})$ in one complex plane.
Solution
In degrees, we have the root formula from De Moivre’s theorem as $ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 360^{\circ} k}{n} + i\sin \dfrac{ \theta + 360^{\circ} k }{n}\right) $. This time, we’ll use $n = 4$ and $k = \{0, 1, 2, 3\}$.
| $\boldsymbol{k}$ | $\boldsymbol{\sqrt[4]{ 64(\cos 240^{\circ} + i\sin 240^{\circ})} }$ |
| $k = 0$ | $\begin{aligned}\sqrt[4]{ 64(\cos 240^{\circ} + i\sin 240^{\circ})} &= \sqrt[4]{64} \left(\cos \dfrac{240^{\circ} + 360^{\circ} \cdot 0}{4} + \sin \dfrac{240^{\circ} + 360^{\circ} \cdot 0}{4} \right )\\&= \sqrt[4]{64} (\cos 60^{\circ} + i\sin 60^{\circ})\\&= 4\left(\dfrac{1}{2} + i\dfrac{\sqrt{3}}{2}\right)\\&= 4 \cdot \dfrac{1}{2} + 4 \cdot i\dfrac{\sqrt{3}}{2}\\&= 2 + 2\sqrt{3}i\end{aligned}$ |
| $k = 1$ | $\begin{aligned}\sqrt[4]{ 64(\cos 240^{\circ} + i\sin 240^{\circ})} &= \sqrt[4]{64} \left(\cos \dfrac{240^{\circ} + 360^{\circ} \cdot 1}{4} + \sin \dfrac{240^{\circ} + 360^{\circ} \cdot 1}{4} \right )\\&= \sqrt[4]{64} (\cos 150^{\circ} + i\sin 150^{\circ})\\&= 4\left(-\dfrac{\sqrt{3}}{2} + i\dfrac{1}{2}\right)\\&= 4 \cdot -\dfrac{\sqrt{3}}{2} + 4 \cdot i\dfrac{1}{2}\\&= -2\sqrt{3} + 2i\end{aligned}$ |
| $k = 2$ | $\begin{aligned}\sqrt[4]{ 64(\cos 240^{\circ} + i\sin 240^{\circ})} &= \sqrt[4]{64} \left(\cos \dfrac{240^{\circ} + 360^{\circ} \cdot 2}{4} + \sin \dfrac{240^{\circ} + 360^{\circ} \cdot 2}{4} \right )\\&= \sqrt[4]{64} (\cos 240^{\circ} + i\sin 240^{\circ})\\&= 4\left(-\dfrac{1}{2} – i\dfrac{\sqrt{3}}{2}\right)\\&= 4 \cdot -\dfrac{1}{2} – 4 \cdot i\dfrac{\sqrt{3}}{2}\\&= -2 -2\sqrt{3}i\end{aligned}$ |
| $k = 3$ | $\begin{aligned}\sqrt[4]{ 64(\cos 240^{\circ} + i\sin 240^{\circ})} &= \sqrt[4]{64} \left(\cos \dfrac{240^{\circ} + 360^{\circ} \cdot 3}{4} + \sin \dfrac{240^{\circ} + 360^{\circ} \cdot 3}{4} \right )\\&= \sqrt[4]{64} (\cos 330^{\circ} + i\sin 330^{\circ})\\&= 4\left(\dfrac{\sqrt{3}}{2} – i\dfrac{1}{2}\right)\\&= 4 \cdot \dfrac{\sqrt{3}}{2} – 4 \cdot i\dfrac{1}{2}\\&= 2\sqrt{3} -2i\end{aligned}$ |
Hence, the four fourth roots of $64(\cos 240^{\circ} + i\sin 240^{\circ})$ are $\{2 + 2\sqrt{3}i , -2\sqrt{3} + 2i, -2 -2\sqrt{3}i, 2\sqrt{3} -2i \}$.
Let’s plot the four roots on one complex plane, as shown below.
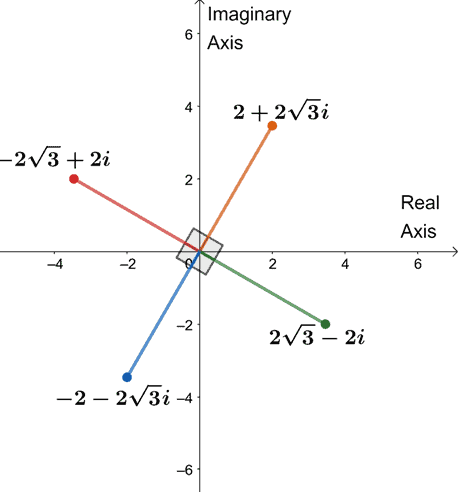
Notice something? The four roots are each $90^{\circ}$ away from each other. The segments are also all equal to $4$.
Example 4
Solve the equation $x^3 – (1 + \sqrt{3}i) = 0$ in the complex system.
Solution
First, let’s isolate $x^3$ on the left-hand side of the equation.
$ \begin{aligned}x^3 – (1 + \sqrt{3}i) &= 0\\ x^3 &= 1 + \sqrt{3}i \end{aligned}$
This means that to find the solution to a complex system equation, we need to find the cube root of $1 + \sqrt{3}i$.
For us to do this, we need to convert $1 + \sqrt{3}i$ to polar form.
| $\boldsymbol{r}$ | $\boldsymbol{\theta}$ | $\boldsymbol{r(\cos \theta + i\sin \theta)}$ |
| $ \begin{aligned} r&= \sqrt{(1)^2 + (\sqrt{3})^2}\\&= 2\end{aligned}$ | $ \begin{aligned} \theta &= \tan ^{-1} \dfrac{\sqrt{3}}{1}\\&= \dfrac{\pi}{3}\end{aligned}$ | $2 \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)$ |
Let’s find the cube root using the formula, $ \sqrt[n]{z} = \sqrt[n]{r}\left( \cos \dfrac{\theta + 2\pi k}{n} + i\sin \dfrac{ \theta + 2\pi k }{n}\right) $, where $n = 3$ and $k = \{0, 1, 2\}$.
| $\boldsymbol{k}$ | $\boldsymbol{2 \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)}$ |
| $k = 0$ | $\begin{aligned}\sqrt[3] {2 \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)} &= \sqrt[3]{2} \left(\cos \dfrac{\dfrac{\pi}{3} + 2\pi(0)}{3} + i\sin \dfrac{\dfrac{\pi}{3} + 2\pi (0)}{3} \right)\\&= \sqrt[3]{2} \left(\cos \dfrac{\pi}{9} + i \sin \dfrac{\pi}{9}\right)\end{aligned}$ |
| $k = 1$ | $\begin{aligned}\sqrt[3] {2 \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)} &= \sqrt[3]{2} \left(\cos \dfrac{\dfrac{\pi}{3} + 2\pi(1)}{3} + i\sin \dfrac{\dfrac{\pi}{3} + 2\pi (1)}{3} \right)\\&= \sqrt[3]{2} \left(\cos \dfrac{7\pi}{9} + i \sin \dfrac{7\pi}{9}\right)\end{aligned}$ |
| $k = 2$ | $\begin{aligned}\sqrt[3] {2 \left(\cos \dfrac{\pi}{3} + i \sin \dfrac{\pi}{3}\right)} &= \sqrt[3]{2} \left(\cos \dfrac{\dfrac{\pi}{3} + 2\pi(2)}{3} + i\sin \dfrac{\dfrac{\pi}{3} + 2\pi (2)}{3} \right)\\&= \sqrt[3]{2} \left(\cos \dfrac{13\pi}{9} + i \sin \dfrac{13\pi}{9}\right)\end{aligned}$ |
This means that the equation has three solutions at: $ x = \left\{\sqrt[3]{2} \left(\cos \dfrac{\pi}{9} + i \sin \dfrac{\pi}{9}\right), \sqrt[3]{2} \left(\cos \dfrac{7\pi}{9} + i \sin \dfrac{7\pi}{9}\right), \sqrt[3]{2} \left(\cos \dfrac{13\pi}{9} + i \sin \dfrac{13\pi}{9}\right)\right\}$. This actually makes sense since we expect three solutions for a cubic equation.
Practice Questions
![]()
Open Problem
Plot all the complex fourth roots of $16(\cos 240^{\circ} + i\sin 240^{\circ})$ in one complex plane.
Open Problem Solution
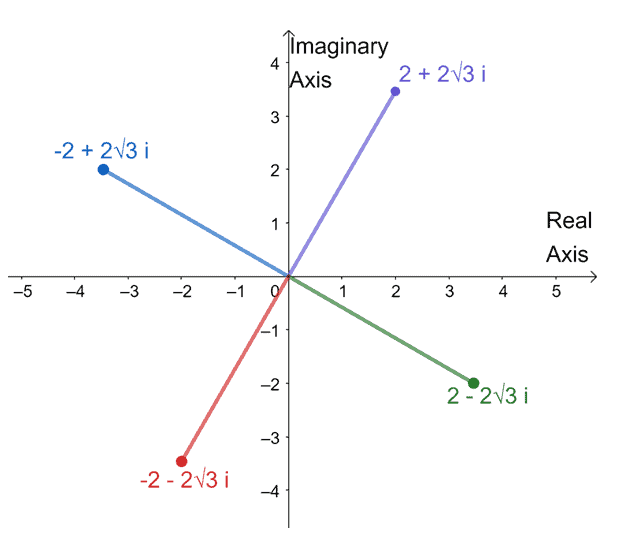
Images/mathematical drawings are created with GeoGebra.

