JUMP TO TOPIC
Dependent Events – Explanation & Examples
In probability theory, when we are dealing with multiple events, one event can change the probability of another event. For example, the probability that a randomly chosen person is suffering from some particular disease is usually small.
However, if he/she is tested positive for that disease, the probability becomes very high (the probability is still not 1 because no test is perfectly accurate). Such events are termed dependent events.
Two events are said to be dependent events if the occurrence of one event changes the probability of occurrence of the other event.
After reading this article, you should understand the following:
- Dependent events
- Identifying two events are dependent
- Solving problems related to dependent events
- Various formulae related to probabilities of dependent events
To understand the concept of dependent events, it is advisable to refresh the following topics:
What Are Dependent Events:
Suppose we roll a six-sided fair die. What is the probability of getting a $2?$ Since there are six possible outcomes and each outcome is equally likely, so the probability of getting a $2$ is $\frac16$. Now, let’s suppose we roll a die, and we know that an outcome is an even number. What is the probability that the outcome is $2?$
Now, since we know that the outcome is even, so we are left with three possible outcomes only,i.e., $\{2,4,6\}$. Since $2$ is one of the three possible equally likely outcomes, hence the probability of getting a $2$ is $\frac13$. Note that the event’s occurrence that “the outcome is even” changes the probability of $2$ from $\frac16$ to $\frac13$. Hence, the outcome is $2$, and the event that the outcome is even are dependent events.
Note that dependence works both ways. The probability of getting an even number is $\frac{3}{6} = \frac12$. However, if we know that the outcome is $2$, then the probability that the “outcome is even” becomes $1$ (since now we know that the outcome is $2$, which is an even number).
Note that again we observe that one event (in this case $2$) has changed the probability of another event (in this case, even numbers).
How to Tell If Two Events Are Dependent
To analyze whether two events are dependent or not, we first need to understand the concept of conditional probability.
Conditional Probability
Conditional probability $P(A|B)$ is the probability of event A given the information that B has already taken place. For any two events $A$ and $B,$ $P(A|B)$ is given as
$P(A|B) = \frac{P(A \cap B)}{P(B)}$
Let’s reconsider an example
Example 1:
We roll a six-sided fair die. Let $E1$ be the event that the outcome is $3$. Let $E2$ be the event that the outcome is odd. Find $P(E1|E2)$.
Solution:
Note that the sample space(link) $S = \{1,2,3,4,5,6\}$ has six elements. Also, $E1=\{3\}$ and $E2 = \{1,3,5\}$ and $E1 \cap E2 = \{3\}$, hence $P(E2) = \frac36$ and $P(E1 \cap E2) = \frac16$. Therefore,
$P(E1|E2) = \frac{\frac16}{\frac36} = \frac13$.
Conditional Probability and dependence
Now that we have the tool of conditional probability with us, we can easily define the concept of dependence mathematically. By definition, $A$ and $B$ are dependent if the occurrence of $B$ changes the probability of $A$, and similarly, the occurrence of $A$ affects the probability of $B$. Using the concept of conditional probability, we can write that $A$ AND $B$ are dependent if $P(A|B) \neq P(A)$ and $P(B|A) \neq P(B)$. The formula of conditional probability states that $P(A|B) = \frac{P(A \cap B)}{P(B)}$. Hence, if $P(A|B) \neq P(A)$, then
$P(A \cap B) = P(A|B)P(B) \neq P(A)P(B)$
Similarly, we can show that if $P(A \cap B) \neq P(A)P(B)$, then
$P(B|A) \neq P(B)$
Dependent Events Definition
Two events are said to be dependent if the occurrence of one event changes the probability of occurrence of the other event.
Mathematically, two events $A$ and $B$ are said to be independent if $P(A \cap B) \neq P(A)P(B)$.
How to Solve Dependent Events
Let us consider an example to see how to solve dependent events using the above definition.
Example 2:
We toss a coin three times. Let $E1$ is the event that the first toss results in Heads. Let $E2$ is the event, the third toss is Tails, and let $E3$ is when we get an even number of tails.
- Are $E1$ and $E2$ dependent events?
- Are $E2$ and $E3$ dependent events?
- Are $E3$ and $E1$ dependent events?
Solution:
The sample space of the experiment can be written as follows:
$S = \{HHH, HHT, HTH, THH, TTT, TTH, THT, HTT\}$.
The event $E1$ can be written as
$E1 = \{HHH, HHT, HTH, HTT\}$,
$E2$ can be written as
$E2 = \{HHT, TTT, THT, HTT\}$
and $E3$ is written as
$E3 = \{TTH, THT, HTT\}$
There are $8$ elements in the sample space and $4$ elements in $E1$, $4$ in $E2$ and $3$ in $E3$. Since all elements are equally likely, hence
$P(E1) = \frac48 = \frac12$
$P(E2) = \frac48 = \frac12$
$P(E1) = \frac38$
1)
To find if $E1$ and $E2$ are dependent or not, we need to find $P(E1 \cap E2)$. Note that $E1 \cap E2 = \{HTT, HHT\}$, hence $P(E1 \cap E2) = \frac28 = \frac14$.
Now $P(E1) \times P(E2) = \frac12 \times \frac12 = \frac14 = P(E1 \cap E2)$, hence $E1$ and $E2$ are NOT dependent events.
2)
We note that $E2 \cap E3 = \{THT, HTT\} = \frac28 = \frac14$. Now,
$P(E2) \times P(E3) = \frac12 \times \frac38 = \frac{3}{16} \neq P(E1 \cap E2)$, hence $E2$ and $E3$ are dependent events.
3)
We find $E1 \cap E3 = \{HTT\}$, hence $P(E1 \cap E3) = \frac18$. Also,
$P(E1) \times P(E3) = \frac12 \times \frac38 = \frac{3}{16} \neq P(E1 \cap E3)$, hence $E1$ and $E3$ are dependent events.
Dependent Events Formula
We list the various relations between $A$ and $B$, if $A$ and $B$ are dependent
1. $P(A|B)$ = $\frac{P(A\cap B)}{P(B)} \neq P(A)$
2. $P(B|A) = \frac{P(A \cap B)}{P(A)} \neq P(B)$
3. $P(A \cap B) = P(A|B)P(B) = P(B|A)P(A) \neq P(A)P(B)$
5. $P(A \cup B) = P(A) + P(B) – P(A \cap B)$
Example 3:
The probability that a test for a certain disease comes out positive given that the patient actually has the disease is $95\%$. The probability that a randomly chosen person is infected is $1\%$. The probability that a randomly chosen person is tested positive is $10.85\%$. A person is tested positive, what is the probability that he/she actually has the disease.
Solution:
Let $P(D)$ is the probability of disease and is equal to $0.01$. $P(T)$ is the probability that the test is positive and is given to be $0.1085$. Let $P(T/D)$ is the probability that the test is positive given that the person actually has the disease and is known to be $0.95$. We are interested in the probability of disease given that the test is positive, i.e., $P(D/T)$.
From the formula listed for dependent events, we note that
$P(D/T) = \frac{P(D \cap T)}{P(T)}$,
we know $P(T)$ but we do not know $P(D \cap T)$. To find $P(D \cap T)$, we use the relation that
$P(T/D) = \frac{P(D \cap T)}{P(D)}$, hence
$P(D \cap T) = P(T/D)P(D) = 0.95 \times 0.01 = 0.0095$.
Now,
$P(D/T) = \frac{P(D \cap T)}{P(T)} = \frac{0.0095}{0.1085} = 0.087 = 8.7\%$.
Dependent Events and Tree Diagrams:
There are many scenarios of interest where we repeat the same experiments many times. For instance, tossing a coin or picking a card from a deck, etc. Tree diagrams offer a useful tool to analyze such events. Let us consider how to make tree diagrams when we know that the multiple attempts or trials of the same experiment are dependent.
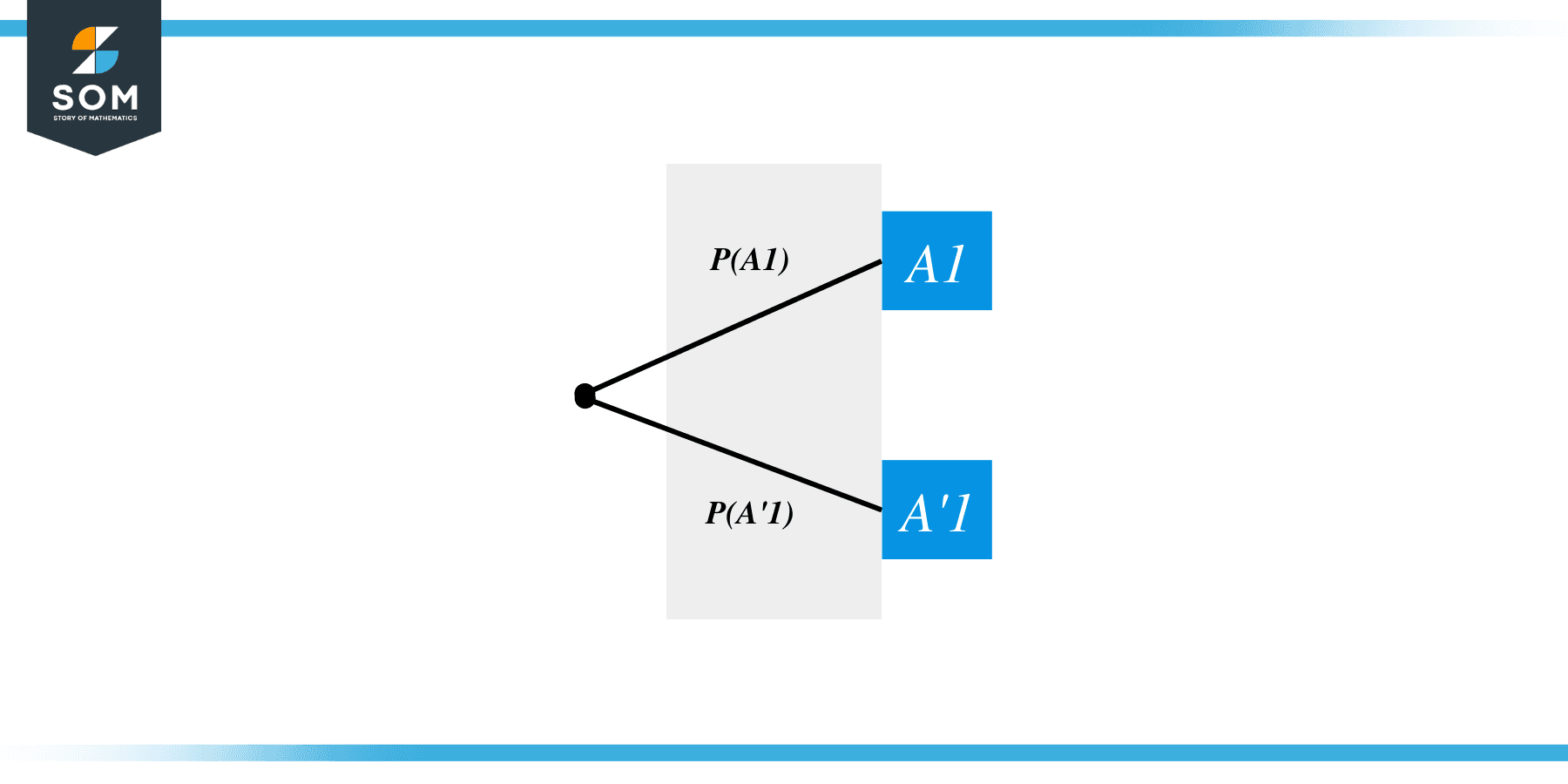
For simplicity, we consider an experiment with two outcomes only. Let’s call those $A$ and $A’$. When the experiment is performed the first time, we can have two possible outcomes, as shown in the tree diagram below. Therefore, we label the branches of the tree diagram with the probabilities of the events $A1$ and $A’1$, where $1$ denotes that the first attempt.
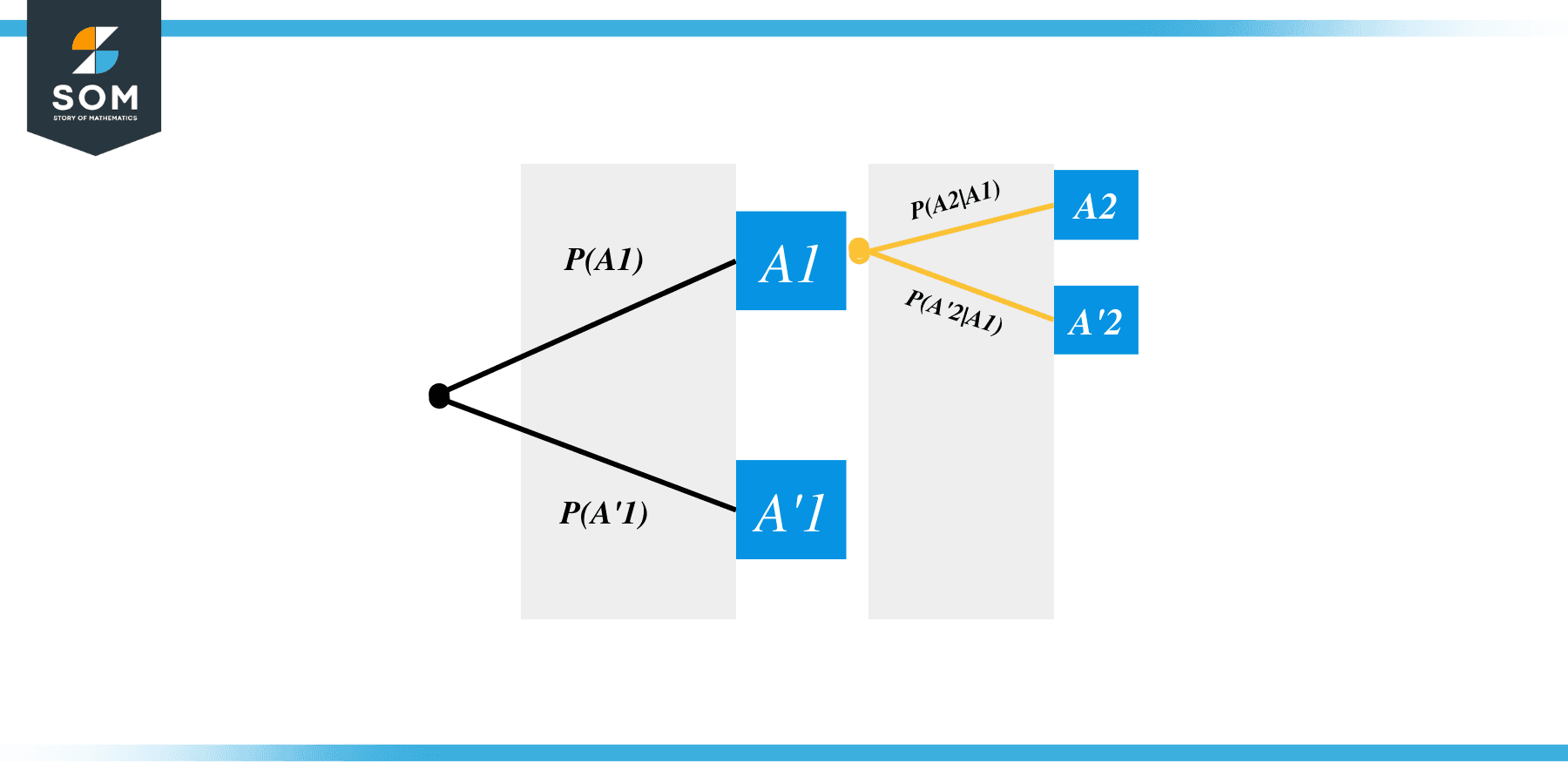
Now we perform the same experiment again. If the outcome of the first attempt was $A$, then we get a tree diagram as shown below. Note that, in this case, we are drawing the branches of the tree diagram for the case when the first outcome is known to be $A$. Hence the branches are labeled with probabilities $P(A2|A1)$ and $P(A’2|A1)$.
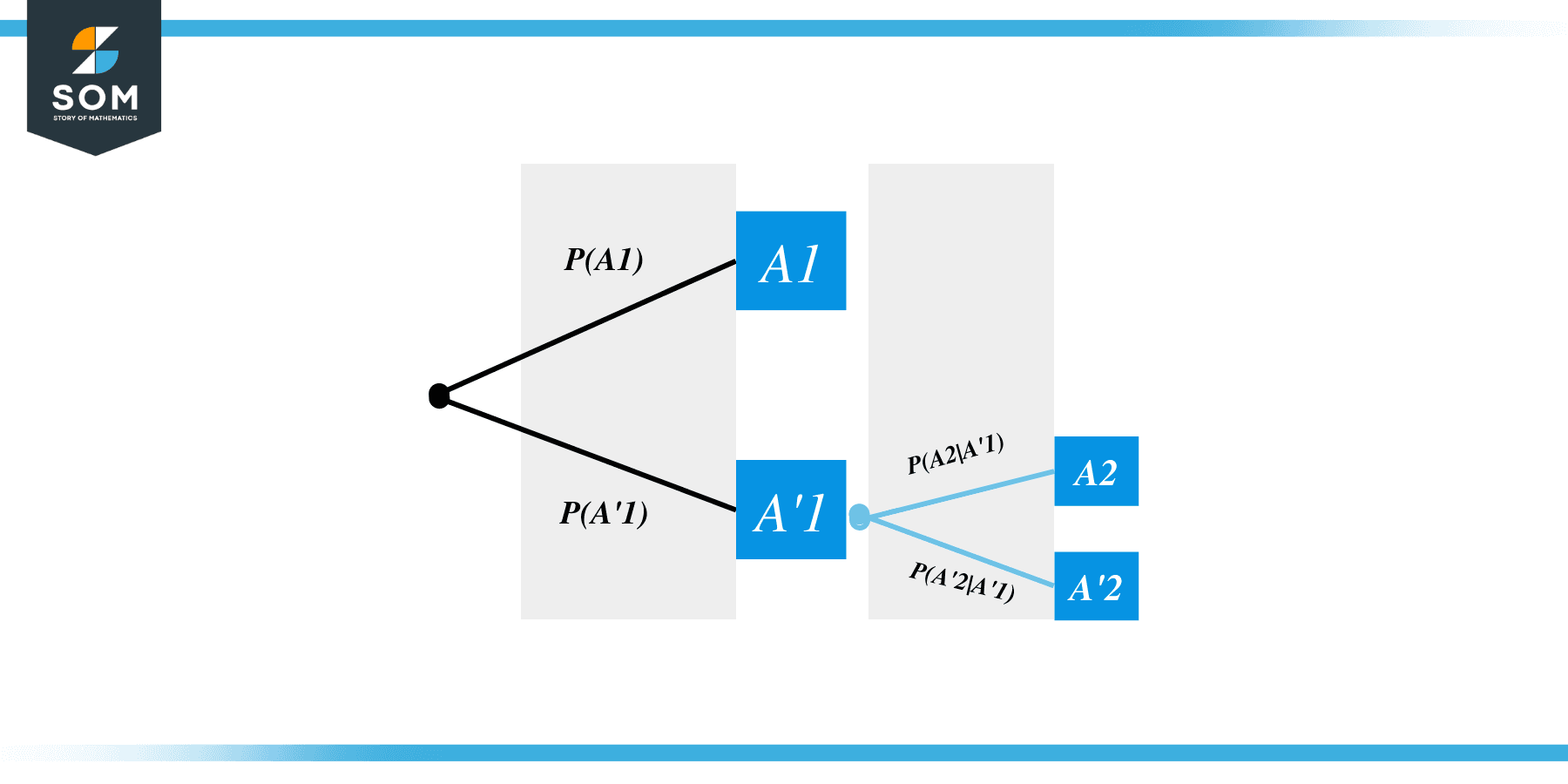
Similarly, we draw the branches when the first attempt was $A’$, as shown below.
The overall tree diagram is as follows.
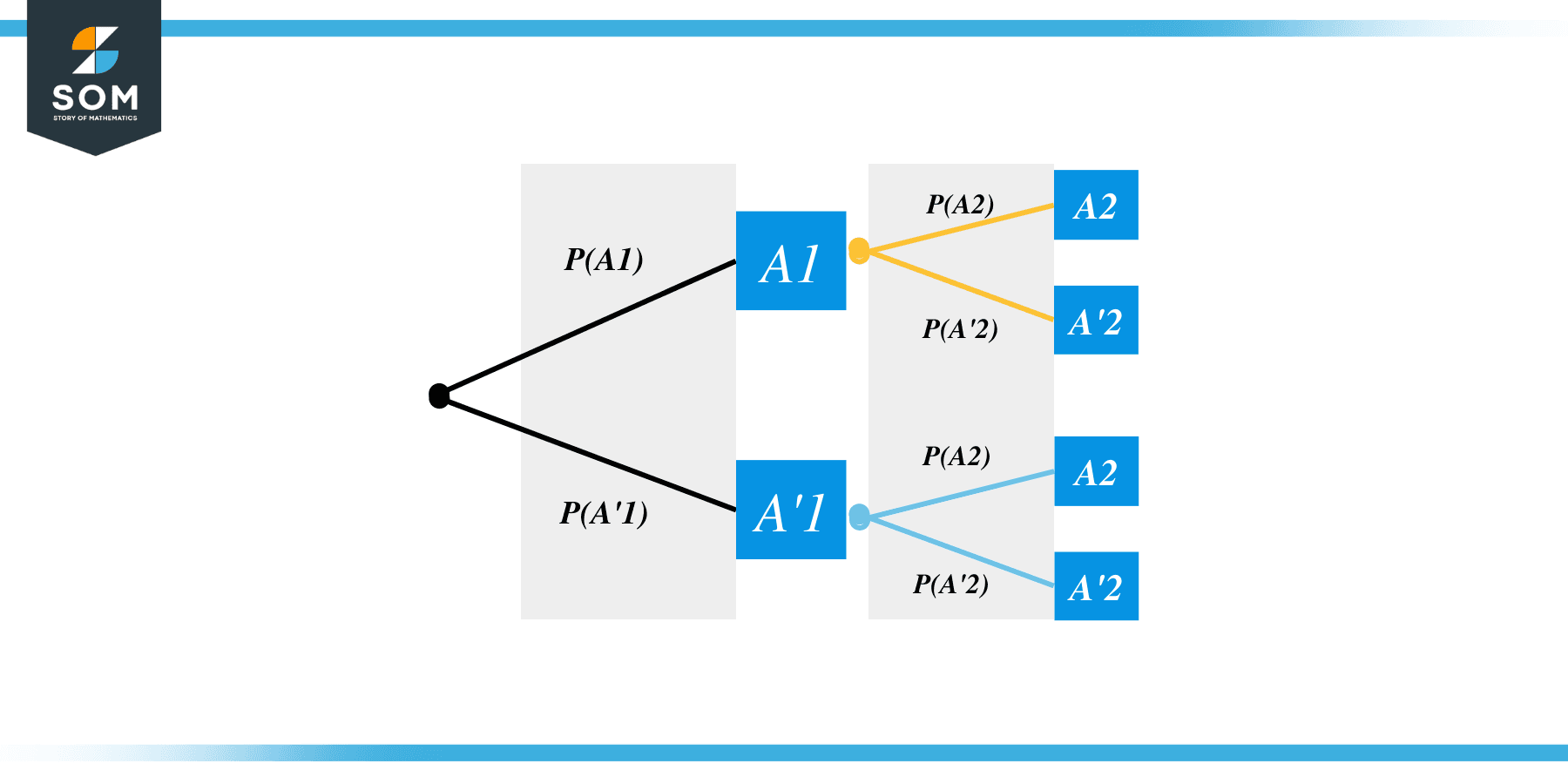
Note that the tree diagrams’ leaves (i.e., endpoints or terminal nodes) represent mutually exclusive events. Let’s say we wish to find the probability of the event $A1A2 = A1 \cap A2$, i.e., the first attempt resulted in $A$ and the second attempt also resulted in $A$. We use the fact that $P(A1 \cap A2) = P(A1)\times P(A2|A1)$. In other words, to find the probability of any event given by the terminal node of the tree diagram, we multiply the probabilities along the branches. Also, if we are interested in the probability of the compound event, say $A1A2 \cup A1A’2$, then we add the probabilities $P(A1A2)$ and $P(A1A’2)$ as the events are mutually exclusive.
Example 4:
We have two boxes, $B1$ and $B2$. $B1$ contains two red balls and three green balls. $B2$ contains three green and three red balls. We toss a coin, and if the outcome is Heads, we sample a ball from $B1$; otherwise, we sample a ball from $B2$. Draw a tree diagram and find the probability of sampling a red ball.
Solution:
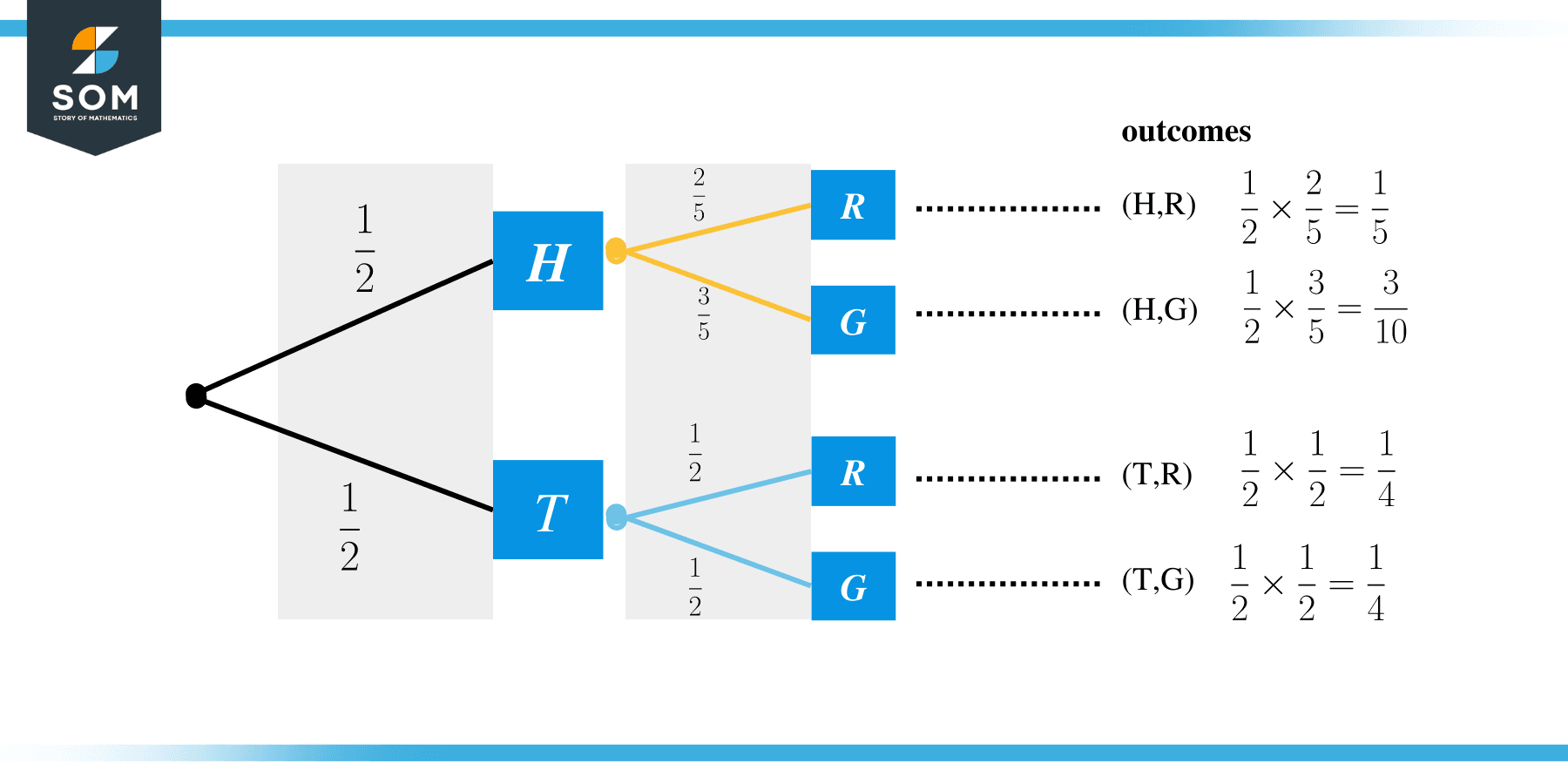
Hence the probability of drawing a Red ball is $\frac25\times \frac12 + \frac12 \times \frac12 = \frac15 + \frac14 = \frac{9}{20}$.
Sampling Without Replacement and Dependent Events:
In sampling experiments, we collect $n$ objects, and we sample from the collection $k$ times. There are two possible ways of sampling
- We replace the sampled object in the collection.
- We do not replace the sample object in the collection (i.e., sampling without replacement).
When we are doing sampling without replacement, the outcomes of each sample affect the probabilities of other samples. Hence the trials in sampling without replacement are dependent. Let us consider an example:
Example 5:
We sample two cards from a deck of 52 cards without replacement. What is the probability that the first card is a King and the second card is a Queen.
Solution:
There are $4$ kings in a deck of 52 cards. So the probability of drawing a king in the first attempt is given as
$P(\textrm{First card is a King}) = \frac{4}{52} = \frac{1}{13}$.
There are $4$ Queens in a deck. If we have already drawn a king in the first attempt, so we are left with $51$ cards. Hence, drawing a Queen in the second attempt given that the first attempt was as King is given as
$P(\textrm{Second card is a Queen}) | \textrm{First Card is a King}) = \frac{4}{51}$.
Using the formulae described above, we can write
$P(\textrm{First King AND Second Queen}) = P(\textrm{First King} \cap \textrm{Second Queen})$
$P(\textrm{First King} \cap \textrm{Second Queen}) = P(\textrm{Second Queen | First King)}P(\textrm{First King})$
$P(\textrm{First King} \cap \textrm{Second Queen})= \frac{4}{51} \times \frac{1}{13} = 0.006 = 0.6\%$
Practice Questions:
1.We roll a fair die twice. Let $E1$ be the event that the sum is even, and let $E2$ be the event that the sum is greater than $5$. Are $E1$ and $E2$ dependent?
2.The probability that Team-A wins a match is $P(W) = 65\%$. However, if Team-A is playing the match in their home ground, then the probability of winning increases to $P(W|\textrm{Home}) = 70\%$. Team-A plays equal matches in “Home ground” and “Away ground,” so the probability of playing at home is $P(\textrm{Home}) = 50\%$. If it is known that Team-A has won a match, what is the probability that the match was being played at home ground, i.e., $P(\textrm{Home}|W)$?
3.A box contains $100$ items. There are $4$ items that are defective. We sample two items from the box without replacement. Draw a tree diagram and find the probability of at most one defective item.
4.We sample two cards from a deck of $52$ cards without replacement. What is the probability that
a) Both are Kings
b) We get at least one King
Answer Key
1.Yes, $P(E1) = \frac12$, $P(E2) = \frac{13}{18}$, $P(E1 \cap E2) = \frac{7}{18} \neq P(E1) \times P(E2)$. Hence, the events are dependent.
2. $53.8$
3.
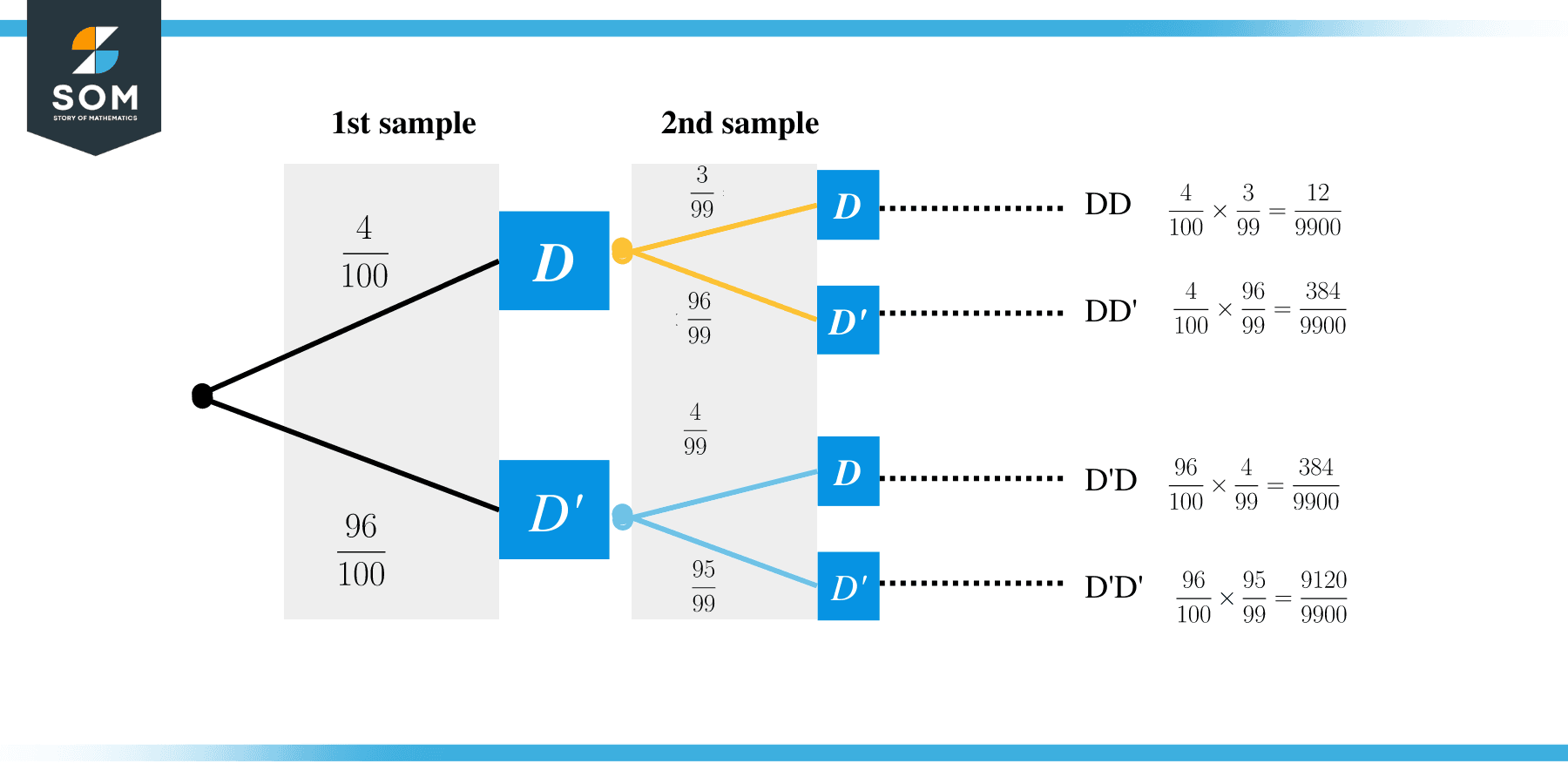
$\frac{4}{100}\frac{96}{99} + \frac{96}{100}\frac{4}{99} + \frac{96}{100}\frac{95}{99}$.
4.
a) $\frac{1}{13} \times \frac{3}{51}$.
b) $1 – (\frac{48}{52}\times\frac{47}{51})$.