- Home
- >
- Derivative of arctan – Derivation, Explanation, and Example
Derivative of arctan – Derivation, Explanation, and Example
In this article, we’ll focus on understanding the process of determining the derivative of arctan and use it to simplify the derivative of other functions. Knowing how to find the inverse tangent’s derivative expression will also help us integrate expressions once we’re taking integral calculus lessons.
The derivative of arctan returns an algebraic expression. We can use this expression to find the derivative of inverse trigonometric functions.
In our discussion, we’ll understand how to differentiate arctan and use the new derivative rule to differentiate more complex functions. Make sure to have your notes handy!
What is the derivative of arctan?
The derivative of arctan or $y = \tan^{-1}x$ can be determined using the formula shown below.
\begin{aligned}\tan y = x &\Leftrightarrow y = \tan^{-1} x\\\dfrac{d}{dx} \tan^{-1} x &= \dfrac{1}{1 + x^2} \end{aligned}
Recall that the inverse tangent of $x$ is simply the value of the angle, $y$ in radians, where $\tan y = x$. This shows that the derivative of the inverse tangent function is indeed an algebraic expression. This means that if $f(x) = \tan^{-1} x$, $f’(a)$ is simply equal to the reciprocal of $1 + a^2$.
For example, if we want to find $f’\left(\dfrac{1}{\sqrt{3}}\right)$, we can simply substitute $x = \dfrac{1}{\sqrt{3}}$ into the formula for the derivative of arctan, $f’(x) = \dfrac{1}{1 + x^2}$.
\begin{aligned}f(x)&= \tan^{-x}\\f'(x)&= \dfrac{1}{1 +x^2}\\\\f’\left({\color{Teal}\dfrac{1}{\sqrt{3}}} \right )&= \dfrac{1}{1 +\left({\color{Teal}\dfrac{1}{\sqrt{3}}} \right )^2}\\&= \dfrac{1}{1 + \dfrac{1}{3}} \\&= \dfrac{3}{4}\end{aligned}
We can also use the derivative rule for arctan to differentiate functions that contain tangent inverse (or arctan) in its expression. Before we do so, let’s take a quick look on how we were able to come up with the derivative rule, $\dfrac{d}{dx} \tan^{-1} x = \dfrac{1}{1+x^2}$.
How to derive arctan within a function?
As we have mentioned, when $y = \tan^{-1} x$, this means that $\tan y = x$. We can then take the derivative of both sides of the new equation. Keep in mind that we’ll have to use the chain rule for $\tan y$ as shown below.
Derivative of arctan proof
\begin{aligned}y&= \tan^{-1}x\\\tan y &= x\\\dfrac{d}{dx}\tan y &= \dfrac{d}{dx}x\\ {\color{Teal}\sec^2 y} \cdot {\color{Purple}\dfrac{dy}{dx}} &= \dfrac{d}{dx}x,\phantom{x}{\color{Teal}\text{Derivative of Tangent }}\text{&}{\color{Purple}\text{ Chain Rule }}\\\dfrac{d}{dx}\tan y &= \dfrac{d}{dx}x\\ {\sec^2 y} \cdot {\dfrac{dy}{dx}} &= {\color{Teal}1},\phantom{x}{\color{Teal}\text{Power Rule }}\end{aligned}
We can divide both sides by $\sec^2 y$ and rewrite $\dfrac{1}{\cos^ y}$ as $\sec^2 y$.
\begin{aligned} {\sec^2 y} \cdot {\dfrac{dy}{dx}} &= 1\\\dfrac{dy}{dx} &= \dfrac{1}{\sec^2 y}\\\dfrac{dy}{dx} &= \cos^2 y\\y’ &= \cos^2 y\end{aligned}
Remember that $y = \tan^{-1} x$, so we can use this expression to rewrite $y’$.
\begin{aligned} y’ &= \cos^2 ( \tan^{-1} x)\end{aligned}
We can use the right triangle shown below to show the fact that $\cos^2 (\tan^{-1} x)$ is indeed equal to $\dfrac{1}{1 + x^2}$.
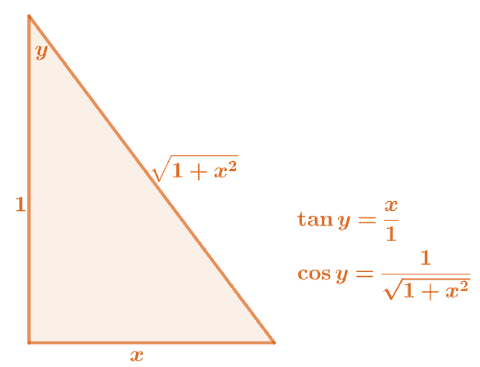
By visually representing $\tan y = x$ and $y =\tan^{-1} x$ on a right triangle and using the Pythagorean theorem, $c^2 =a^2 +b^2$, we can come up with the following.
\begin{aligned}\cos y &= \dfrac{1}{\sqrt{1 +x^2}}\\ \cos^2 y &= \dfrac{1}{1 + x^2}\end{aligned}
We can substitute this expression into our current expression for $y’$ as shown below.
\begin{aligned} y’ &= \cos^2 ( \tan^{-1} x)\\&= \dfrac{1}{1 + x^2}\end{aligned}
This confirms our derivative rule, $\dfrac{d}{dx} \tan^{-1} x = \dfrac{1}{1 + x^2}$.
Now that we’ve proven the derivative of arctan, it’s time that we use this to differentiate functions that contain $\tan^{-1}x$ within its terms or contain $\tan^{-1} g(x)$. When you’re ready, try out the examples we’ve prepared for you.
Example 1
Find the derivative of $h(x) = \tan^{-1} \sqrt{x}$.
Solution
As with differentiating other inverse trigonometric functions, it’s helpful to remember that the chain rule will apply if we have another function (other than $x$, of course) inside $\tan^{-1} x$. We can rewrite $h(x)$ as $f[g(x)]$, where $f(x)$ is the outer function and $g(x)$ is the inner function.
\begin{aligned}h’(x) &= \dfrac{d}{dx} f[g(x)] \\&= f'[g(x)] \cdot g'(x)\\f(x) &= \tan^{-1} x\\ g(x) &= \sqrt{x}\\f[g(x)] &= \tan^{-1} (\sqrt{x})\end{aligned}
We can now use the formula for the derivative of arctan, $\dfrac{d}{dx}\tan^{-1}x =\dfrac{1}{1+x^2}$.
\begin{aligned}h'(x)&= {\color{Teal}\dfrac{1}{1 + [g(x)]^2}} \cdot g'(x),\phantom{x} {\color{Teal} \text{Derivative of Tangent Inverse}}\\&= \dfrac{1}{1 + (\sqrt{x})^2} \cdot \dfrac{d}{dx} \sqrt{x}\\&= \dfrac{1}{1 + (\sqrt{x})^2} \cdot \dfrac{d}{dx} x^{\frac{1}{2}}\\&= \dfrac{1}{1 + x} \cdot {\color{Teal}\dfrac{1}{2}x^{\frac{1}{2} -1}},\phantom{x} {\color{Teal} \text{Power Rule}}\\&= \dfrac{1}{2(1 + x)}\cdot x^{-\frac{1}{2}}\\&= \dfrac{1}{2\sqrt{x}(1 + x)}\end{aligned}
This shows that it is important for us to master our fundamental derivative rules even when we’re finding the derivatives of inverse trigonometric functions or functions that contain $\tan^{-1} x$. Hence, we have $h’(x) = \dfrac{1}{2\sqrt{x}(1 + x)}$.
Example 2
Find the derivative of $h(x) = \tan^{-1} [e^x(x^3 + 3x)]$.
Solution
We will be using the chain rule to differentiate $h(x)$, so we will need the derivative of $e^x(x^3 + 3x)$. We can do this first by using the product rule, $\dfrac{d}{dx} [f(x)g(x)] = f’(x) g(x) + g’(x)f(x)$, where $f(x)= e^x$ and $g(x) = x^3 + 3x$ for our case.
\begin{aligned}\dfrac{d}{dx}[e^x(x^3 + 3x)] &= e^x \dfrac{d}{dx}(x^3 + 3x) + (x^3 + 3x)\dfrac{d}{dx} e^x \\&= e^x \dfrac{d}{dx}(x^3 + 3x) + (x^3 + 3x){\color{Teal} e^x},\phantom{x}{\color{Teal}\text{Derivative of }e^x} \\&= e^x {\color{Teal}\left(\dfrac{d}{dx} x^3 + \dfrac{d}{dx}3x\right)} + (x^3 + 3x)e^x,\phantom{x}{\color{Teal}\text{Sum Rule}}\\&= e^x (\dfrac{d}{dx} x^3+ {\color{Teal}3\dfrac{d}{dx} x })+ (x^3 + 3x)e^x,\phantom{x}{\color{Teal}\text{Constant Multiple Rule}}\\&= e^x ({\color{Teal}3x^2 + 3 })+ (x^3 + 3x)e^x,\phantom{x}{\color{Teal}\text{Power Rule}}\\&= e^x(x^3+3x^2+3x+3) \end{aligned}
Let’s now focus on our actual function, $h(x) = \tan^{-1} [e^x(x^3 + 3x)]$, and apply the chain rule as shown below.
\begin{aligned}h’(x) &= \dfrac{d}{dx} f[g(x)] \\&= f'[g(x)] \cdot g'(x)\\f(x) &= \tan^{-1} x\\ g(x) &= e^x(x^3 + 3x)\\f[g(x)] &= \tan^{-1}[e^x(x^3 + 3x)]\end{aligned}
\begin{aligned}h'(x)&= {\color{Teal}\dfrac{1}{1 + [g(x)]^2}} \cdot g'(x),\phantom{x} {\color{Teal} \text{Derivative of Tangent Inverse}}\\&= \dfrac{1}{1 + [e^x(x^3 + 3x)]^2} \cdot \dfrac{d}{dx} [e^x(x^3 + 3x)]\\&= \dfrac{1}{1 + e^{2x}(x^3 + 3x)^2} \cdot \dfrac{d}{dx} [e^x(x^3 + 3x)]\end{aligned}
What we can do now is replace $\dfrac{d}{dx} [e^x(x^3 + 3x)]$ with its derivative, $e^x(x^3+3x^2+3x+3)$.
\begin{aligned}h'(x)&= \dfrac{1}{1 + e^{2x}(x^3 + 3x)^2} \cdot {\color{Teal}e^x(x^3 + 3x^2 + 3x + 3)}, \phantom{x}{\color{Teal} \text{Product Rule}}\\&= \dfrac{e^x(x^3 + 3x^2 + 3x + 3)}{1 + e^{2x}(x^3 + 3x)^2}\end{aligned}
Hence, through fundamental derivative rules and the derivative of arctan, we have $h’(x) = \dfrac{e^x(x^3 + 3x^2 + 3x + 3)}{1 + e^{2x}(x^3 + 3x)^2}$.
Practice Questions
1. Find the derivative of the following functions.
a. $f(x) = \tan^{-1} (2x^2 -1)$
b. $g(x) = \tan^{-1} \sqrt[3]{x}$
c. $h(x) = \tan^{-1} \left(\dfrac{1}{2x + 1}\right)$
2. Find the derivative of the following functions.
a. $f(x) = \tan^{-1} \sqrt{4x^2 + 5}$
b. $g(x) = \tan^{-1} \left(\dfrac{\ln x}{4x – 1}\right)$
c. $h(x) = \tan^{-1} [e^x(x^4 – 4x)]$
Answer Key
1.
a. $f’(x) = \dfrac{2x}{2x^4-2x^2+1}$
b. $g’(x) =\dfrac{1}{3x^{\frac{2}{3}}\left(x^{\frac{2}{3}}+1\right)}$
c. $h’(x) =-\dfrac{1}{2x^2+2x+1}$
2.
a. $f’(x) = \dfrac{2x}{(2x^2 +3)\sqrt{4x^2 + 5}}$
b. $g’(x) =\dfrac{4x-1-4x\ln \left(x\right)}{x \left(\ln ^2\left(x\right) + \left(4x- 1\right)^2\right)}$
c. $h’(x) =\dfrac{e^x\left(x^4 – 4x\right) + e^x\left(4x^3 – 4\right)}{e^{2x}\left(x^4 – 4x\right)^2 +1}$
Images/mathematical drawings are created with GeoGebra.
