Determinant of a Matrix – Explanation & Examples

The determinant of a matrix is a scalar value of immense importance. With the help of the determinant of matrices, we can find useful information of linear systems, solve linear systems, find the inverse of a matrix, and use it in calculus. Let’s take a look at the definition of the determinant:The determinant of a matrix is a scalar value that results from certain operations with the elements of the matrix.In this lesson, we will look at the determinant, how to find the determinant, the formula for the determinant of $ 2 \times 2 $ and $ 3 \times 3 $ matrices, and examples to clarify our understanding of determinants. Let us start!

What is the Determinant of a Matrix?

The determinant of a matrix is a single constant value (or, a scalar value) that tells us certain things about the matrix. The value of the determinant results from certain operations that we do with the elements of a matrix.There are $ 3 $ ways we use to denote the determinant of a matrix. Check the picture below:

On the left-hand side is Matrix $ A $. This is how we write a matrix.On the right-hand side are $ 3 $ notations for determinants of matrices. We can denote the determinant of Matrix $ A $ by writing $ det( A ) $, $ | A | $, or by putting all the elements of the matrix inside two vertical bars (as shown). All these $ 3 $ notations denote the determinant of a matrix.

How to Find the Determinant of a Matrix

So how do we find the determinant of matrices?First of all, we can only calculate the determinant for square matrices!There aren’t any determinant for non-square matrices.Now, there is a formula (algorithm) to find the determinant of any square matrix. That is out of the scope of this lesson. Rather, we will look at finding determinants of $ 2 \times 2 $ matrices and $ 3 \times 3 $ matrices. The formula can be extended to find the determinant of $ 4 \times 4 $ matrices, but that is too complicated and messy!Below, we look at the formula for $ 2 \times 2 $ matrices and $ 3 \times 3 $ matrices and see how to calculate the determinant of such matrices.

Matrix Determinant Formula

We will find the determinant of $ 2 \times 2 $ and $ 3 \times 3 $ matrices in this section.

Determinant of a 2 x 2 Matrix

Consider the $ 2 \times 2 $ matrix shown below:$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} $The formula for the determinant of a $ 2 \times 2 $ matrix is shown below:$ det( A ) = | A | = \begin{vmatrix} { a } & { b } \\ { c } & { d } \end {vmatrix} = ad – bc $Note: We used $ 3 $ different notations to denote the determinant of this matrixTo find the determinant of a $ 2 \times 2 $ matrix, we take the product of the top-left entry and the bottom-right entry and subtract from it the product of top-right entry and the bottom-left entry.Let’s calculate the determinant of matrix $ B $ shown below:$ B = \begin{bmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {bmatrix} $Using the formula just learned, we can find the determinant:$ det( B ) = | B | = \begin{vmatrix} { 1 } & { 3 } \\ { – 3 } & { 2 } \end {vmatrix} $$ = ( 1 ) ( 2 ) – ( 3 ) ( – 3 ) $$ = 2 + 9 $$ = 11 $The determinant of matrix $ B $ is calculated to be $ 11 $.

Determinant of a 3 x 3 Matrix

Now that we have learned how to find the determinant of a $ 2 \times 2 $ matrix, it will become handy when finding the determinant of a $ 3 \times 3 $ matrix. Consider Matrix $ B $ shown below:$ B = \begin{bmatrix} { a } & { b } & { c } \\ { d } & { e } & { f } \\ { g } & { h } & { i } \end {bmatrix} $The formula for the determinant of a $ 3 \times 3 $ matrix is shown below:$ det( B ) = | B | = a \begin{vmatrix} { e } & { f } \\ { h } & { i } \end{vmatrix} – b \begin{vmatrix} { d } & { f } \\ { g } & { i } \end{vmatrix} + c \begin{vmatrix} { d } & { e } \\ { g } & { h } \end{vmatrix} $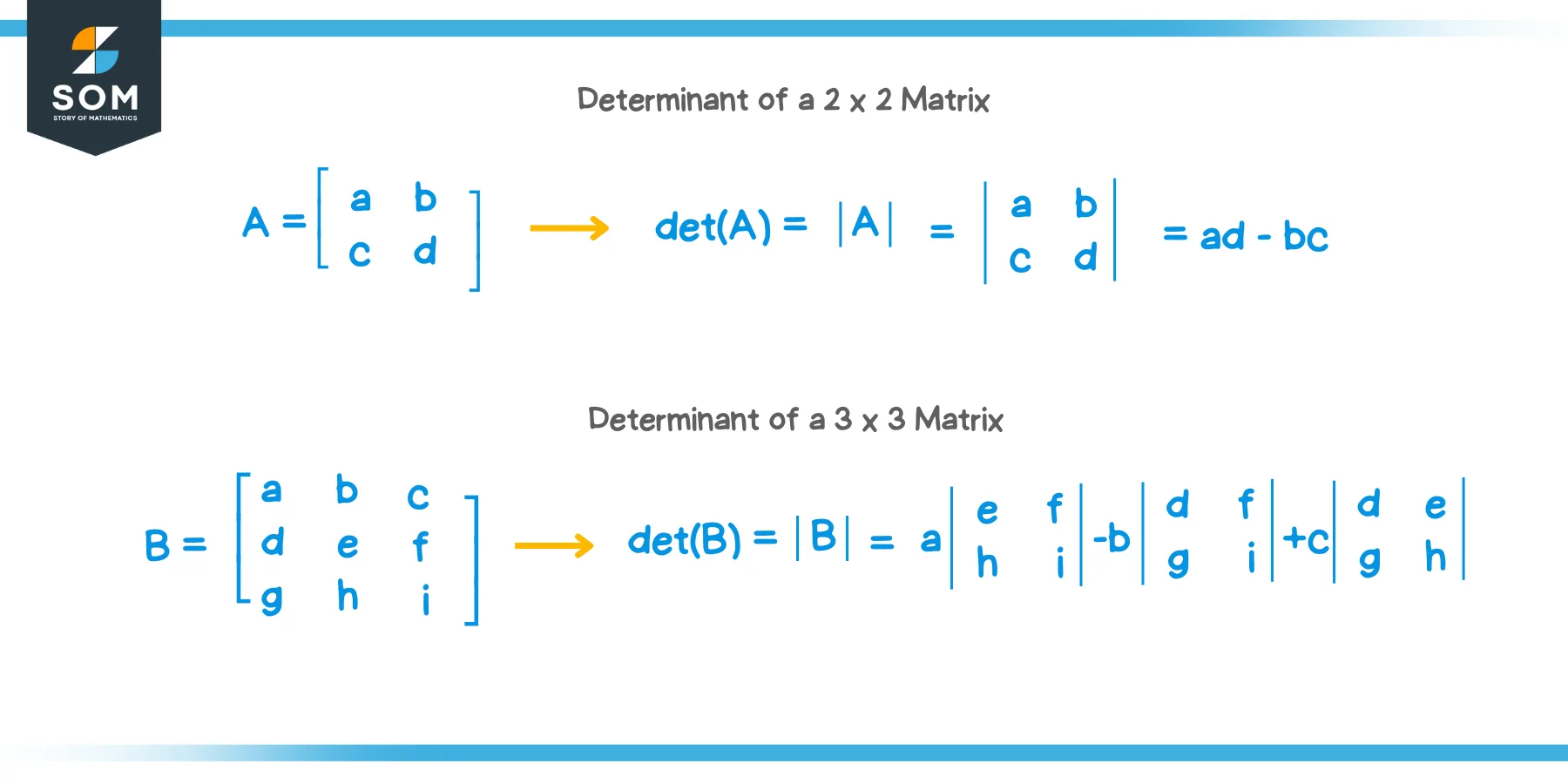

Note:

We take $ a $ and multiply it with the determinant of the $ 2 \times 2 $ matrix that is not in the row and column of $ a $
Then, we subtract the product of $ b $ and the determinant of the $ 2 \times 2 $ matrix that is not in the row and column of $ b $
Lastly, we add the product of $ c $ and the determinant of the $ 2 \times 2 $ matrix that is not in the row and column of $ c $

Using the $ 2 \times 2 $ matrix determinant formula, we can further boil down this formula into:$ det( B ) = | B | = a ( e i – f h ) – b (d i – f g ) + c (d h – e g ) $If you can’t memorize this formula (i know, it’s hard!), just remember the $ 3 $ points outlined above. Also, remember the signs of the scalar quantities that you multiply each determinant with. $ a $ is positive, $ b $ is negative, and $ c $ is positive.Now, consider the $ 3 \times 3 $ matrix shown below:$ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $Let’s calculate the determinant of this matrix using the formula we just learned. Shown below: $ B = \begin{bmatrix} { 1 } & { 2 } & { – 1 } \\ { 0 } & { 3 } & { – 4 } \\ { – 1 } & { 2 } & { 1 } \end {bmatrix} $ $ det( B ) = | B | = 1 [ ( 3 )( 1 ) – ( – 4 )( 2 ) ] – 2 [ ( 0 )( 1 ) – ( – 4 )( – 1 ) ] + (-1) [ ( 0 )( 2 ) – ( 3 )( – 1 ) ] $ $ = 1 [ 3 + 8 ] – 2 [ 0 – 4 ] + (-1) [ 0 + 3 ] $ $ = 1 [ 11 ] – 2[ – 4 ] – 1[ 3 ] $ $ = 11 + 8 – 3 $ $ = 16 $The determinant of the $ 3 \times 3 $ matrix $ B $ is $ 16 $.Let’s take a look at more examples to enhance our understanding of determinants!

Example 1

Given $ C = \begin{bmatrix} { – 9 } & { – 2 } \\ { 3 } & { – 1 } \end {bmatrix} $, find $ | C | $. SolutionWe have to find the determinant of the $ 2 \times 2 $ matrix shown above. Let’s use the formula and find the determinant. Shown below:$ det( C ) = | C | = \begin{vmatrix} { – 9 } & { – 2 } \\ { 3 } & { – 1 } \end {vmatrix} $$ = ( – 9 ) ( – 1 ) – ( – 2 ) ( 3 ) $$ = 9 + 6 $$ = 15 $

Example 2

Find $ x $ given $ \begin{vmatrix} { 1 } & { x } \\ { 8 } & { 2 } \end {vmatrix} = 34 $. SolutionWe are already given the determinant and have to find an element, $ x $. Let’s put it into the formula and solve for $ x $:$ \begin{vmatrix} { 1 } & { x } \\ { 8 } & { 2 } \end {vmatrix} = 34 $$ ( 1 ) ( 2 ) – ( x ) ( 8 ) = 34 $$ 2 – 8x = 34 $$ -8x = 34 – 2 $$ – 8x = 32 $$ x = – 4 $

Example 3

Calculate the determinant of Matrix $ D $ shown below:$ D = \begin{bmatrix} { 6 } & { 2 } \\ { – 12 } & { – 4 } \end {bmatrix} $Solution We will use the formula to calculate the determinant of Matrix $ D $. Shown below:$ det( D ) = | D | = \begin{vmatrix} { 6 } & { 2 } \\ { – 12 } & { – 4 } \end {vmatrix} $$ = ( 6 ) ( – 4 ) – ( 2 ) ( – 12 ) $$ = -24 + 24 $$ = 0 $The determinant of this matrix is $ 0 $!This is a special type of matrix. It is a non-invertible matrix and is known as a singular matrix. To learn more, check here.

Practice Questions

Find the determinant of the matrix shown below: $ A = \begin{bmatrix} – 5 & – 10 \\ 3 & – 1 \end{bmatrix} $
Find $ y $ given $ \begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \end {vmatrix} = – 60 $

Answers

Matrix $ A $, a $ 2 \times 2 $ matrix, is given. We need to find the determinant of it. We do so by applying the formula. Process is shown below:$ det( A ) = | A | = \begin{vmatrix} { – 5 } & { – 10 } \\ { 3 } & { – 1 } \end {vmatrix} $$ = ( – 5 ) ( – 1 ) – ( – 10 ) ( 3 ) $$ = 5 + 30 $$ = 35 $
We are already given the determinant and have to find an element, $ y $. Let’s put it into the formula for the determinant of a $ 3 \times 3 $ matrix and solve for $ y $:$ \begin{vmatrix} { 1 } & { 3 } & { – 1 } \\ { 5 } & { 0 } & { y } \\ { – 1 } & { 2 } & { 3 } \end {vmatrix} = – 60 $ $ 1 [ ( 0 )( 3 ) – ( y )( 2 ) ] – 3 [ ( 5 )( 3 ) – ( y )( – 1 ) ] + (-1) [ ( 5 )( 2 ) – ( 0 )( – 1 ) ] = – 60$ $ 1 [- 2y ] – 3 [ 15 + y ] + (-1) [ 10 ] = – 60 $ $ – 2y – 45 – 3y – 10 = – 60 $ $ – 5y – 55 = – 60 $ $ – 5y = – 60 + 55 $ $ – 5y = – 5 $ $ y = 1 $