Double Integrals in Polar Coordinates – Definition, Formula, and Examples

Double integrals in polar coordinates are a great help when we want to evaluate iterated integrals, particularly double integrals, of expressions that involve circular regions. Being comfortable working with polar coordinates, in general, is important if we want to explore a wide range of topics in math and applied sciences. This is why we must know how to integrate expressions by converting them into polar coordinates. 

Double integrals in polar coordinates are important when we want to evaluate complex expressions that will benefit from polar coordinate conversion. Knowing how to work with double integrals involving polar coordinates allows us to convert expressions and integrate them using simpler methods.

In this article, we’ll show you regions such as disks, rings, and combinations of these that benefit from using double integrals in polar coordinates instead of Cartesian coordinates.  We’ll also show you how to evaluate double integrals once we have them in polar coordinate forms.  You must be familiar with polar coordinates and integral properties at this point, but don’t worry, we’ve linked important resources in case you need a refresher!

How To Convert Double Integral to Polar Coordinates?           

We can convert double integral to polar coordinates by rewriting $\int \int_R f(x, y) \phantom{x}dA$ as $\int \int_{R} f(r \cos \theta, r \sin \theta) \phantom{x}r \phantom{x}dr d\theta$. This method is important when we want to integrate expressions that represent regions involving circles such as the ones shown below.

First, let’s take a quick refresher on how we convert Cartesian to polar coordinate and expressions. This skill is essential if we want to understand the more detailed process of how we convert double integrals to polar coordinates. When we’re given a Cartesian coordinate, $(x,y )$, we can convert this to polar coordinate, $(r, \theta)$:

\begin{aligned} x &= r \cos \theta \\ y &= r \sin \theta \end{aligned}

Now, we want to convert the polar coordinate, $(r, \theta)$, to its Cartesian form using the equations below.

\begin{aligned} r &= \sqrt{x^2 + y^2}\\ \theta &= \tan^{-1} \left(\dfrac{y}{x}\right) \end{aligned}

We can use these equations to also rewrite expressions from one form to another. Here are some equivalent equations showing both their polar and Cartesian forms.

Try converting these examples from their Cartesian forms back to the polar forms to double-check your knowledge of polar coordinates. If you need a further refresher on this topic, head over to this link. For now, let’s establish the definition of double integrals in polar coordinates.

This means that if we want to convert double integrals to polar coordinates, we’ll have to convert the function we’re integrating, the limits of the region we’re integrating, and the differential expression. We’ve broken down the steps for you:

• Convert the function and limits of integration by using the polar coordinate formulas shown below.

\begin{aligned} x &= r \cos \theta \\ y &= r \sin \theta\\r^2 &= x^2 + y^2 \end{aligned}

• Rewrite the rectangular differential, $dA = dy dx$, to its polar form.

\begin{aligned}dA= r dr d\theta\end{aligned}

• Use the converted expressions to rewrite the entire double integral to its polar form.

\begin{aligned}\int \int_R f(x,y) \phantom{x}dydx &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\end{aligned}

Once we’ve converted the double integral from the Cartesian form to its polar form, evaluate the double integral in its polar form. One of the trickiest parts of the steps in converting double integrals to polar coordinates is finding the double integral’s limits of integration in polar form. This is why we’ve prepared a special section for the process of finding the limits of double integrals in polar form.

How To Find Limits of Double Integrals in Polar Coordinates?               

As we have mentioned, we can use the polar forms of $x$ and $y$ to find the limits of double integrals in polar coordinates.

\begin{aligned}x &= r \cos \theta\\ y &= r \sin \theta\end{aligned}

Using these polar forms, we can solve for the values of $r$ and $\theta$.  We can also rewrite the limits of integrations in polar coordinates by first sketching the region representing the function we’re representing.

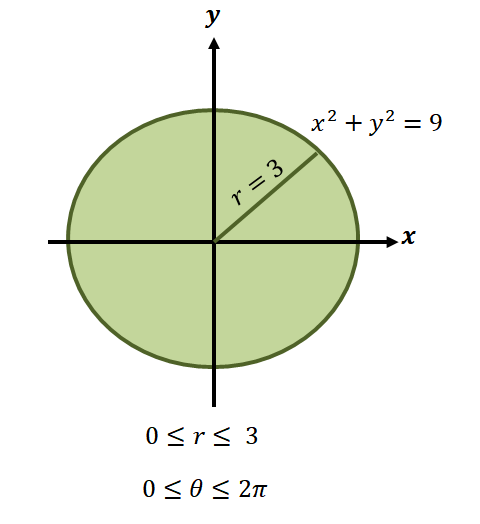
As we have mentioned, the regions of these functions normally involve circles, so we’ll need to identify the range of $\theta$ and $r$ covered by the region.

\begin{aligned}\int \int_R f(x,y) \phantom{x}dydx &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\end{aligned}

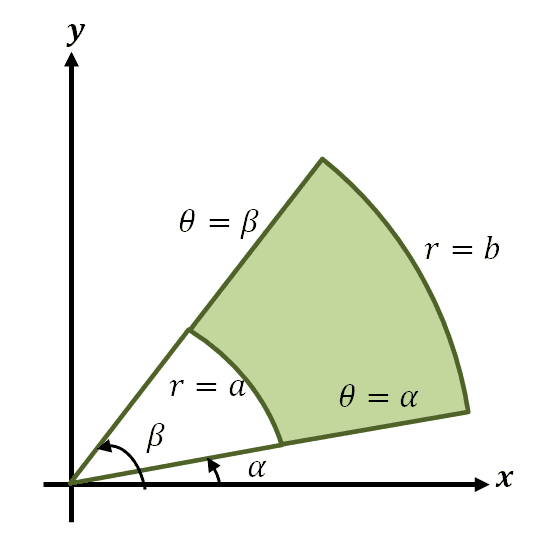
Suppose that we have the following sets of domain for $r$ and $\theta$ covering the region, $R$:

\begin{aligned}a \leq r \leq b\\\alpha \leq \theta \leq \beta\end{aligned},

we can write the limits of integration as $\int_{\theta_1 = \alpha}^{\theta_2 = \beta} \int_{r_1 (\theta) = a}^{r_2 (\theta) = b}$.

Now, for the circular region represented by the equation, $x^2 + y^2 =9$, the limits for the radius range from $0$ to $3$ units. Since the region covers one complete revolution, we have $0 \leq \theta \leq 2\pi$. This is why we have the function’s limits of integration in polar form as $\int_{\theta_1 =0}^{\theta_2 = 2\pi} \int_{0 = a}^{r_2 (\theta) = 3}$.

There are instances when finding the expression for the function in polar form is not as straightforward. The graph above is an example of more complex regions and we can evaluate their double integral by setting up the limits of integrations as shown below.

As can be seen from the general form, we simply evaluate the differential of $r$ by using the limits of integration in terms of $\theta$ for the radii. The process will be similar to integrating double integrals with irregularly-shaped regions.

Of course, practice is still the best way to know the process of working on double integrals in polar coordinates. This is why we’ll show you two examples first to highlight the process of converting double integrals in polar coordinates to evaluating the resulting double integral!

Examples of Converting Double Integral to Polar Coordinate    

We’ve prepared two examples to show you the complete process of converting and evaluating double integral polar coordinates: 1) one with a simpler circular region and 2) a double integral with a more complex region for its area.

\begin{aligned}\int_{0}^{2} \int_{0}^{\sqrt{4 – x^2}} (x^2 + y^2) \phantom{x}dy dx\end{aligned}

Now, let’s inspect the components of the double integral shown above and see the shape formed by the double integral’s region.

\begin{aligned} \int_{0}^{2} \int_{0}^{\sqrt{4 – x^2}} (x^2 + y^2) \phantom{x}dy dx &= \int \int_R (x^2 + y^2) \phantom{x}dA\end{aligned}

From this, we can see that $R$ is a sector of a circle with a radius of $2$ units. Now, to find the limits for $r$ and $\theta$, let’s use the fact that $x = r \cos \theta$ and $y = r \sin \theta$. We can see from the limits of $y$ that the region is bounded $y = 0$ and $y = \sqrt{4 – x^2}$ is a sector of a circle with a radius of $2$ units.

 We can confirm this by equating each pair of limits from the Cartesian form of the double integral to solve for the values $\theta$.

From the semi-circular region, we can see that the value of $\theta$ is from $\theta = 0$ to $\theta = \pi$.This also shows that sketching the region first using the limits from $y$ will make the process of finding the double integrals’ limits in polar coordinates much easier. Hence, we have $0 \leq \theta \leq \pi$ and $0 \leq r \leq 2$.

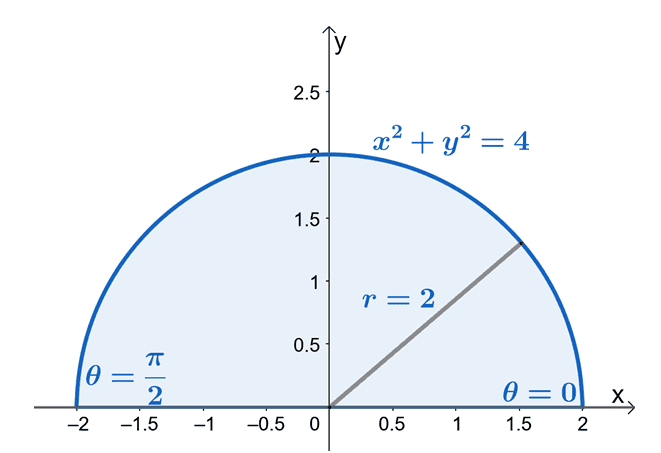
Let’s now rewrite $f(x,y )$ to its polar form and apply the Pythagorean identity, $\sin^2 \theta + \cos^2 \theta = 1$ to further simplify the expression.

\begin{aligned}x^2 + y^2 &= (r\cos \theta)^2 + (r \sin \theta)^2\\&= r^2 \cos^2 \theta + r^2 \sin^2\theta\\&= r^2(\cos^2 \theta + \sin^2 \theta)\\&= r^2(1)\\&= r^2\end{aligned}

Combine these two pieces of information to rewrite our double integral to its polar form.

\begin{aligned}\int \int_R f(x, y)\phantom{x}dA &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\\\\\int_{0}^{1} \int_{0}^{\sqrt{4 – x^2}} (x^2 + y^2) \phantom{x}dy dx &= \int_{0}^{\pi/2} \int_{0}^{2} r^2 \phantom{x} rdr d\theta\\&= \int_{0}^{\pi/2} \int_{0}^{2} r^3 \phantom{x} dr d\theta\end{aligned}

Do you see the beauty of double integrals in polar coordinates? We’re now left with a simpler expression to integrate. Apply the power rule to integrate $r^3$ with respect to $r$ first.

\begin{aligned}\int_{0}^{2} r^3 \phantom{x} drd\theta&= \int_{0}^{\pi/2} \left[\int_{0}^{2} r^3 \phantom{x} dr \right ] d\theta\\&= \int_{0}^{\pi/2} \left[\dfrac{r^4}{4}\right ]_{0}^{2} \phantom{x}d\theta\\&= \int_{0}^{\pi/2} \left(\dfrac{2^4}{4} – \dfrac{0^4}{4} \right ) \phantom{x}d\theta\\&= \int_{0}^{\pi/2} 4  \phantom{x}d\theta\end{aligned}

Evaluate the resulting expression with respect to $\theta$ this time.

\begin{aligned}\int_{0}^{\pi/2} 4  \phantom{x}d\theta &= [4 \theta]_{0}^{\pi/2}\\&=4 \left(\dfrac{\pi}{2} – 0\right)\\&= 2\pi\end{aligned}

This means that $\int_{0}^{2} \int_{0}^{\sqrt{4 – x^2}} (x^2 + y^2) \phantom{x}dy dx$ is equal to $2\pi$. By integrating the double integral in its polar form, we’re left with simpler expressions to work on – making this part of the process much easier!

Now, let’s try a more complex example: integrating the double integral, $\int_{0}^{1} \int_{0}^{x} y \sqrt{x^2 + y^2} \phantom{x}dydx$.   Let’s first rewrite the function in its polar form using the same set of equations from before.

We can see that the limits of $x$ are from $0$ to $1$ while that of $y$ are from $0$ to $x$. In Cartesian form, we can see that the region of integration is bounded by: $R = \{(x, y) | 0 \leq x \leq 1, 0 \leq y \leq x\}$.

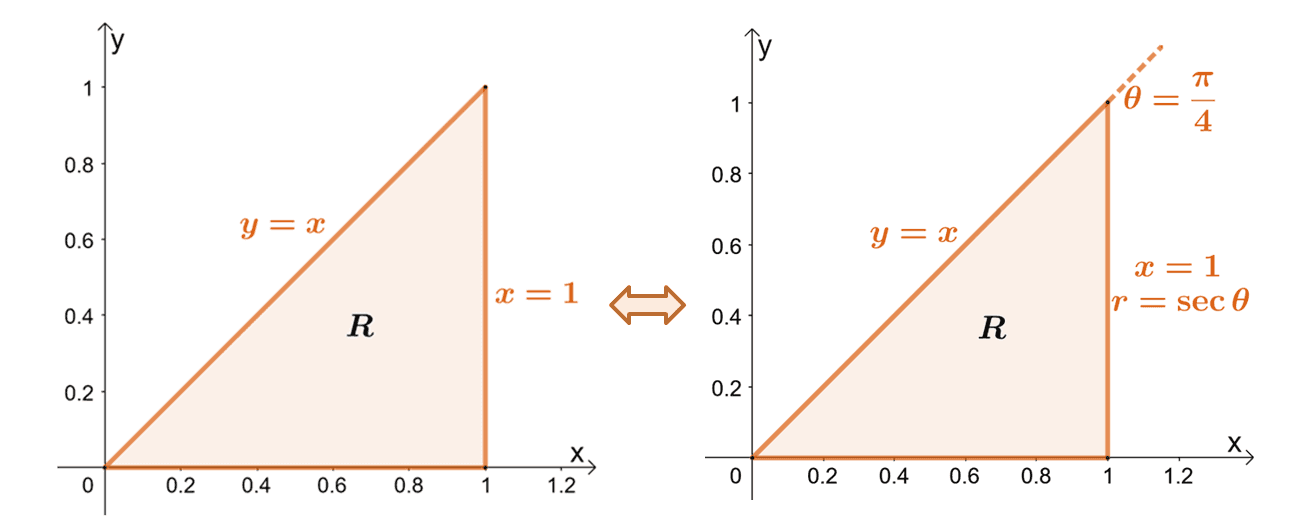
Let’s now convert the limits of integration by equating the limits of $x$ to $r \cos \theta$ and $y$ to $r \sin \theta$. This will help us understanding the graph shown on the right.

These expressions for $r$ and $\theta$ represent the limits of integration of our double integral in double integrals.

\begin{aligned}R &= \left\{(r, \theta)| 0 \leq \theta \leq \dfrac{\pi}{4}, 0 \leq r \leq \dfrac{1}{\cos \theta}\right\} \end{aligned}

Now that we have our expressions for $f(x,y) \phantom{x}dA$ and limits of integrations in polar form, it’s time for us to rewrite our double integral to polar form.

\begin{aligned}\int \int_R f(x, y)\phantom{x}dA &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\\\\\int_{0}^{1} \int_{0}^{x} y\sqrt{x^2 + y^2}\phantom{x}dy dx &= \int_{0}^{\pi/4} \int_{0}^{1/\cos \theta} r^2\sin\theta \phantom{x} rdr d\theta\\&= \int_{0}^{\pi/4} \int_{0}^{1/\cos \theta} r^3\sin \theta \phantom{x} dr d\theta\end{aligned}

From a complex expression such as $y\sqrt{x^2 + y^2}$ in Cartesian form, it’s now easier to evaluate the double integral – $\int_{0}^{\pi/4} \int_{0}^{1/\cos \theta} r^3\sin \theta \phantom{x} dr d\theta$. We begin by integrating the expression with respect to $r$ first and treating $\theta$ as a constant first.

\begin{aligned}\int_{0}^{\pi/4} \int_{0}^{1/\cos \theta} r^3\sin \theta \phantom{x} dr d\theta &= \int_{0}^{\pi/4} \left[\int_{0}^{1/\cos \theta} r^3\sin \theta \phantom{x} dr\right ]d\theta\\&= \int_{0}^{\pi /4}\left[ \sin \theta \int_{0}^{1/\cos \theta} r^3\phantom{x} dr\right ]d\theta\\&= \int_{0}^{\pi /4}\sin \theta \left[\dfrac{r^4}{4} \right ]_{0}^{1/\cos \theta}d\theta\\&= \int_{0}^{\pi/4} \sin \theta \left(\dfrac{1}{\cos^4 \theta} \cdot \dfrac{1}{4} – 0 \right ) \phantom{x}d\theta\\&= \dfrac{1}{4}\int_{0}^{\pi/4} \dfrac{\sin \theta}{\cos^4 \theta}  \phantom{x}d\theta\end{aligned}

Apply the method of u-substitution to integrate the resulting expression with respect to $\theta$. Let’s disregard the limits of integration for now so we can focus on integrating the expression.

\begin{aligned}u &= \cos \theta\\du &= -\sin \theta \phantom{x}d\theta\\\\\int \dfrac{\sin \theta}{\cos^4 \theta} \phantom{x}d\theta &= \int \dfrac{\sin \theta}{\cos^4 \theta} \cdot \dfrac{du}{-\sin \theta }\\&= \int -\dfrac{1}{u^4} \phantom{x}du\\&= -\int u^{\displaystyle{-4}} \phantom{x}du\\&= -\dfrac{u^{\displaystyle{-4 + 1}}}{-4 + 1} \phantom{x}du\\&= \dfrac{1}{3u^3}\\&= \dfrac{1}{3\cos^3 \theta} \end{aligned}

Evaluate the resulting expression from $\theta = 0$ to $\theta = \dfrac{\pi}{4}$.

\begin{aligned}\int_{0}^{\pi /4} \dfrac{\sin \theta}{\cos^4 \theta} \phantom{x}d\theta &= \left[ \dfrac{1}{3\cos^3 \theta} \right ]_{0}^{\pi /4}\\&= \dfrac{1}{3}\left(\dfrac{1}{\cos^3 \dfrac{\pi}{4}} – \dfrac{1}{\cos^3 0}  \right )\\&= \dfrac{1}{3} \left(\dfrac{1}{(1/ \sqrt{2})^3} – 1 \right)\\&= \dfrac{1}{3}(2\sqrt{2} – 1)\end{aligned}

By converting the double integral, $\int_{0}^{1} \int_{0}^{x} y \sqrt{x^2 + y^2} \phantom{x}dydx$, to its polar form, $\int_{0}^{\pi/4} \int_{0}^{1/\cos \theta} r^3\sin \theta \phantom{x} dr d\theta$ and evaluate it instead. In fact, we’ve shown that the double integral’s value is equal to $\dfrac{2\sqrt{2} – 1}{3}$ or approximately equal to $0.152$.

These examples showcase the importance of converting double integrals to polar coordinates – especially when you’re working with regions that involve disks, rings, and regions involving circles. We’ve prepared more examples for you to work on so that by the end of the next section, you’re already confident with double integrals in polar coordinates!

Example 1

Evaluate the integral, $\int \int_R 6x \phantom{x}dA$, over the region bounded by the following limits: $\{1 \leq r \leq 4, 0 \leq \theta \leq \pi\}$.

Solution

From the limits of integration, we can see that our region is formed by two circles formed by two radii: $1$ unit and $4$ units. Since $0 \leq \theta \leq \pi$, we’re expecting the region to be a semicircle lying above the $x$-axis.

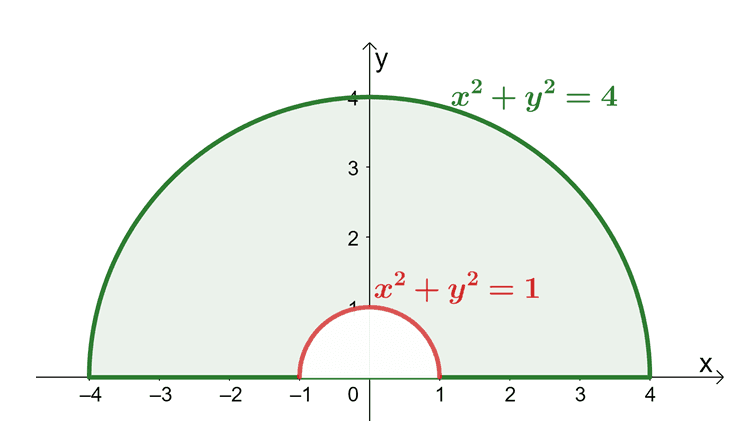
The shaded region represents $dA$, so now, let’s rewrite $6x$ in their polar form using the fact that $x = r \cos \theta$.

\begin{aligned}66x &= 6(r \cos \theta)\\&= 6r \cos \theta\end{aligned}

 Set up the double integral now that we have both the limits of integration as well as the function in polar forms.

\begin{aligned}\int \int_R f(x, y)\phantom{x}dA &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\\\\\int\int 6x \phantom{x}dy dx &= \int_{0}^{\pi} \int_{1}^{4} (6r \cos \theta) \phantom{x} rdr d\theta\\&= \int_{0}^{\pi} \int_{1}^{4} 6r^2 \cos \theta \phantom{x} dr d\theta\end{aligned}

Now, integrate the expression with respect to $r$ first and by treating $\theta$ as a constant.

\begin{aligned}\int_{0}^{\pi} \int_{1}^{4} 6r^2 \cos \theta \phantom{x} dr d\theta &=\int_{0}^{\pi} \left[\int_{1}^{4} 6r^2 \cos \theta \phantom{x} dr \right ] d\theta\\&=\int_{0}^{\pi} \left[\int_{1}^{4} 6r^2 \cos \theta \phantom{x} dr \right ] d\theta\\&= \int_{0}^{\pi} \cos \theta \left[\int_{1}^{4} 6r^2 \phantom{x} dr \right ] d\theta\\&= \int_{0}^{\pi} \cos \theta \left[\dfrac{6r^3}{3} \right ]_{1}^{4} d\theta \\&= \int_{0}^{\pi} \cos \theta (2\cdot 2^3 – 2\cdot 1^3) d\theta \\&= 14\int_{0}^{\pi} \cos \theta d\theta \end{aligned}

Continue to simplify the expression by evaluating the integral with respect to $\theta$ from $\theta = 0$ to $\theta = \pi$.

\begin{aligned}14\int_{0}^{\pi} \cos \theta d\theta &= 14 \left[\sin \theta \right ]_{0}^{\pi}\\&= 14(\sin \pi – \sin 0)\\&= 0 \end{aligned}

This shows that the resulting double integral is equal to $0$.

Example 2

Evaluate the integral, $\int \int_R e^{x^2 + y^2} \phantom{x}dA$, over the region, $R$. Keep in mind that $R$ represents a unit disk that is centered at the origin.

Solution

The region we’re working with is a unit disk, so this is a circular region with a radius of $1$ unit.

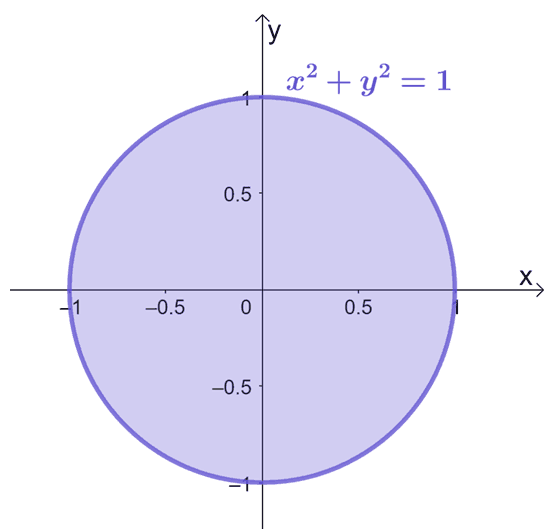
From this, we can see that the limits of $R$ are the following: $0 \leq \theta 2\pi$ and $0 \leq r \leq 1$. Let’s now rewrite $e^{x^2 + y^2}$ in its polar form using the following equations: $x = r \cos \theta$ and $y = r \sin \theta$.

\begin{aligned}x^2 + y^2 &= r^2 \cos^2 \theta + r^2 \sin^2 \theta\\&= r^2(\cos^2 \theta + \sin^2 \theta)\\&= r^2 (1)\\&= r^2\\\\e^{x^2 + y^2} &= e^{r^2}\end{aligned}

Now that we have all the necessary components in polar form, let’s now rewrite the double integral in its polar form.

\begin{aligned}\int \int_R f(x, y)\phantom{x}dA &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\\\\\int\int e^{x^2 + y^2} \phantom{x}dy dx &= \int_{0}^{2\pi} \int_{0}^{1} e^{r^2}\phantom{x} rdr d\theta\\&= \int_{0}^{2\pi} \int_{0}^{1} re^{r^2}\phantom{x} dr d\theta\end{aligned}

We apply the substitution method to integrate the expression with respect to $r$ while we keep $\theta$ a constant.

\begin{aligned}u &= r^2\\du &= 2r \phantom{x}dr\\\dfrac{1}{2r} \phantom{x} du &= dr\\\int_{0}^{1} re^{r^2}\phantom{x} dr &= \int_{0}^{1} \dfrac{1}{2} e^u \phantom{x}du\\&= \dfrac{1}{2}\left[e^u \right ]_{0}^{1}\\&= \dfrac{1}{2}(e – 1)\\\\\int_{0}^{2\pi} \int_{0}^{1} re^{r^2}\phantom{x} dr d\theta &= \int_{0}^{2\pi} \left[\int_{0}^{1} re^{r^2}\phantom{x} dr \right ] d\theta\\&= \int_{0}^{2\pi}\dfrac{1}{2}(e – 1) \phantom{x}d\theta \end{aligned}

We continue by integrating the expression with respect to $\theta$ this time.

\begin{aligned}\int_{0}^{2\pi}\dfrac{1}{2}(e – 1) \phantom{x}d\theta &= \left[\dfrac{1}{2}(e – 1)\theta\right]_{0}^{2 \pi}\\&= \dfrac{1}{2}(e – 1)[\theta]_{0}^{2\pi}\\&= \pi(e – 1) \end{aligned}

This means that the double integral is equal to $\pi(e – 1)$ or approximately equal to $5.40$.

Example 3

Evaluate the double integral, $\int_{-1}^{1} \int_{-\sqrt{1 – x^2}}^{0} \sin(x^2 + y^2) \phantom{x}dydx$, by converting it to polar form first.

Solution

We can see that evaluating this integral in Cartesian form is close to impossible – this is why rewriting it in polar form is such a crucial step. From the upper limit of $y$, the region we’re working with is a semicircle located below the $x$-axis.

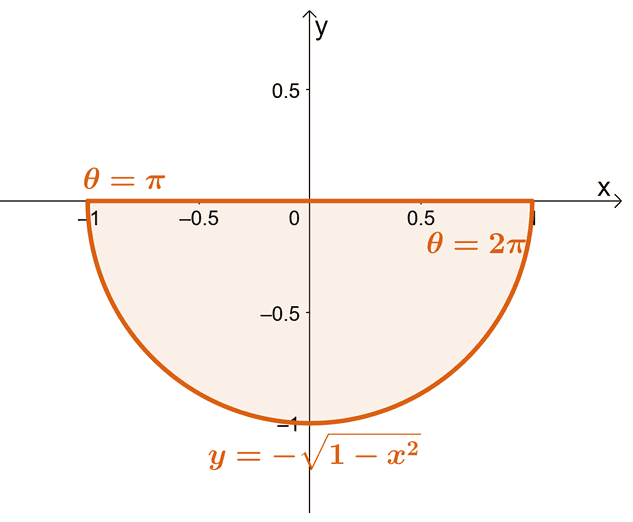
We can also double-check the limits of integrations’ values by equation equating each pair of values to $x = r\cos \theta$ and $y = r \sin \theta$ as shown below.

These limits of integrations in polar form confirms the fact that our region is a semicircle located below the $x$-axis. Next, convert $dA$ and $\sin(x^2 + y^2)$ to their polar forms by simplifying $x^2 + y^2$ to $r^2$.

\begin{aligned}dA &= r \phantom{x}dr d\theta\\\sin(x^2 + y^2) &= \sin(r^2 \sin^2\theta + r^2 \cos^2\theta)\\&=\sin r^2\end{aligned}

Now that we have all the key components to write our double integral in polar form, it’s time for us to write the double integral in polar form. Use the general form as guide when translating our double integral from Cartesian to polar form.

\begin{aligned}\int \int_R f(x, y)\phantom{x}dA &= \int_{\theta_1}^{\theta_2} \int_{r_1 (\theta)}^{r_2 (\theta)} f(r\cos \theta, r\sin \theta) \phantom{x} rdr d\theta\\\\\int\int \sin(x^2 + y^2) \phantom{x}dy dx &= \int_{\pi}^{2\pi} \int_{0}^{1} \sin(r^2)\phantom{x} rdr d\theta\\&= \int_{\pi}^{2\pi} \int_{0}^{1} r(\sin r^2)\phantom{x} dr d\theta\end{aligned}

Integrate the resulting expression with respect to $r$ and treating the rest of the constants and variable constant.

\begin{aligned}u &= r^2\\du &= 2r \phantom{x}dr\\\dfrac{1}{2r} \phantom{x} du &= dr\\\int_{0}^{1} r\sin r^2\phantom{x} dr &= \int_{0}^{1} \dfrac{1}{2} \sin u \phantom{x}du\\&= \dfrac{1}{2}\left[- \cos u \right ]_{0}^{1}\\&= -\dfrac{1}{2}(\cos 1 – \cos 0)\\&= -\dfrac{1}{2}(\cos 1 – 1)\\\\\int_{\pi}^{2\pi} \int_{0}^{1} r\sin r^2\phantom{x} dr d\theta &= \int_{\pi}^{2\pi} \left[\int_{0}^{1} r\sin r^2\phantom{x} dr \right ] d\theta\\&= \int_{\pi }^{2\pi}-\dfrac{1}{2}(\cos 1 – 1) \phantom{x}d\theta \end{aligned}

Continue by integrating the resulting single integral with respect to $\theta$ then evaluate the expression from $\theta  = \pi$ to $\theta = 2\pi$.

\begin{aligned}\int_{\pi}^{2\pi}-\dfrac{1}{2}(\cos 1 – 1) \phantom{x}d\theta &= -\dfrac{1}{2}(\cos 1 – 1)\int_{0\pi}^{2\pi} \phantom{x}d\theta \\&= -\dfrac{1}{2}(\cos 1 – 1)\left[\theta\right]_{\pi}^{2\pi}\\&= \dfrac{1}{2}(1 – \cos 1)(2\pi – \pi)\\&= \dfrac{\pi}{2}(1 – \cos 1)\end{aligned}

This shows that $\int_{-1}^{1} \int_{-\sqrt{1 – x^2}}^{0} \sin(x^2 + y^2) \phantom{x}dydx$ is equal to $\dfrac{\pi}{2}(1 – \cos 1)$ or approximately equal to $0.72$.

Practice Questions

1. Evaluate the integral, $\int \int_R 3x \phantom{x}dA$, over the region bounded by the following limits: $\{1 \leq r \leq 2, -\dfrac{\pi}{2} \leq \theta \leq \dfrac{\pi}{2}\}$.
2. Evaluate the integral, $\int \int_R \sin (x^2 + y^2) \phantom{x}dA$, over the region, $R$. Keep in mind that $R$ represents a quadrant of a unit circle and is centered at the origin.
3. Evaluate the double integral, $\int_{-1}^{1} \int_{-\sqrt{1 – x^2}}^{0} e^{x^2 + y^2} \phantom{x}dydx$, by converting it to polar form first.
4. Evaluate the integral, $\int \int_R r^2 \cos \theta r\phantom{x}r dr d\theta$, over the region, $R$. Keep in mind that $R$ is from the cardiod, $r = 1+ \sin \theta$, and bounded by the positive sides of the pole and the polar axis.
5. Evaluate the integral, $\int \int_R \sqrt{1 + 3x^2 + 3y^2}\phantom{x} dA$, over the region, $R$. Keep in mind that $R$ is the bottom half of $x^2 + y^2 = 9$.

Answer Key

1.$ \int_{-\pi/2}^{\pi / 2} \int_{1}^{2} 3r \cos \theta r \phantom{x}dr d\theta = 14$
2. .$ \int_{0}^{\pi / 2} \int_{0}^{1} (\sin r^2)r \phantom{x} dr d\theta = \dfrac{\pi}{4}(1 – \cos 1) \approx 0.36$
3. $\int_{\pi}^{2\pi} \int_{0}^{1} re^{r^2} \phantom{x}drd\theta = \pi e + \dfrac{\pi \left(-e-1\right)}{2} \approx 2.70$
4.$\int_{0}^{\pi/2} \int_{0}^{1 + \sin \theta} r^3 \cos \theta \phantom{x}dr d\theta = \dfrac{31}{20}$
5. $\int_{\pi}^{2\pi } \int_{0}^{3} r\sqrt{1 + 9r^2} \phantom{x}dr d\theta = \dfrac{\pi \left(82\sqrt{82} – 1\right)}{27} \approx 86.28$

Images/mathematical drawings are created with GeoGebra.