Equation of a Plane – Definition, General Forms, and Examples

Learning about the equation of a plane allows us to understand and visualize a plane’s behavior in a three-dimensional coordinate system. Planes are one of the simplest curves you’ll encounter. This is why understanding the equation of the plane is important if we want to dive into equations of more complex curves and surfaces later.The equation of a plane in a three-dimensional coordinate system is determined by the normal vector and an arbitrary point that lies on the plane. The equation of a plane can be written in its vector and scalar forms.In this article, we’ll know the key components in constructing a plane in $\mathbb{R}^3$. We’ll explore the different components and properties that can be observed of a plane and its equation in the 3D coordinate system.We’ll need our knowledge on 3D coordinate systems and equations of the line in $\mathbb{R}^3$, so keep your notes on these topics handy for a quick refresher. For now, let’s dive right into the basics of the equation of a plane!

What Is the Equation of a Plane?

The equation of plane in $\mathbb{R}^3$ is defined by a normal vector, $\textbf{n}$, and a given point, $P_o(x_o y_o, z_o)$ that lies on the plane. The equation of a plane can be written using its vector and scalar components.\begin{aligned}\phantom{xxx}\textbf{VECTOR EQUATION}&\textbf{ OF A PLANE}\phantom{xxx}\\\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) &= 0\\\textbf{n}\cdot \textbf{r} &=\textbf{n}\cdot \textbf{r}_o \\\\\phantom{xxx}\textbf{SCALAR EQUATION}&\textbf{ OF A PLANE}\phantom{xxxxx}\\a(x – x_o) + b(y – y_o) &+ c(z – z_o) =0\end{aligned}We’ll discuss how these general forms came to be. In our discussion on the equation of the line, we’ve learned that we can define a line in $\mathbb{R}^3$ by using a point and a vector to indicate direction. Now that planes contain lines with different directions, using parallel vectors won’t be that much of a help. 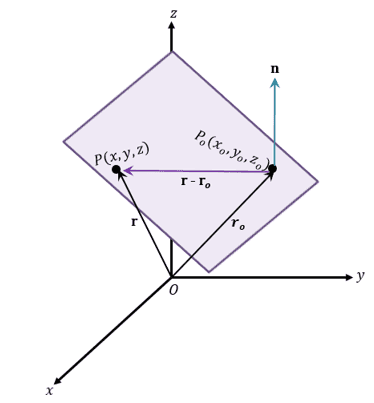Instead, we use a vector, $\textbf{n}$, that is perpendicular to the plane and we call this the normal vector.Here’s an example of a plane that lies in a three-dimensional plane. From this, we can see that the plane can be defined by the arbitrary point, $P_o(x_o, y_o, z_o)$, and a normal vector, $\textbf{n}$. Utilizing the normal vector allows us to highlight the relationship between the plane and $\textbf{n}$: all the vectors lying on the plane are also perpendicular to the normal vector.The vector, $\overrightarrow{P_oP} = \textbf{r} – \textbf{r}_o$, lies on the plane, so the normal vector will also be perpendicular with it. Recall that when two vectors are normal to each other, their dot product is equal to zero. Hence, we have the following equations:\begin{aligned}\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) &= 0 \phantom{xxxxx}(1)\\\\\textbf{n}\cdot \textbf{r}  – \textbf{n}\cdot \textbf{r}_o &= 0\\ \textbf{n}\cdot \textbf{r} &=\textbf{n}\cdot \textbf{r}_o \phantom{xx}(2)\end{aligned}These equations are what we call the vector equations of a plane.Now, let’s use the components of each of these vectors to write the scalar form of the plane’s equation.\begin{aligned}\textbf{n} &= <a, b , c> \\\textbf{r} &=<x, y, z> \\\textbf{r}_o &= <x_o, y_o, z_o>\end{aligned}Substitute these into $\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) = 0$.\begin{aligned}\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) &= 0\\<a, b, c> \cdot (<x, y, z> – <x_o, y_o, z_o>)&= 0\\<a, b, c> \cdot &= 0\\a(x – x_o) + b(y – y_o) + c(z – z_o) &= 0\end{aligned}If we let $d$ represent the sum of the constants, $-ax_o$, $-by_o$, and $-cz_o$, we’ll have $d = -(ax_o + by_o + cz_o)$ and a simplified linear equation shown below.\begin{aligned}ax + by + cz + d &= 0\end{aligned}This form allows us to determine the normal vector right away by inspecting the coefficients before $x$, $y$, and $z$.\begin{aligned}\textbf{n} &= <a, b, c>\end{aligned}This also means that the plane on a 3D coordinate system will have intercepts at the following:\begin{aligned}x-\text{intercept}: (x_o, 0, 0)\\y-\text{intercept}: (0, y_o, 0) \\z-\text{intercept}: (0, 0, z_o) \end{aligned}Now that we’ve covered all the fundamental concepts behind the equation of a plane, it is time that we learn how to use this definition to determine the equation of a plane.

How To Find the Equation of a Plane?

We can find the equation of plane using an arbitrary point and normal vector. When given the point, $P(x_o, y_o, z_o)$, and the normal vector, $\textbf{n} = <a, b, c>$, use their components to set up the equation of the plane in scalar form:\begin{aligned}a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\end{aligned}This means that the equation of a plane that contains the point, $(1, -4, 2)$ and the normal vector, $\textbf{n} = <2, -1, 4>$, we can write its scalar equation as shown below.\begin{aligned}(x_o, y_o, z_o) &= (1, -4, 2)\\ <a, b, c> &= <2, -1, 4>\\\\ a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\\1(x – 1) + -1(y + 4) + 4(z – 2) &= 0\\(x – 1) – (y + 4) + 4(z – 2) &= 0\end{aligned}We can further simplify the equation as shown below.\begin{aligned}x -1- y – 4 + 4z – 8 &= 0\\x- y + 4z  -13&=0 \\x- y+ 4z&= 13\end{aligned}Now, let’s take a look at what happens when we’re given three points instead.

How To Find the Equation of a Plane With 3 Points?

When given three points, $A(x_o, y_o, z_o)$, $B(x_1, y_1, z_1)$, and $C(x_2, y_2, z_2)$, we can find the equation of a plane by:

• Finding the values of the two vectors: $\overrightarrow{AB}$ and $\overrightarrow{BC}$ by subtracting the components of the vectors.

\begin{aligned}\boldsymbol{\overrightarrow{AB}}\end{aligned}	\begin{aligned}\end{aligned}
\begin{aligned}\boldsymbol{\overrightarrow{AC}}\end{aligned}	\begin{aligned}\end{aligned}

• Find a normal vector perpendicular to the plane by taking the cross product of $\overrightarrow{AB}$ and $\overrightarrow{BC}$.
• Use the resulting normal vector and either of the three points to write the equation of the plane.

For example, we can use the three points, $A = (1, -2, 0)$, $B = (3, 1, 4)$, and $C = (0, -1, 2)$, that are lying on the plane to write its equation in three-dimensional coordinate system.Since we’re given three points this time, we’ll first find the normal vector by taking the cross-product of $\overrightarrow{AB}$ and $\overrightarrow{AC}$. Find the vector components of these two vectors by subtracting their components as shown below.

\begin{aligned}\boldsymbol{\overrightarrow{AB}}\end{aligned}	\begin{aligned}\overrightarrow{AB} &= B – A \\&= <3 -1, 1 – 2, 4 – 0>\\&= <2, 3, 4>\end{aligned}
\begin{aligned}\boldsymbol{\overrightarrow{AC}}\end{aligned}	\begin{aligned}\overrightarrow{AC} &= C -A \\&= <0 -1, -1 – -2, 2 – 0>\\&= <-1, 1, 2>\end{aligned}

Let’s now take the cross product of the two vectors as shown below. The resulting cross product represents the normal vector of the plane.\begin{aligned}\textbf{n} &= \overrightarrow{AB} \times \overrightarrow{AC} \\&= \begin{vmatrix} \textbf{i} &\textbf{j} &\textbf{k} \\ 2 &3 &4 \\ -1 &1 &2 \end{vmatrix}\\&= [3\cdot 2-4\cdot 1]\textbf{i} + [4\left(-1\right)-2\cdot 2]\textbf{j} + [2\cdot 1-3\left(-1\right)]\textbf{k}\\&= 2\textbf{i} – 8\textbf{j} + 5\textbf{k}\\&= <2, -8, 5>\end{aligned}We now have $A = (1, -2, 0)$ and $\textbf{n} = <2, -8, 5>$, so use these point and vector to find the equation of the plane.\begin{aligned}(x_o, y_o, z_o) &= (1, -2, 0)\\ <a, b, c> &= <2, -8, 5>\\\\ a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\\2(x – 1)  -8(y + 2) + 5(z – 0) &= 0\\(x – 1) – (y + 4) + 4(z – 2) &= 0\end{aligned}Simplify this equation further and we’ll have $2x – 8y +5z = 18$. This shows that it’s still possible for us to find the equation of a plane given three points. Now, let’s try out more problems to master the process of writing equations of planes.Example 1Find the vector form of the equation of a plane given that both points, $A = (-4, 2, 6)$ and $B = (2, -1, 3)$, lie on the plane. We also know that the vector, $\textbf{n} = <4, 4, -1>$, is perpendicular to the plane.SolutionRecall that the vector form of the equation of the plane is as shown below.\begin{aligned}\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) &= 0\\\textbf{n}\cdot \textbf{r} &=\textbf{n}\cdot \textbf{r}_o \end{aligned}We’ll need to find the vectors, $ \textbf{r}$ and $ \textbf{r}_o$, by using the origin $O$. Assign $ \textbf{r}_o$ as $\overrightarrow{OA}$ and $ \textbf{r}$ as $\overrightarrow{OB}$.\begin{aligned}\textbf{r}_o &= \overrightarrow{OA} \\&= <-4, 2, 6>\\\\\textbf{r} &= \overrightarrow{OB} \\&= <2, -1, 3>\end{aligned}Use these vectors to write the equation of the plane in vector form.\begin{aligned}\textbf{n}\cdot (\textbf{r} – \textbf{r}_o) &= 0\\<4, 4, -1>\cdot ( <2, -1, 3> -<-4, 2, 6>)&=0\\<4, 4, -1> \cdot (<2 – -4, -1 – 2, 3 -6>)&=0\\<4, 4, -1> \cdot <6, -3, -3> &= 0\end{aligned}We can also use $\textbf{n}\cdot \textbf{r} =\textbf{n}\cdot \textbf{r}_o$ and have the equation of the plane as shown below.\begin{aligned}\textbf{n}\cdot \textbf{r} &=\textbf{n}\cdot \textbf{r}_o\\<4, 4, -1>\cdot <2, -1, 3>&=<4, 4, -1>\cdot <-4, 2, 6> \end{aligned}Example 2Determine the scalar form of the equation of the plane that contains the point $(-3, 4, 1)$ with a vector, $\textbf{n} = <2, 1, 2>$, that is perpendicular with the plane.SolutionSince we already have the point and normal vector, we can immediately use their components to find the equation of the plane.\begin{aligned}(x_o, y_o, z_o) &= (-3, 4, 1)\\ <a, b, c> &= <2, 1, 2>\\\\ a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\\2(x – -3) + 1(y – 4) + 2(z – 1) &= 0\\2(x + 3) + (y – 4) + 2(z – 1) &= 0\end{aligned}This shows the scalar form of the equation of the plane. We can also isolate all variables on the left-hand side of the equation as shown below.\begin{aligned}2x + 6 + y – 4 + 2z -2 &= 0\\2x + y + 2x &= -6 + 4 + 2\\2x+ y +2x &= 0\end{aligned}Example 3Find the equation of the plane that contains the three points: $A = (2, -5, 8)$, $B = (-4, 1, 3)$, and  $C = (1, -2, 3)$.SolutionLet’s first write down the components that make up $\overrightarrow{AB}$ and $\overrightarrow{AC}$ by subtracting their components as shown below.

\begin{aligned}\boldsymbol{\overrightarrow{AB}}\end{aligned}	\begin{aligned}\overrightarrow{AB} &= B – A \\&= <-4 -2, 1 – -5, 3- 8>\\&= <-6, 6, -5>\end{aligned}
\begin{aligned}\boldsymbol{\overrightarrow{AC}}\end{aligned}	\begin{aligned}\overrightarrow{AC} &= C – A \\&= <1 -2, -2 – -5, 3- 8>\\&= <-1, 3, -5>\end{aligned}

Find the normal vector that perpendicular to the plane by taking the cross-product of $\overrightarrow{AB}$ and $\overrightarrow{AC}$.\begin{aligned}\textbf{n} &= \overrightarrow{AB} \times \overrightarrow{AC} \\&= \begin{vmatrix} \textbf{i} &\textbf{j} &\textbf{k} \\ 2 &3 &4 \\ -1 &1 &2 \end{vmatrix}\\&= [6\left(-5\right)-\left(-5\cdot 3\right)]\textbf{i} + [6\left(-5\right)-\left(-5\cdot 3\right)]\textbf{j} + [-6\cdot 3-6\left(-1\right)]\textbf{k}\\&= -15\textbf{i} – 25\textbf{j} -12\textbf{k}\\&= <-15, -25, -12>\end{aligned}Use the point, $A = (2, -5, 8)$, and the normal vector to write down the equation of the plane. The equation will be in scalar form as shown below.\begin{aligned}(x_o, y_o, z_o) &= (2, -5, 8)\\ <a, b, c> &= <-15, -25, -12>\\\\ a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\\-15(x – 2)  -25(y – -25) + -12(z – 8) &= 0\\-15(x – 2) – 25(y + 25) – 12(z – 8) &= 0\end{aligned}Find the other form of this equation by isolating all the variables on the left-hand side of the equation.\begin{aligned}-15(x -2) – 25(y + 25) – 12(z – 8) &= 0\\-15x + 30 – 25y – 625 -12z +96 &= 0\\-15x – 25y -12z &= -30 +625 – 96\\-15x – 25y -12z&= 499\end{aligned}

Practice Questions

1. Find the vector form of the equation of a plane given that both points, $A = (-5, 2, 8)$ and $B = (2, 3, 3)$, lie on the plane. We also know that the vector, $\textbf{n} = <4, 4, -1>$, is perpendicular to the plane.2. Determine the scalar form of the equation of the plane that contains the point $(-6, 3, 5)$ with a vector, $\textbf{n} = <-1, 3, 4>$, that is perpendicular with the plane.3. Find the equation of the plane that contains the three points: $A = (4, -3, 1)$, $B = (-3, -1, 1)$, and $C = (4, -2, 8)$.

Answer Key

1. $\begin{aligned}<4, 4, -1> \cdot <9, 2, -9> &= 0\\<4, 4, -1>\cdot <2, 3, 3>&=<4, 4, -1>\cdot <-5, 2, 8> \end{aligned}$ 2. $\begin{aligned}-(x + 6) + 3(y +3) + 4(z – 5) &= 0\\-x + 3y + 4z &= 35\end{aligned}$ 3. $\begin{aligned}14(x – 4) + 49(y +3) -7(z – 1) &= 0\\2x + 7y -z &= -12\end{aligned}$