JUMP TO TOPIC
Equation of a Line – Explanation and Examples
The equation of a line is any equation that conveys information about a line’s slope and at least one point that lies on it.
While slope alone is not enough information to uniquely identify a line, the equation of a line is. Knowing these equations makes it easy to plot and compare two or more lines to each other.
Equations of a line use lots of algebra. They also require knowledge of the slope of a line and the coordinate plane. Make sure to refresh these concepts before moving forward.
In this topic, we will cover:
- How to Find the Equation of a Line
- How to Find the Equation of a Line with One Point
- How to Find the Equation of a Line with One Point and Slope
How to Find the Equation of a Line
In order to find an equation that uniquely defines a line, we need two things. Namely, we need the slope of the line and one point.
Note, however, that while each equation uniquely defines a line, each line is not uniquely defined by one equation. This makes sense because there is often more than one way to write mathematical expressions.
In any case, if we have a point and a slope, we can find the equation. If, however, we are instead given two points, we can find the slope as discussed in a previous topic. Therefore, we can find the equation of the line as long as we have either two points or one point and the slope because one leads to the other.
How to Find The Equation of a Line with One Point
Technically speaking, one point is not enough information to find the equation for a line. The image below, for example, shows three lines that pass through the point (1, 2).
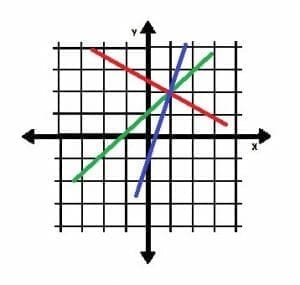
What makes each of these lines different, however, is their slopes. Therefore, if we have the slope of a line (or a way of finding its slope) and one point, we have enough information.
How to Find the Equation of a Line with One Point and Slope
If we know the slope and the coordinates of one point on a line, we can plug this information into the point-slope equation.
Given a slope m and a point (x1, y1), the point-slope equation for the line is y-y1=m(x-x1).
This equation will define the line. Typically, however, it is simplified to solve for y, and the slope is distributed to x and x1. Doing so yields:
y=mx-mx1+y1.
This version of the equation is called the “slope-intercept” form because it is easy to pick out the slope of the line and it’s y-intercept. Remember that a y-intercept is the height of the line when the line crosses the y-axes. It has the coordinates (0, mx1-y1).
More commonly, the slope-intercept form of an equation is written as y=mx+b. Here, b is the y-intercept or mx1-y1.
If the known point of an equation is the y-intercept, then we can skip point-slope form and plug the values into the slope-intercept equation directly. Otherwise, we have to plug the values into point-slope and then solve for y to convert it to slope-intercept form.
Note that if the origin is a know point, then we can simply write the equation of the line as y=mx. This is because, in this case, b=0.
Examples
In this section, we will go through some simple examples to better understand how to find the equation of a line.
Example 1
If a line has a slope of 7⁄6 and a point (12, 4), what is the equation of the line?
Example 1 Solution
We are given a slope and a point, so we can plug these values into the point-slope equation:
y-4=7⁄6(x-12)
y-4=7⁄6x-14
y=7⁄6x+10.
Therefore, the equation of the line is y=7⁄6x+10 in slope-intercept form. From this, we can tell that the line passes through the y-axes at the point (0, 10).
Example 2
A line passes through the points (1, 4) and (2, 6). What is the equation of the line?
Example 2 Solution
In this case, we are not given a slope. We can, however, derive it because we are given two coordinates. Let (1, 4) be (x1, y1), and let (2, 6) be (x2, y2). Then, we have:
m=(4-6)⁄(1-2)=-2⁄-1=2.
Now, we can use this slope with either point in the point slope formula. Using the first gives us:
y-4=2(x-1)
y-4=2x-2
y=2x+2.
Therefore, the equation for the line in slope-intercept form is y=2x+2. We can also see from this that the y-intercept of the line is 2.
Example 3
What is the equation of the line shown in the graph below?
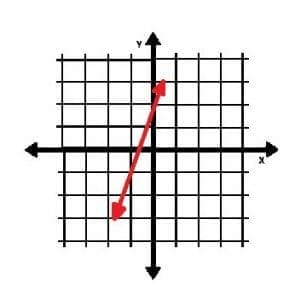
Example 3 Solution
In this case, we are given neither slope nor coordinates. We can find coordinates from the line, though. To make things easier, we can select one of the points as the y-intercept, which is (0, 2). The point (-1, -1) is also on the line. The slope of the line is:
m=(2+1)⁄(0+1)=3.
Since we already have the y-intercept, we can bypass the point-slope equation. The equation for this line is therefore y=3x+2.
Example 4
A line k is perpendicular to the line defined by the equation y=5⁄6x. The line k also passes through the point (10, 1). What is the equation of the line k?
Example 4 Solution
We are not given the slope of k explicitly, but we can calculate it because we know it is perpendicular to the line y=5⁄6x. The slope of that line is 5⁄6, so a perpendicular line has a slope -6⁄5, the opposite reciprocal.
Now we have a point and the slope, so we can plug them into the point-slope equation:
y-1=-6⁄5(x-10)
y-1=-6⁄5x+12
y=-6⁄5x+13.
Therefore, the equation y=-6⁄5x+13 defines the line k. This line also has a y-intercept of 13.
Example 5
The line k is parallel to the line l shown below.
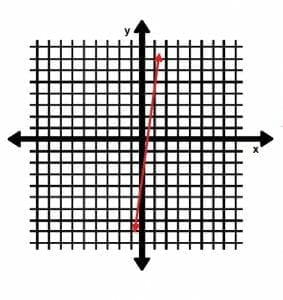
The line k also passes through the point (5, 24). What is the y-intercept of k?
Example 5 Solution
We know one point for k, but we do not know its slope. Since its slope is parallel to the line l, however, we can determine it by finding l’s slope.
We can pick any two points from l to do this. It is clear from the graph that the line l crosses the y-axes at the point (0, -3). It also passes through the point (1, 5). The slope is therefore:
m=(-3-5)⁄(0-1)=-8⁄-1=8.
Consequently, k has a slope of 8 as well. We can now employ the point-slope formula:
y-24=8(x-5)
y-24=8x-40
y-8x-16
