- Home
- >
- Even and Odd Functions – Properties & Examples
JUMP TO TOPIC
Even and Odd Functions – Properties & Examples
 When working with functions and graphs, you’ll encounter instances where functions are described as even or odd. If you’re curious about even and odd functions, you just found the right article. Let’s begin with their definition:
When working with functions and graphs, you’ll encounter instances where functions are described as even or odd. If you’re curious about even and odd functions, you just found the right article. Let’s begin with their definition:
Even and odd functions are special functions that exhibit special symmetry about the y-axis and origin, respectively.
Why do we need to know whether a function is odd or even? Knowing this important property of a function can help us:
- Know the behavior of the function’s graph.
- Save our time in graphing functions and apply the properties of odd and even functions instead.
- Predict the nature of two functions’ product and sum.
Seeing that this can help us work on the next topics much faster, we should make sure we cover all aspects of odd and even functions. Let’s start with the latter!
What is an even function?
This section will study even function thoroughly, including its definition, properties, and graph. Below are some functions that are widely known as even functions:
- Absolute value functions
- Cosine functions
- Most functions with an even-numbered degree
We will be able to understand why the functions above are even functions after the next two sections. So, how do we know if a given function is even?
Even function definition
Even functions are functions that return the same expression for both x and -x. This means that if f(x) is an even function when f(-x) = f(x). An even function’s table of values will also have symmetric values. The quadratic function, f(x) = x2, is an even function. Observe how it meets the definition of even functions:
f(-x) = (-x)2
= x2
We can see that [x, f(x)] → [-x, f(x)], showing how f(x) satisfies the definition of an even function. Now, take a look at its table of values.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
As can be seen, x and its negative counterpart’s value will have the same values making each half of the table identical.
Even function graph and understanding its symmetry
Since we already have the table of values for f(x) = x2, why don’t we use these to graph the function?
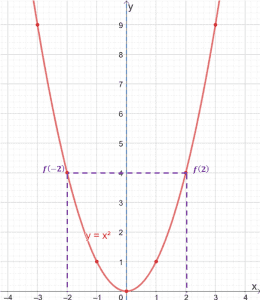
The graph above shows us how the quadratic function is symmetric about the y-axis as well. What does this mean for us moving forward?
You can graph half of any even functions, then reflect it over the y-axis. This saves us a lot of time since we only need the ordered pairs to graph either the left or the right side of the even function.
Why don’t we give it a try by plotting half of the absolute value function, f(x) = |x|, first?
| x | 0 | 1 | 2 | 3 | 4 |
| f(x) | 0 | 1 | 4 | 9 | 16 |
Once we’ve plotted the right side of f(x) = |x|, let’s reflect it about the axis to show the function’s completed graph.
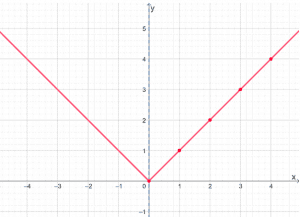
This graphing technique will save you time, especially when working with more complicated expressions. Don’t forget, though, to double-check and make sure that the function is even.
What is an odd function?
Now that we’ve learned about even functions, it’s time to refresh our knowledge on odd functions. These are some of the well-known odd functions that you may have already encountered:
- Reciprocal functions
- Sine and tangent functions
- Most functions with an odd-numbered degree
We will understand why the functions mentioned above are odd functions after the next two sections. So, what makes odd functions special?
Odd function definition
Odd functions are functions that return its negative inverse when x is replaced with –x. This means that f(x) is an odd function when f(-x) = -f(x). Let’s try to observe f(x) = x3, an odd function, and see how this affects its table of values.
f(-x) = (-x)3
= – x3
This confirms that [x, f(x)] → [-x, -f(x)]. The table of values for f(x) = x3 is as shown below. Notice some patterns?
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | -27 | -8 | -1 | 0 | 1 | 8 | 27 |
See how f(1) = -f(1)? This pattern is consistent for the rest of the values. The left side of the table shows the negative values of its counterpart from the right side.
Odd function graph and understanding its symmetry
We can also observe how odd functions behave on the xy-coordinate by graphing f(x) = x3. Use the table of values shown in the previous section to plot the points that will connect the curve of f(x) = x3.
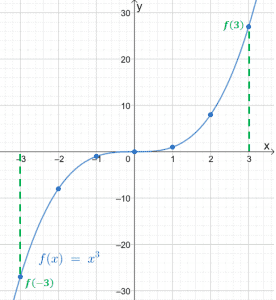
This graph clearly shows us how odd functions are symmetric about the origin. We can use this property as well to shorten the time we need to graph odd functions. Want to see an example? Let’s try graphing f(x) = 1/x.
| x | 1/4 | 1/2 | 1 | 2 | 4 |
| f(x) | 4 | 2 | 1 | 1/2 | 1/4 |
After plotting the upper part of the reciprocal function, we can reflect it on the origin to complete the graph. Check out the dashed line as a guide on how we reflect graphs about the origin.
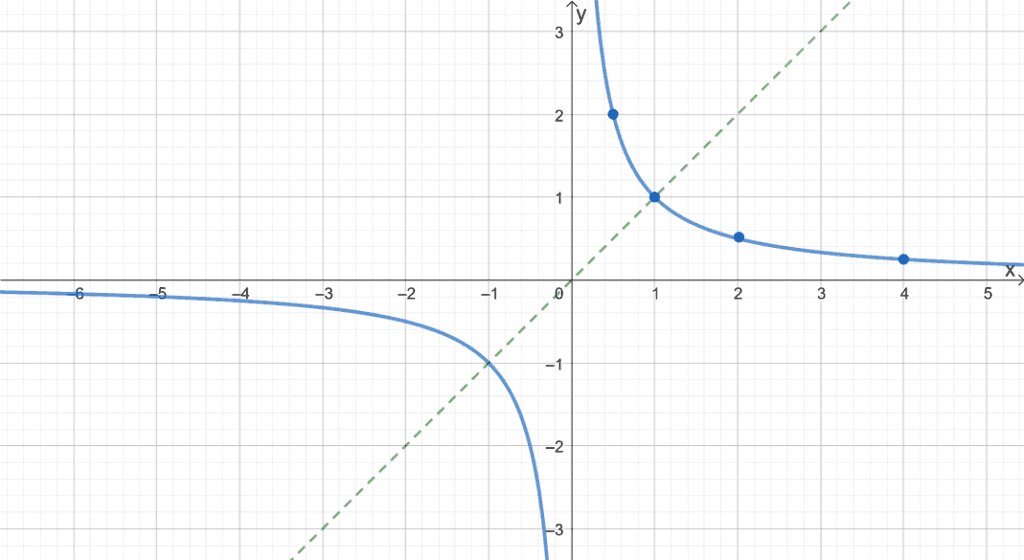
With more practice and examples, you’ll definitely be able to graph even and odd functions easily. Let’s always remember to check whether the graph is odd or even before applying the appropriate technique.
What are some properties of even and odd functions?
Now that we’ve learned about odd and even functions, what are other properties that we can observe with these types of functions?
- The sum, difference, quotient, or product of two even functions will be even. The same goes for odd functions.
- Example: f(x) = sin x and g(x) = tan x are odd, so h(x) = sin x + tan x will also be odd.
- The composition of two even functions will be even. The same rule applies for odd functions.
- Example: f(x) = x2 and g(x) = cos x are even, so f(g(x)) = (cos x)2 will also be odd.
How to tell if a function is even or odd?
What if we’re given a function and don’t know whether it is either odd or even? That won’t be a problem! Let’s use what we have learned so far to determine whether a function is odd or even.
When given the function: observe what happens when we replace x with –x.
- When you plug in –x into f(x), did the function remain the same? If so, f(x) is even.
- When you plug in –x into f(x), did the sign of function’s coefficient change? If so, f(x) is odd.
When given the graph: determine whether the graph is symmetric about the origin or y-axis.
- If the graph is symmetric about the y-axis, the function is even. How do we do this?
- Imagine folding the graph vertically and see if the two graphs would lie along with each other.
- You can also spot multiple points and see if x and –x share the same coordinate.
- If the graph is symmetric about the origin, the function is odd. How do we do this?
- Imagine folding the graph diagonally (check both directions) and see if the two graphs would lie along with each other.
- You can also spot for multiple points and see if x and –x share the y-
Are there functions that are neither odd nor even?
Should all functions be either odd or even? No. There are instances where a function neither meets the definition of even and odd functions. The function f(x) = (x + 1)2 is an example of a function that is neither odd nor even.
Let’s go ahead and observe the expression for f(-x):
f(x) = (x + 1)2
f(-x) = (-x + 1)2
= (1 – x)2
= 1 – 2x + x2
Compare this expression with the expanded form of f(x) and –f(x).
| Test for Odd Function: f(-x) = -f(x) | Test for Even Function: f(-x) = f(x) |
-f(x) = -(x + 1)2 =-(x2 + 2x + 1) =-x2 – 2x – 1 f(-x) ≠ -f(x) | f(x) = (x + 1)2 =x2 + 2x + 1 f(-x) ≠ f(x) |
This shows that a function such as f(x) = (x + 1)2 can neither be odd nor even.
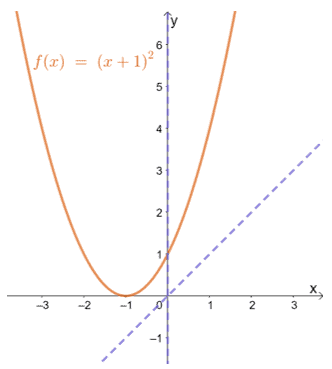
If you look at the f(x) graph, you can see that it is not symmetric about the origin or the y-axis. This further confirms that the function is neither odd nor even.
Just like that, we’ve covered all essential topics on even and odd functions. With all the properties, rules, and definitions that we just learned, we are now ready to work on more examples to understand even further and odd functions.
Example 1
Fill in the blank with either odd or even to make the following statements true.
- The functions f(x) and g(x) are both even functions, so their sum would also be an _________ function.
- The composition of f(x) and g(x) returns an odd function, so both f(x) and g(x) are _________ functions.
- The absolute value of an odd function is an _____________ function.
Solution
- The sum of two even functions will also be even.
- The composition of two odd functions will also be odd.
- Let’s say f(x) is odd, so f(-x) is equal to -f(x). Taking the absolute value of this function returns f(x) back. This means that the function is even.
Example 2
Determine whether f(x), g(x), and h(x) are either even or odd functions using their tables of values shown below.
a.
| x | -4 | -2 | 0 | 2 | 4 |
| f(x) | 17 | 5 | 1 | 5 | 17 |
b.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | 18 | 4 | 1 | 4 | 18 |
c.
| x | -4 | -2 | -1/2 | 0 | 1/2 | 2 | 4 |
| h(x) | -64 | -8 | -1/8 | 0 | 1/8 | 8 | 64 |
Solution
Observe how the values on each half of the table look like. Are the corresponding values equal? Are the values on the left-hand side the negative value of the ones on the right?
- We can see that table of values for f(x) show identical values for f(-x) and f(x), the function is even.
- We can say the same for the values shown for g(x), so the function is even.
- The left-hand side of the tables are the negative values of the one on the side, so the function is odd.
Example 3
Identify whether the following functions are even, odd, or neither.
- f(x) = x2 – 1
- g(x) = |x -1|
- h(x) = -3x5
Solution
Replace x with -x and check the function’s expression. If f(-x) returns the same function, we can conclude that the function is even. If it returns the same function, but with its coefficients having opposite signs, it is odd.
- Let’s check the first function, f(x) = x2 – 1.
f(-x) = (-x)2 – 1
= x2 – 1
Since f(-x) returns the same expression for f(x), the function is even.
Using the same process for b and c, we have the following results.
2.
g(-x) = |x – 1|
= |-x – 1|
= |-(x + 1)|
=|x + 1|
Since g(-x) is neither equal to g(x) or -g(x), g(x) is neither odd nor even.
3.
h(-x) = -3(-x)5
= -3(-x5)
= 3x5
=-(-3x5)
We can see that h(-x) = -h(x), so h(x) is an odd function.
Example 4
Determine whether the following functions are even, odd, or neither by inspecting the following functions’ graphs.
a.
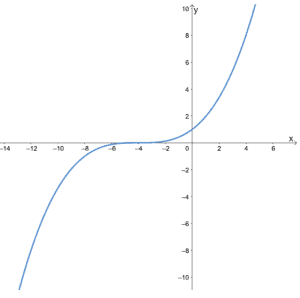
b.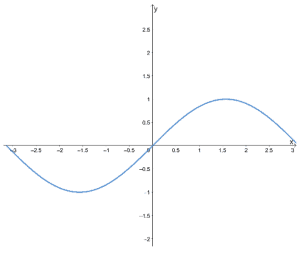
c.
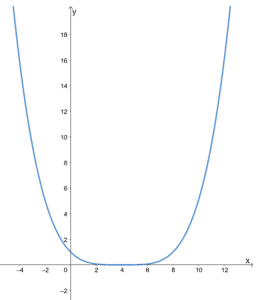
Solution
When given a graph, we can identify odd and even functions based on the graph’s symmetry.
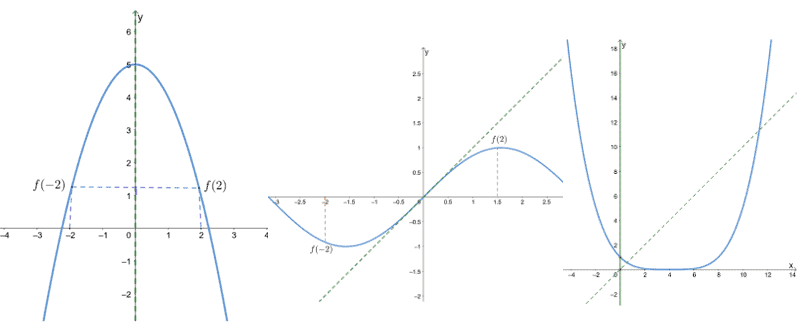
- The first graph shows that it is symmetric about the y-axis, so it is an even function.
- The second graph shows that it is symmetric about the origin, so it is an odd function.
- Since the third graph is neither symmetric about the origin or the y-axis, it is neither odd nor even.
Example 5
Complete the table below by using the property of the functions.
- The function f(x) is odd.
| x | -1 | -1/2 | -1/4 | 1/2 | 1/4 | 1 |
| f(x) | -2 | -4 | -8 |
2. The function f(x) is even.
| x | -3 | -1 | 0 | 1 | 3 |
| f(x) | -6 | -5 | -3 |
Solution
- Since the function is odd, we fill in the unfilled values with the negative inverse of -2, -4, and -8. Hence, we have 2, 4, and 8.
- Since the function is even, we fill in the unfilled values that will be the same as the f(1) and f(3). Hence, we have 3 and 1.
Example 6
Use the table of values shown below and the fact that f(x) is even to graph f(x).
| x | -3 | -2 | -1 | 0 |
| f(x) | 0 | -2 | -4 | -6 |
Solution
Let’s go ahead and plot the points first. Connect them to graph a part of f(x).
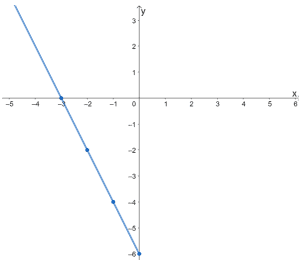
Remember that f(x) is an even function. Its graph would be symmetric about the y-axis. This means that for us to complete the graph of f(x), we reflect the graph about the y-axis.
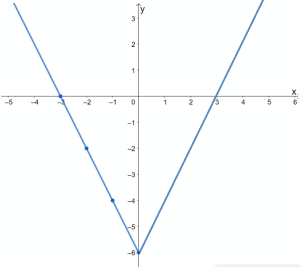
The graph above shows the complete graph of f(x). You can also confirm this by visualizing the remaining half of the function’s graph by “folding” the graph along the y-axis.
This shows that understanding the properties of odd and even functions can save us time in solving problems and graphing functions.
Practice Questions
![]()
Open Problems
1. Complete the table below by using the given property of the functions.
a. The function $f(x)$ is odd.
| $x$ | $-1$ | $-1/3$ | $-1/6$ | $1/3$ | $1/6$ | $1$ |
| $f(x)$ | $-1$ | $-3$ | $-6$ |
b. The function $g(x)$ is even.
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $g(x)$ | $18$ | $6$ | $-6$ |
2. Use the table of values shown below and the fact that $f(x)$ is odd to graph its curve.
| $x$ | $-6$ | $-4$ | $-2$ | $0$ |
| $f(x)$ | $-3$ | $-2$ | $-1$ | $0$ |
Open Problem Solutions
1.
a. The function $f(x)$ is odd.
| $x$ | $-1$ | $-1/3$ | $-1/6$ | $1/3$ | $1/6$ | $1$ |
| $f(x)$ | $-1$ | $-3$ | $-6$ | $1$ | $3$ | $6$ |
b. The function $g(x)$ is even.
| $x$ | $-4$ | $-2$ | $0$ | $2$ | $4$ |
| $g(x)$ | $18$ | $6$ | $-6$ | $6$ | $18$ |
2.
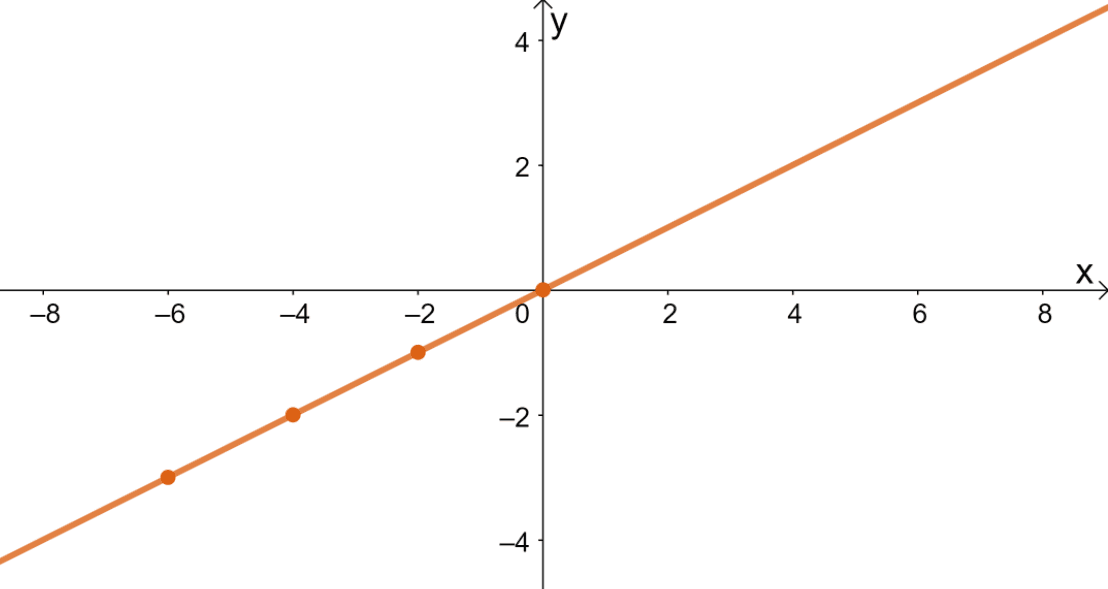
Images/mathematical drawings are created with GeoGebra.
