Rules of Exponents – Laws & Examples
The history of exponents or powers is pretty old. In 9th century, a Persian Mathematician Muhammad Musa introduced square of a number. Later in 15th century, they introduced a cube of a number. The symbols to represent these indices are different, but the method of calculation was same.
The term ‘exponent’ was first used in 1544 and the term ‘indices’ was first used in 1696. In the 17th century, the exponential notation got maturity and mathematicians all over the world started using them in the problems.
Exponents have many applications, especially in population growth, chemical reactions, and many other fields of physics and biology. One of the recent examples of exponents is the trend found for the spread of the pandemic Novel Coronavirus (COVID-19), which shows exponential growth in the number of infected persons.
What are Exponents?
Exponents are powers or indices. They are widely used in algebraic problems, and for this reason, its important to learn them so as to make studying of algebra easy. First of all, lets start by studying the parts of an exponential number.
An exponential expression consists of two parts, namely the base, denoted as b and the exponent, denoted as n. The general form of an exponential expression is b n. For example, 3 x 3 x 3 x 3 can be written in exponential form as 34 where 3 is the base and 4 is the exponent.
The base is the first component of an exponential number. The base is basically a number or variable that is repeatedly multiplied by itself. Whereas the exponent is the second element which is positioned at the upper right corner of the base. The exponent specifies the number of times the base will be multiplied by itself.
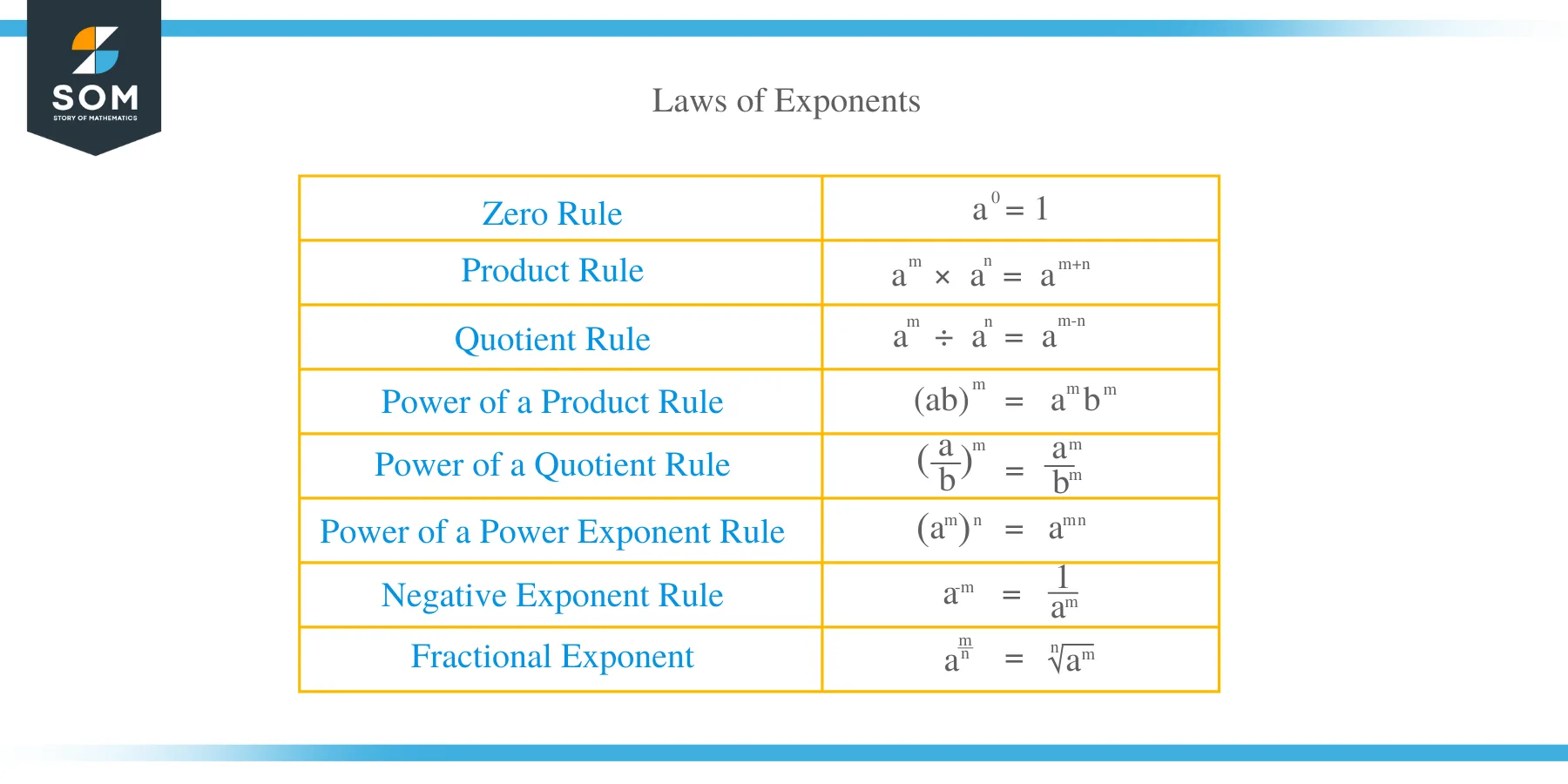
Laws of Exponents
The following are the rule or laws of exponents:
- Multiplication of powers with a common base.
The law implies that if the exponents with same bases are multiplied, then exponents are added together. In general:
a ᵐ × a ⁿ = a m +n and (a/b) ᵐ × (a/b) ⁿ = (a/b) m + n
Examples
1. 2³ × 2² = (2 × 2 × 2) × (2 × 2) = 2 3 + 2 = 2 ⁵
2. 5 ³ × 5 ⁶
= (5 × 5 × 5) × (5 × 5 × 5 × 5 × 5 × 5)
= 5 3 + 6
= 5 ⁹
3. (-7)10× (-7) ¹²
= [(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7)] × [( -7) × (-7) × (-7) ×
(-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7) × (-7)]
= (-7) 10 + 12
= (-7) ²²
4. (4/9) 3 x (4/9) 2
= (4/9)3 + 2
= (4/9) 5
- Dividing exponents with the same base
In the division of exponential numbers with same base, we need to do subtraction of exponents. The general forms of this law are: (a) m ÷ (a) n = a m – n and (a/b) m ÷ (a/b) n = (a/b) m – n
Examples
1. 10 ⁵ ÷ 10 ³ = (10) 5/ (10) 3
= (10 x 10 x 10 x 10 x 10)/ (10 x 10 x 10)
= 10 5 – 3
= 10 2
2. (7/2) 8 ÷ (7/2) 5
= (7/2)8 – 5
= (7/2) ³
- The law of power of a power
This law implies that, we need to multiply the powers incase an exponential number is raised to another power. The general law is:
(a m) n = a m x n
Examples
1. (3 ²) ⁴ = 3 2 x 4 = 3 8
2. {(2/3)2} 3 = (2/3) 2 x 3 = (2/3) 6
- The law of multiplication of powers with different bases but same exponents.
The general form of the rule is: (a) m x (b) m = (ab) m
Examples
1. 4³ × 2³
= (4 × 4 × 4) × (2 × 2 × 2)
= (4 × 2) × (4 × 2) × (4 × 2)
= 8 × 8 × 8
= 8 ³
2. 2³ × a³
= (2 × 2 × 2) × (a × a × a)
= (2 × a) × (2 × a) × (2 × a)
= (2 × a) ³
= (2a) ³
- The law of negative exponents
When an exponent is negative, we change it to positive by writing 1 in the numerator and the positive exponent in the denominator. The general forms of this law are: a -m = 1/a m a and (a/b) -n = (b/a) n
Examples
1. 2 -2 = 1/22 = 1/4
2. (2/3) -2 = (3/2) 2
- The law of exponent zero
If the exponent is zero then you get 1 as the result. The general form is: a 0 = 1 and (a/b) 0 = 1
Examples
1. (-3) 0 = 1
2. (2/3) 0 = 1
- Fractional exponents
In the fractional exponent, the general formula is: a 1/n = n √a where a is the base and 1/n is the exponent. See the examples below.
Examples
1. 4 1/1 = 4
2. 4 1/2 = √4 = 2 (squire root of 4)
3. 9 1/3 = 3 √9 =3 (cube root of 9)
