MUHAMMAD IBN MUSA AL-KHWARIZMI: The Father Of Algebra. Muslim Mathematician

Biography

Muhammad Al-Khwarizmi (c.780-850 CE)

One of the first Directors of the House of Wisdom in Bagdad in the early 9th Century was an outstanding Persian mathematician called Muhammad Al-Khwarizmi. He oversaw the translation of the major Greek and Indian mathematical and astronomy works (including those of Brahmagupta) into Arabic, and produced original work which had a lasting influence on the advance of Muslim and (after his works spread to Europe through Latin translations in the 12th Century) later European mathematics.

The word “algorithm” is derived from the Latinization of his name, and the word “algebra” is derived from the Latinization of “al-jabr“, part of the title of his most famous book, in which he introduced the fundamental algebraic methods and techniques for solving equations.

Perhaps his most important contribution to mathematics was his strong advocacy of the Hindu numerical system, which Al-Khwarizmi recognized as having the power and efficiency needed to revolutionize Islamic and Western mathematics. The Hindu numerals 1 – 9 and 0 – which have since become known as Hindu-Arabic numerals – were soon adopted by the entire Islamic world. Later, with translations of Al-Khwarizmi’s work into Latin by Adelard of Bath and others in the 12th Century, and with the influence of Fibonacci’s “Liber Abaci” they would be adopted throughout Europe as well.

Who created algebra – The Father Of Algebra

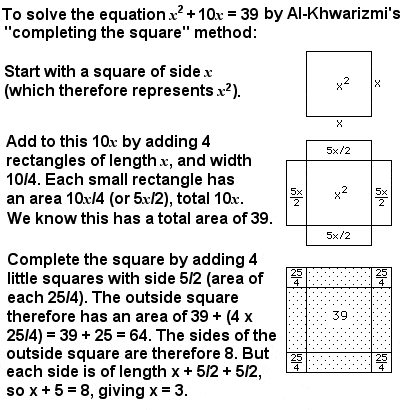An example of Al-Khwarizmi’s “completing the square” method for solving quadratic equations

Al-Khwarizmi’s other important contribution was algebra, a word derived from the title of a mathematical text he published in about 830 called “Al-Kitab al-mukhtasar fi hisab al-jabr wa’l-muqabala” (“The Compendious Book on Calculation by Completion and Balancing”). Al-Khwarizmi wanted to go from the specific problems considered by the Indians and Chinese to a more general way of analyzing problems, and in doing so he created an abstract mathematical language which is used across the world today.

His book is considered the foundational text of modern algebra, although he did not employ the kind of algebraic notation used today (he used words to explain the problem, and diagrams to solve it). But the book provided an exhaustive account of solving polynomial equations up to the second degree, and introduced for the first time the fundamental algebraic methods of “reduction” (rewriting an expression in a simpler form), “completion” (moving a negative quantity from one side of the equation to the other side and changing its sign) and “balancing” (subtraction of the same quantity from both sides of an equation, and the cancellation of like terms on opposite sides).

In particular, Al-Khwarizmi developed a formula for systematically solving quadratic equations (equations involving unknown numbers to the power of 2, or x²) by using the methods of completion and balancing to reduce any equation to one of six standard forms, which were then solvable. He described the standard forms in terms of “squares” (what would today be “x²“), “roots” (what would today be “x“) and “numbers” (regular constants, like 42), and identified the six types as: squares equal roots (ax² = bx), squares equal number (ax² = c), roots equal number (bx = c), squares and roots equal number (ax² + bx = c), squares and number equal roots (ax² + c = bx), and roots and number equal squares (bx + c = ax²).

Al-Khwarizmi is usually credited with the development of lattice (or sieve) multiplication method of multiplying large numbers, a method algorithmically equivalent to long multiplication. His lattice method was later introduced into Europe by Fibonacci.

In addition to his work in mathematics, Al-Khwarizmi made important contributions to astronomy, also largely based on methods from India, and he developed the first quadrant (an instrument used to determine time by observations of the Sun or stars), the second most widely used astronomical instrument during the Middle Ages after the astrolabe. He also produced a revised and completed version of Ptolemy’s “Geography”, consisting of a list of 2,402 coordinates of cities throughout the known world.