BRAHMAGUPTA: MATHEMATICIAN AND ASTRONOMER
Biography
 |
Brahmagupta (598–668 CE) |
The great 7th Century Indian mathematician and astronomer Brahmagupta wrote some important works on both mathematics and astronomy. He was from the state of Rajasthan of northwest India (he is often referred to as Bhillamalacarya, the teacher from Bhillamala), and later became the head of the astronomical observatory at Ujjain in central India. Most of his works are composed in elliptic verse, a common practice in Indian mathematics at the time, and consequently have something of a poetic ring to them.
It seems likely that Brahmagupta’s works, especially his most famous text, the “Brahmasphutasiddhanta”, were brought by the 8th Century Abbasid caliph Al-Mansur to his newly founded centre of learning at Baghdad on the banks of the Tigris, providing an important link between Indian mathematics and astronomy and the nascent upsurge in science and mathematics in the Islamic world.
In his work on arithmetic, Brahmagupta explained how to find the cube and cube-root of an integer and gave rules facilitating the computation of squares and square roots. He also gave rules for dealing with five types of combinations of fractions. He gave the sum of the squares of the first n natural numbers as n(n + 1)(2n + 1)⁄ 6 and the sum of the cubes of the first n natural numbers as (n(n + 1)⁄2)².
Brahmasphutasiddhanta – Treat Zero as a Number
 |
Brahmagupta’s rules for dealing with zero and negative numbers |
Brahmagupta’s genius, though, came in his treatment of the concept of (then relatively new) the number zero. Although often also attributed to the 7th Century Indian mathematician Bhaskara I, his “Brahmasphutasiddhanta” is probably the earliest known text to treat zero as a number in its own right, rather than as simply a placeholder digit as was done by the Babylonians, or as a symbol for a lack of quantity as was done by the Greeks and Romans.
Brahmagupta established the basic mathematical rules for dealing with zero (1 + 0 = 1; 1 – 0 = 1; and 1 x 0 = 0), although his understanding of division by zero was incomplete (he thought that 1 ÷ 0 = 0). Almost 500 years later, in the 12th Century, another Indian mathematician, Bhaskara II, showed that the answer should be infinity, not zero (on the grounds that 1 can be divided into an infinite number of pieces of size zero), an answer that was considered correct for centuries. However, this logic does not explain why 2 ÷ 0, 7 ÷ 0, etc, should also be zero – the modern view is that a number divided by zero is actually “undefined” (i.e. it doesn’t make sense).
Brahmagupta’s view of numbers as abstract entities, rather than just for counting and measuring, allowed him to make yet another huge conceptual leap which would have profound consequence for future mathematics. Previously, the sum 3 – 4, for example, was considered to be either meaningless or, at best, just zero. Brahmagupta, however, realized that there could be such a thing as a negative number, which he referred to as “debt” as a opposed to “property”. He expounded on the rules for dealing with negative numbers (e.g. a negative times a negative is a positive, a negative times a positive is a negative, etc).
Furthermore, he pointed out, quadratic equations (of the type x2 + 2 = 11, for example) could in theory have two possible solutions, one of which could be negative, because 32 = 9 and -32 = 9. In addition to his work on solutions to general linear equations and quadratic equations, Brahmagupta went yet further by considering systems of simultaneous equations (set of equations containing multiple variables), and solving quadratic equations with two unknowns, something which was not even considered in the West until a thousand years later, when Fermat was considering similar problems in 1657.
Brahmagupta’s Theorem on cyclic quadrilaterals
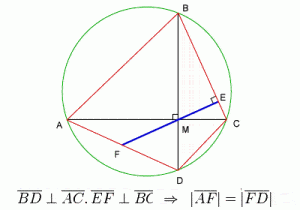 |
Brahmagupta’s Theorem on cyclic quadrilaterals |
Brahmagupta even attempted to write down these rather abstract concepts, using the initials of the names of colours to represent unknowns in his equations, one of the earliest intimations of what we now know as algebra.
Brahmagupta dedicated a substantial portion of his work to geometry and trigonometry. He established √10 (3.162277) as a good practical approximation for π (3.141593), and gave a formula, now known as Brahmagupta’s Formula, for the area of a cyclic quadrilateral, as well as a celebrated theorem on the diagonals of a cyclic quadrilateral, usually referred to as Brahmagupta’s Theorem.
<< Back to Indian Mathematics | Forward to Madhava >> |
