ISLAMIC MATHEMATICS
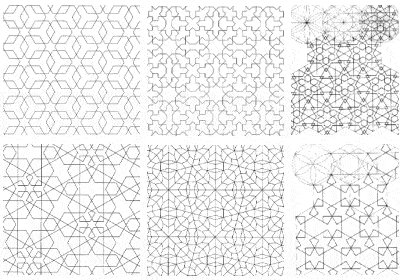 |
Some examples of the complex symmetries used in Islamic temple decoration |
The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberia and parts of India from the 8th Century onwards made significant contributions towards mathematics. They were able to draw on and fuse together the mathematical developments of both Greece and India.
One consequence of the Islamic prohibition on depicting the human form was the extensive use of complex geometric patterns to decorate their buildings, raising mathematics to the form of an art. In fact, over time, Muslim artists discovered all the different forms of symmetry that can be depicted on a 2-dimensional surface.
The Qu’ran itself encouraged the accumulation of knowledge, and a Golden Age of Islamic science and mathematics flourished throughout the medieval period from the 9th to 15th Centuries. The House of Wisdom was set up in Baghdad around 810, and work started almost immediately on translating the major Greek and Indian mathematical and astronomy works into Arabic.
The outstanding Persian mathematician Muhammad Al-Khwarizmi was an early Director of the House of Wisdom in the 9th Century, and one of the greatest of early Muslim mathematicians. Perhaps Al-Khwarizmi’s most important contribution to mathematics was his strong advocacy of the Hindu numerical system (1 – 9 and 0), which he recognized as having the power and efficiency needed to revolutionize Islamic (and, later, Western) mathematics, and which was soon adopted by the entire Islamic world, and later by Europe as well.
Al-Khwarizmi‘s other important contribution was algebra, and he introduced the fundamental algebraic methods of “reduction” and “balancing” and provided an exhaustive account of solving polynomial equations up to the second degree. In this way, he helped create the powerful abstract mathematical language still used across the world today, and allowed a much more general way of analyzing problems other than just the specific problems previously considered by the Indians and Chinese.
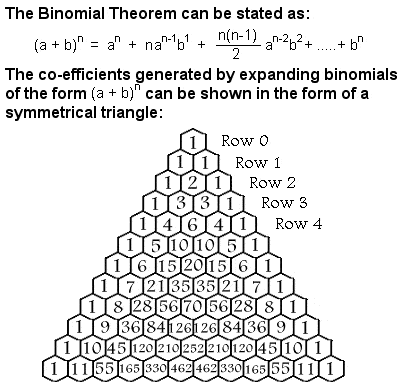 |
Binomial Theorem |
The 10th Century Persian mathematician Muhammad Al-Karaji worked to extend algebra still further, freeing it from its geometrical heritage, and introduced the theory of algebraic calculus. Al-Karaji was the first to use the method of proof by mathematical induction to prove his results, by proving that the first statement in an infinite sequence of statements is true, and then proving that, if any one statement in the sequence is true, then so is the next one.
Binomial Theorem
Among other things, Al-Karaji used mathematical induction to prove the binomial theorem. A binomial is a simple type of algebraic expression which has just two terms which are operated on only by addition, subtraction, multiplication and positive whole-number exponents, such as (x + y)2. The co-efficients needed when a binomial is expanded form a symmetrical triangle, usually referred to as Pascal’s Triangle after the 17th Century French mathematician Blaise Pascal, although many other mathematicians had studied it centuries before him in India, Persia, China and Italy, including Al-Karaji.
Some hundred years after Al-Karaji, Omar Khayyam (perhaps better known as a poet and the writer of the “Rubaiyat”, but an important mathematician and astronomer in his own right) generalized Indian methods for extracting square and cube roots to include fourth, fifth and higher roots in the early 12th Century. He carried out a systematic analysis of cubic problems, revealing there were actually several different sorts of cubic equations. Although he did in fact succeed in solving cubic equations, and although he is usually credited with identifying the foundations of algebraic geometry, he was held back from further advances by his inability to separate the algebra from the geometry, and a purely algebraic method for the solution of cubic equations had to wait another 500 years and the Italian mathematicians del Ferro and Tartaglia.
Spherical Trigonometry
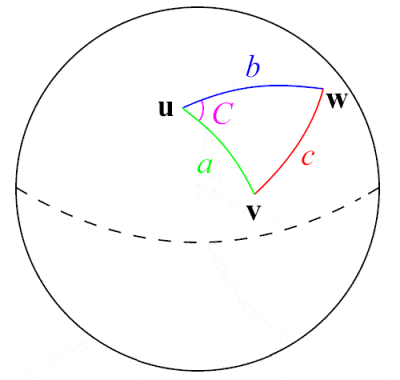 |
Al-Tusi was a pioneer in the field of spherical trigonometry |
The 13th Century Persian astronomer, scientist and mathematician Nasir Al-Din Al-Tusi was perhaps the first to treat trigonometry as a separate mathematical discipline, distinct from astronomy. Building on earlier work by Greek mathematicians such as Menelaus of Alexandria and Indian work on the sine function, he gave the first extensive exposition of spherical trigonometry, including listing the six distinct cases of a right triangle in spherical trigonometry. One of his major mathematical contributions was the formulation of the famous law of sines for plane triangles, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), although the sine law for spherical triangles had been discovered earlier by the 10th Century Persians Abul Wafa Buzjani and Abu Nasr Mansur.
Other medieval Muslim mathematicians worthy of note include:
- the 9th Century Arab Thabit ibn Qurra, who developed a general formula by which amicable numbers could be derived, re-discovered much later by both Fermat and Descartes(amicable numbers are pairs of numbers for which the sum of the divisors of one number equals the other number, e.g. the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, of which the sum is 284; and the proper divisors of 284 are 1, 2, 4, 71, and 142, of which the sum is 220);
- the 10th Century Arab mathematician Abul Hasan al-Uqlidisi, who wrote the earliest surviving text showing the positional use of Arabic numerals, and particularly the use of decimals instead of fractions (e.g. 7.375 insead of 73⁄8);
- the 10th Century Arab geometer Ibrahim ibn Sinan, who continued Archimedes‘ investigations of areas and volumes, as well as on tangents of a circle;
- the 11th Century Persian Ibn al-Haytham (also known as Alhazen), who, in addition to his groundbreaking work on optics and physics, established the beginnings of the link between algebra and geometry, and devised what is now known as “Alhazen’s problem” (he was the first mathematician to derive the formula for the sum of the fourth powers, using a method that is readily generalizable); and
- the 13th Century Persian Kamal al-Din al-Farisi, who applied the theory of conic sections to solve optical problems, as well as pursuing work in number theory such as on amicable numbers, factorization and combinatorial methods;
- the 13th Century Moroccan Ibn al-Banna al-Marrakushi, whose works included topics such as computing square roots and the theory of continued fractions, as well as the discovery of the first new pair of amicable numbers since ancient times (17,296 and 18,416, later re-discovered by Fermat) and the the first use of algebraic notation since Brahmagupta.
With the stifling influence of the Turkish Ottoman Empire from the 14th or 15th Century onwards, Islamic mathematics stagnated, and further developments moved to Europe.
<< Back to Madhava | Forward to Al-Khwarizmi >> |
