16TH CENTURY MATHEMATICS
 |
The supermagic square shown in Albrecht Dürer’s engraving “Melencolia I” |
The cultural, intellectual and artistic movement of the Renaissance, which saw a resurgence of learning based on classical sources, began in Italy around the 14th Century, and gradually spread across most of Europe over the next two centuries. Science and art were still very much interconnected and intermingled at this time, as exemplified by the work of artist/scientists such as Leonardo da Vinci, and it is no surprise that, just as in art, revolutionary work in the fields of philosophy and science was soon taking place.
The Supermagic Square
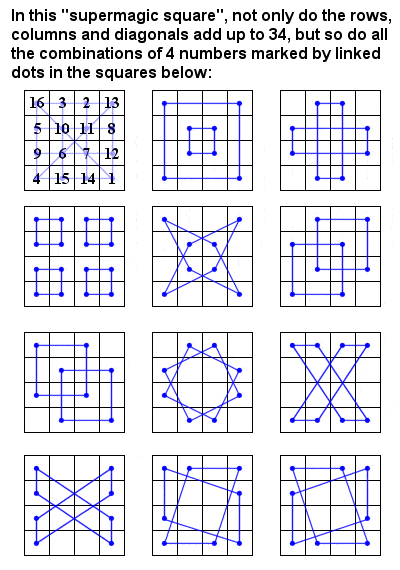
It is a tribute to the respect in which mathematics was held in Renaissance Europe that the famed German artist Albrecht Dürer included an order-4 magic square in his engraving “Melencolia I“. In fact, it is a so-called “super magic square” with many more lines of addition symmetry than a regular 4 x 4 magic square (see image at right). The year of the work, 1514, is shown in the two bottom central squares.
An important figure in the late 15th and early 16th Centuries is an Italian Franciscan friar called Luca Pacioli, who published a book on arithmetic, geometry and book-keeping at the end of the 15th Century which became quite popular for the mathematical puzzles it contained. It also introduced symbols for plus and minus for the first time in a printed book (although this is also sometimes attributed to Giel Vander Hoecke, Johannes Widmann and others), symbols that were to become standard notation. Pacioli also investigated the Golden Ratio of 1 : 1.618… (see the section on Fibonacci) in his 1509 book “The Divine Proportion”, concluding that the number was a message from God and a source of secret knowledge about the inner beauty of things.
 |
Basic mathematical notation, with dates of first use |
During the 16th and early 17th Century, the equals, multiplication, division, radical (root), decimal and inequality symbols were gradually introduced and standardized. The use of decimal fractions and decimal arithmetic is usually attributed to the Flemish mathematician Simon Stevin the late 16th Century, although the decimal point notation was not popularized until early in the 17th Century. Stevin was ahead of his time in enjoining that all types of numbers, whether fractions, negatives, real numbers or surds (such as √2) should be treated equally as numbers in their own right.
In the Renaissance Italy of the early 16th Century, Bologna University in particular was famed for its intense public mathematics competitions. It was in just such a competion that the unlikely figure of the young, self-taught Niccolò Fontana Tartaglia revealed to the world the formula for solving first one type, and later all types, of cubic equations (equations with terms including x3), an achievement hitherto considered impossible and which had stumped the best mathematicians of China, India and the Islamic world.
Building on Tartaglia’s work, another young Italian, Lodovico Ferrari, soon devised a similar method to solve quartic equations (equations with terms including x4) and both solutions were published by Gerolamo Cardano. Despite a decade-long fight over the publication, Tartaglia, Cardano and Ferrari between them demonstrated the first uses of what are now known as complex numbers, combinations of real and imaginary numbers (although it fell to another Bologna resident, Rafael Bombelli, to explain what imaginary numbers really were and how they could be used). Tartaglia went on to produce other important (although largely ignored) formulas and methods, and Cardano published perhaps the first systematic treatment of probability.
With Hindu-Arabic numerals, standardized notation and the new language of algebra at their disposal, the stage was set for the European mathematical revolution of the 17th Century.
<< Back to Fibonacci | Forward to Tartaglia, Cardano & Ferrari >> |
