17TH CENTURY MATHEMATICS
 |
Logarithms were invented by John Napier, early in the 17th Century |
In the wake of the Renaissance, the 17th Century saw an unprecedented explosion of mathematical and scientific ideas across Europe, a period sometimes called the Age of Reason. Hard on the heels of the “Copernican Revolution” of Nicolaus Copernicus in the 16th Century, scientists like Galileo Galilei, Tycho Brahe and Johannes Kepler were making equally revolutionary discoveries in the exploration of the Solar system, leading to Kepler’s formulation of mathematical laws of planetary motion.
The invention of the logarithm in the early 17th Century by John Napier (and later improved by Napier and Henry Briggs) contributed to the advance of science, astronomy and mathematics by making some difficult calculations relatively easy. It was one of the most significant mathematical developments of the age, and 17th Century physicists like Kepler and Newton could never have performed the complex calculatons needed for their innovations without it. The French astronomer and mathematician Pierre Simon Laplace remarked, almost two centuries later, that Napier, by halving the labours of astronomers, had doubled their lifetimes.
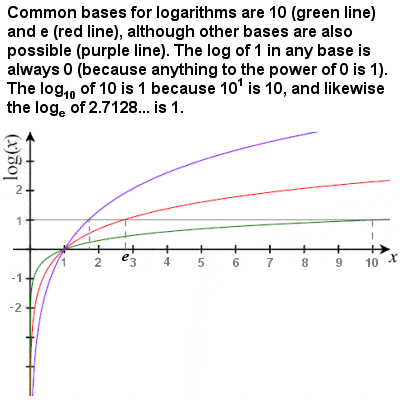
The logarithm of a number is the exponent when that number is expressed as a power of 10 (or any other base). It is effectively the inverse of exponentiation. For example, the base 10 logarithm of 100 (usually written log10 100 or lg 100 or just log 100) is 2, because 102 = 100. The value of logarithms arises from the fact that multiplication of two or more numbers is equivalent to adding their logarithms, a much simpler operation. In the same way, division involves the subtraction of logarithms, squaring is as simple as multiplying the logarithm by two (or by three for cubing, etc), square roots requires dividing the logarithm by 2 (or by 3 for cube roots, etc).
Although base 10 is the most popular base, another common base for logarithms is the number e which has a value of 2.7182818… and which has special properties which make it very useful for logarithmic calculations. These are known as natural logarithms, and are written loge or ln. Briggs produced extensive lookup tables of common (base 10) logarithms, and by 1622 William Oughted had produced a logarithmic slide rule, an instrument which became indispensible in technological innovation for the next 300 years.
Napier also improved Simon Stevin’s decimal notation and popularized the use of the decimal point, and made lattice multiplication (originally developed by the Persian mathematician Al-Khwarizmi and introduced into Europe by Fibonacci) more convenient with the introduction of “Napier’s Bones”, a multiplication tool using a set of numbered rods.
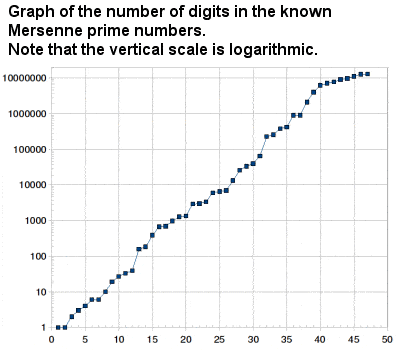 |
Graph of the number of digits in the known Mersenne primes |
Although not principally a mathematician, the role of the Frenchman Marin Mersenne as a sort of clearing house and go-between for mathematical thought in France during this period was crucial. Mersenne is largely remembered in mathematics today in the term Mersenne primes – prime numbers that are one less than a power of 2, e.g. 3 (22-1), 7 (23-1), 31 (25-1), 127 (27-1), 8191 (213-1), etc. In modern times, the largest known prime number has almost always been a Mersenne prime, but in actual fact, Mersenne’s real connection with the numbers was only to compile a none-too-accurate list of the smaller ones (when Edouard Lucas devised a method of checking them in the 19th Century, he pointed out that Mersenne had incorrectly included 267-1 and left out 261-1, 289-1 and 2107-1 from his list).
The Frenchman René Descartes is sometimes considered the first of the modern school of mathematics. His development of analytic geometry and Cartesian coordinates in the mid-17th Century soon allowed the orbits of the planets to be plotted on a graph, as well as laying the foundations for the later development of calculus (and much later multi-dimensional geometry). Descartes is also credited with the first use of superscripts for powers or exponents.
Two other great French mathematicians were close contemporaries of Descartes: Pierre de Fermat and Blaise Pascal. Fermat formulated several theorems which greatly extended our knowlege of number theory, as well as contributing some early work on infinitesimal calculus. Pascal is most famous for Pascal’s Triangle of binomial coefficients, although similar figures had actually been produced by Chinese and Persian mathematicians long before him.
It was an ongoing exchange of letters between Fermat and Pascal that led to the development of the concept of expected values and the field of probability theory. The first published work on probability theory, however, and the first to outline the concept of mathematical expectation, was by the Dutchman Christiaan Huygens in 1657, although it was largely based on the ideas in the letters of the two Frenchmen.
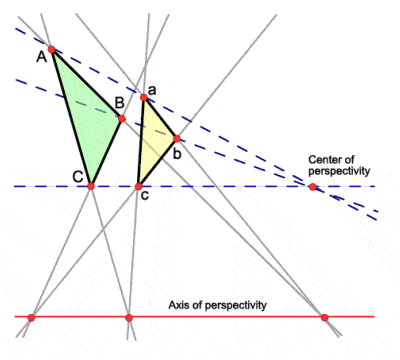 |
Desargues’ perspective theorem |
The French mathematician and engineer Girard Desargues is considered one of the founders of the field of projective geometry, later developed further by Jean Victor Poncelet and Gaspard Monge. Projective geometry considers what happens to shapes when they are projected on to a non-parallel plane. For example, a circle may be projected into an ellipse or a hyperbola, and so these curves may all be regarded as equivalent in projective geometry. In particular, Desargues developed the pivotal concept of the “point at infinity” where parallels actually meet. His perspective theorem states that, when two triangles are in perspective, their corresponding sides meet at points on the same collinear line.
By “standing on the shoulders of giants”, the Englishman Sir Isaac Newton was able to pin down the laws of physics in an unprecedented way, and he effectively laid the groundwork for all of classical mechanics, almost single-handedly. But his contribution to mathematics should never be underestimated, and nowadays he is often considered, along with Archimedes and Gauss, as one of the greatest mathematicians of all time.
Newton and, independently, the German philosopher and mathematician Gottfried Leibniz, completely revolutionized mathematics (not to mention physics, engineering, economics and science in general) by the development of infinitesimal calculus, with its two main operations, differentiation and integration. Newton probably developed his work before Leibniz, but Leibniz published his first, leading to an extended and rancorous dispute. Whatever the truth behind the various claims, though, it is Leibniz’s calculus notation that is the one still in use today, and calculus of some sort is used extensively in everything from engineering to economics to medicine to astronomy.
Both Newton and Leibniz also contributed greatly in other areas of mathematics, including Newton’s contributions to a generalized binomial theorem, the theory of finite differences and the use of infinite power series, and Leibniz’s development of a mechanical forerunner to the computer and the use of matrices to solve linear equations.
However, credit should also be given to some earlier 17th Century mathematicians whose work partially anticipated, and to some extent paved the way for, the development of infinitesimal calculus. As early as the 1630s, the Italian mathematician Bonaventura Cavalieri developed a geometrical approach to calculus known as Cavalieri’s principle, or the “method of indivisibles”. The Englishman John Wallis, who systematized and extended the methods of analysis of Descartes and Cavalieri, also made significant contributions towards the development of calculus, as well as originating the idea of the number line, introducing the symbol ∞ for infinity and the term “continued fraction”, and extending the standard notation for powers to include negative integers and rational numbers. Newton‘s teacher Isaac Barrow is usually credited with the discovery (or at least the first rigorous statrement of) the fundamental theorem of calculus, which essentially showed that integration and differentiation are inverse operations, and he also made complete translations of Euclid into Latin and English.
<< Back to Tartaglia, Cardano & Ferrari | Forward to Descartes >> |
