ISAAC NEWTON: Math & Calculus
 |
Sir Isaac Newton (1643-1727) |
In the heady atmosphere of 17th Century England, with the expansion of the British empire in full swing, grand old universities like Oxford and Cambridge were producing many great scientists and mathematicians. But the greatest of them all was undoubtedly Sir Isaac Newton.
Physicist, mathematician, astronomer, natural philosopher, alchemist and theologian, Newton is considered by many to be one of the most influential men in human history. His 1687 publication, the “Philosophiae Naturalis Principia Mathematica” (usually called simply the “Principia”), is considered to be among the most influential books in the history of science, and it dominated the scientific view of the physical universe for the next three centuries.
Although largely synonymous in the minds of the general public today with gravity and the story of the apple tree, Newton remains a giant in the minds of mathematicians everywhere (on a par with the all-time greats like Archimedes and Gauss), and he greatly influenced the subsequent path of mathematical development.
Over two miraculous years, during the time of the Great Plague of 1665-6, the young Newton developed a new theory of light, discovered and quantified gravitation, and pioneered a revolutionary new approach to mathematics: infinitesimal calculus. His theory of calculus built on earlier work by his fellow Englishmen John Wallis and Isaac Barrow, as well as on work of such Continental mathematicians as René Descartes, Pierre de Fermat, Bonaventura Cavalieri, Johann van Waveren Hudde and Gilles Personne de Roberval. Unlike the static geometry of the Greeks, calculus allowed mathematicians and engineers to make sense of the motion and dynamic change in the changing world around us, such as the orbits of planets, the motion of fluids, etc.
The Average Slope of a Curve
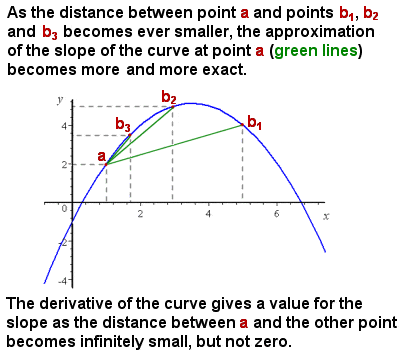 |
Differentiation (derivative) approximates the slope of a curve as the interval approaches zero |
The initial problem Newton was confronting was that, although it was easy enough to represent and calculate the average slope of a curve (for example, the increasing speed of an object on a time-distance graph), the slope of a curve was constantly varying, and there was no method to give the exact slope at any one individual point on the curve i.e. effectively the slope of a tangent line to the curve at that point.
Intuitively, the slope at a particular point can be approximated by taking the average slope (“rise over run”) of ever smaller segments of the curve. As the segment of the curve being considered approaches zero in size (i.e. an infinitesimal change in x), then the calculation of the slope approaches closer and closer to the exact slope at a point (see image at right).
Without going into too much complicated detail, Newton (and his contemporary Gottfried Leibniz independently) calculated a derivative function f ‘(x) which gives the slope at any point of a function f(x). This process of calculating the slope or derivative of a curve or function is called differential calculus or differentiation (or, in Newton’s terminology, the “method of fluxions” – he called the instantaneous rate of change at a particular point on a curve the “fluxion”, and the changing values of x and y the “fluents”). For instance, the derivative of a straight line of the type f(x) = 4x is just 4; the derivative of a squared function f(x) = x2 is 2x; the derivative of cubic function f(x) = x3 is 3x2, etc. Generalizing, the derivative of any power function f(x) = xr is rxr-1. Other derivative functions can be stated, according to certain rules, for exponential and logarithmic functions, trigonometric functions such as sin(x), cos(x), etc, so that a derivative function can be stated for any curve without discontinuities. For example, the derivative of the curve f(x) = x4 – 5x3 + sin(x2) would be f ’(x) = 4x3 – 15x2 + 2xcos(x2).
Having established the derivative function for a particular curve, it is then an easy matter to calcuate the slope at any particular point on that curve, just by inserting a value for x. In the case of a time-distance graph, for example, this slope represents the speed of the object at a particular point.
Method of Fluents
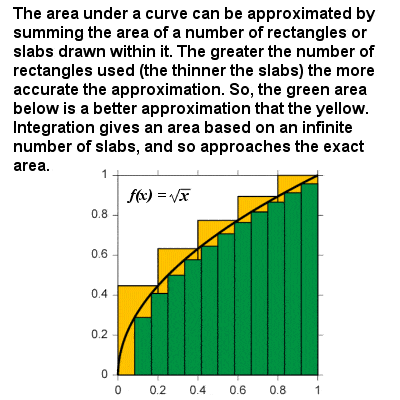 |
Integration approximates the area under a curve as the size of the samples approaches zero |
The “opposite” of differentiation is integration or integral calculus (or, in Newton’s terminology, the “method of fluents”), and together differentiation and integration are the two main operations of calculus. Newton’s Fundamental Theorem of Calculus states that differentiation and integration are inverse operations, so that, if a function is first integrated and then differentiated (or vice versa), the original function is retrieved.
The integral of a curve can be thought of as the formula for calculating the area bounded by the curve and the x axis between two defined boundaries. For example, on a graph of velocity against time, the area “under the curve” would represent the distance travelled. Essentially, integration is based on a limiting procedure which approximates the area of a curvilinear region by breaking it into infinitesimally thin vertical slabs or columns. In the same way as for differentiation, an integral function can be stated in general terms: the integral of any power f(x) = xr is xr+1⁄r+1, and there are other integral functions for exponential and logarithmic functions, trigonometric functions, etc, so that the area under any continuous curve can be obtained between any two limits.
Newton chose not to publish his revolutionary mathematics straight away, worried about being ridiculed for his unconventional ideas, and contented himself with circulating his thoughts among friends. After all, he had many other interests such as philosophy, alchemy and his work at the Royal Mint. However, in 1684, the German Leibniz published his own independent version of the theory, whereas Newton published nothing on the subject until 1693. Although the Royal Society, after due deliberation, gave credit for the first discovery to Newton (and credit for the first publication to Leibniz), something of a scandal arose when it was made public that the Royal Society’s subsequent accusation of plagiarism against Leibniz was actually authored by none other Newton himself, causing an ongoing controversy which marred the careers of both men.
Generalized Binomial Theorem
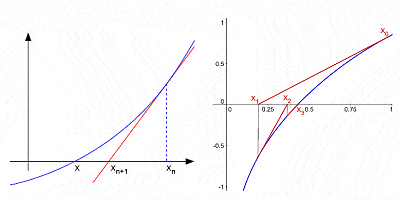 |
Newton’s Method for approximating the roots of a curve by successive interations after an initial guess |
Despite being by far his best known contribution to mathematics, calculus was by no means Newton’s only contribution. He is credited with the generalized binomial theorem, which describes the algebraic expansion of powers of a binomial (an algebraic expression with two terms, such as a2 – b2); he made substantial contributions to the theory of finite differences (mathematical expressions of the form f(x + b) – f(x + a)); he was one of the first to use fractional exponents and coordinate geometry to derive solutions to Diophantine equations (algebraic equations with integer-only variables); he developed the so-called “Newton’s method” for finding successively better approximations to the zeroes or roots of a function; he was the first to use infinite power series with any confidence; etc.
In 1687, Newton published his “Principia” or “The Mathematical Principles of Natural Philosophy”, generally recognized as the greatest scientific book ever written. In it, he presented his theories of motion, gravity and mechanics, explained the eccentric orbits of comets, the tides and their variations, the precession of the Earth’s axis and the motion of the Moon.
Later in life, he wrote a number of religious tracts dealing with the literal interpretation of the Bible, devoted a great deal of time to alchemy, acted as Member of Parliament for some years, and became perhaps the best-known Master of the Royal Mint in 1699, a position he held until his death in 1727. In 1703, he was made President of the Royal Society and, in 1705, became the first scientist ever to be knighted. Mercury poisoning from his alchemical pursuits perhaps explained Newton’s eccentricity in later life, and possibly also his eventual death.
<< Back to Pascal | Forward to Leibniz >> |
