BLAISE PASCAL – Math.
Biography – Who was Pascal
 |
Blaise Pascal (1623-1662) |
The Frenchman Blaise Pascal was a prominent 17th Century scientist, philosopher and mathematician. Like so many great mathematicians, he was a child prodigy and pursued many different avenues of intellectual endeavour throughout his life. Much of his early work was in the area of natural and applied sciences, and he has a physical law named after him (that “pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid”), as well as the international unit for the meaurement of pressure. In philosophy, Pascals’ Wager is his pragmatic approach to believing in God on the grounds that is it is a better “bet” than not to.
But Pascal was also a mathematician of the first order. At the age of sixteen, he wrote a significant treatise on the subject of projective geometry, known as Pascal’s Theorem, which states that, if a hexagon is inscribed in a circle, then the three intersection points of opposite sides lie on a single line, called the Pascal line. As a young man, he built a functional calculating machine, able to perform additions and subtractions, to help his father with his tax calculations.
Pascal’s Triangle
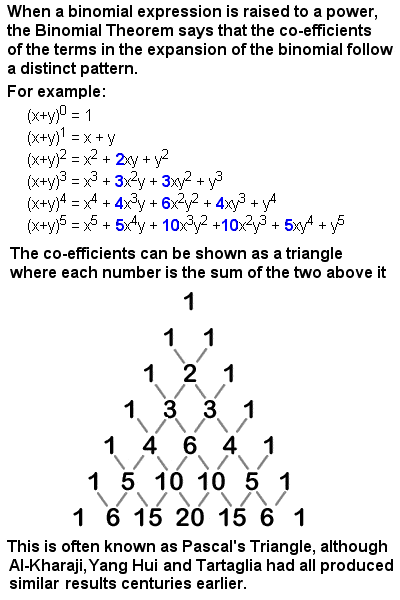 |
The table of binomial coefficients known as Pascal’s Triangle |
He is best known, however, for Pascal’s Triangle, a convenient tabular presentation of binomial co-efficients, where each number is the sum of the two numbers directly above it. A binomial is a simple type of algebraic expression which has just two terms operated on only by addition, subtraction, multiplication and positive whole-number exponents, such as (x + y)2. The co-efficients produced when a binomial is expanded form a symmetrical triangle (see image at right).
Pascal was far from the first to study this triangle. The Persian mathematician Al-Karaji had produced something very similar as early as the 10th Century, and the Triangle is called Yang Hui’s Triangle in China after the 13th Century Chinese mathematician, and Tartaglia’s Triangle in Italy after the eponymous 16th Century Italian. But Pascal did contribute an elegant proof by defining the numbers by recursion, and he also discovered many useful and interesting patterns among the rows, columns and diagonals of the array of numbers. For instance, looking at the diagonals alone, after the outside “skin” of 1’s, the next diagonal (1, 2, 3, 4, 5,…) is the natural numbers in order. The next diagonal within that (1, 3, 6, 10, 15,…) is the triangular numbers in order. The next (1, 4, 10, 20, 35,…) is the pyramidal triangular numbers, etc, etc. It is also possible to find prime numbers, Fibonacci numbers, Catalan numbers, and many other series, and even to find fractal patterns within it.
Pascal also made the conceptual leap to use the Triangle to help solve problems in probability theory. In fact, it was through his collaboration and correspondence with his French contemporary Pierre de Fermat and the Dutchman Christiaan Huygens on the subject that the mathematical theory of probability was born. Before Pascal, there was no actual theory of probability – notwithstanding Gerolamo Cardano’s early exposition in the 16th Century – merely an understanding (of sorts) of how to compute “chances” in dice and card games by counting equally probable outcomes. Some apparently quite elementary problems in probability had eluded some of the best mathematicians, or given rise to incorrect solutions.
It fell to Pascal (with Fermat‘s help) to bring together the separate threads of prior knowledge (including Cardano‘s early work) and to introduce entirely new mathematical techniques for the solution of problems that had hitherto resisted solution. Two such intransigent problems which Pascal and Fermat applied themselves to were the Gambler’s Ruin (determining the chances of winning for each of two men playing a particular dice game with very specific rules) and the Problem of Points (determining how a game’s winnings should be divided between two equally skilled players if the game was ended prematurely). His work on the Problem of Points in particular, although unpublished at the time, was highly influential in the unfolding new field.
The Problem of Points
 |
Fermat and Pascal’s solution to the Problem of Points |
The Problem of Points at its simplest can be illustrated by a simple game of “winner take all” involving the tossing of a coin. The first of the two players (say, Fermat and Pascal) to achieve ten points or wins is to receive a pot of 100 francs. But, if the game is interrupted at the point where Fermat, say, is winning 8 points to 7, how is the 100 franc pot to divided? Fermat claimed that, as he needed only two more points to win the game, and Pascal needed three, the game would have been over after four more tosses of the coin (because, if Pascal did not get the necessary 3 points for your victory over the four tosses, then Fermat must have gained the necessary 2 points for his victory, and vice versa. Fermat then exhaustively listed the possible outcomes of the four tosses, and concluded that he would win in 11 out of the 16 possible outcomes, so he suggested that the 100 francs be split 11⁄16 (0.6875) to him and 5⁄16 (0.3125) to Pascal.
Pascal then looked for a way of generalizing the problem that would avoid the tedious listing of possibilities, and realized that he could use rows from his triangle of coefficients to generate the numbers, no matter how many tosses of the coin remained. As Fermat needed 2 more points to win the game and Pascal needed 3, he went to the fifth (2 + 3) row of the triangle, i.e. 1, 4, 6, 4, 1. The first 3 terms added together (1 + 4 + 6 = 11) represented the outcomes where Fermat would win, and the last two terms (4 + 1 = 5) the outcomes where Pascal would win, out of the total number of outcomes represented by the sum of the whole row (1 + 4 + 6 +4 +1 = 16).
Pascal and Fermat had grasped through their correspondence a very important concept that, though perhaps intuitive to us today, was all but revolutionary in 1654. This was the idea of equally probable outcomes, that the probability of something occurring could be computed by enumerating the number of equally likely ways it could occur, and dividing this by the total number of possible outcomes of the given situation. This allowed the use of fractions and ratios in the calculation of the likelhood of events, and the operation of multiplication and addition on these fractional probabilities. For example, the probability of throwing a 6 on a die twice is 1⁄6 x 1⁄6 = 1⁄36 (“and” works like multiplication); the probability of throwing either a 3 or a 6 is 1⁄6 + 1⁄6 = 1⁄3 (“or” works like addition).
Later in life, Pascal and his sister Jacqueline strongly identified with the extreme Catholic religious movement of Jansenism. Following the death of his father and a “mystical experience” in late 1654, he had his “second conversion” and abandoned his scientific work completely, devoting himself to philosophy and theology. His two most famous works, the “Lettres provinciales” and the “Pensées“, date from this period, the latter left incomplete at his death in 1662. They remain Pascal’s best known legacy, and he is usually remembered today as one of the most important authors of the French Classical Period and one of the greatest masters of French prose, much more than for his contributions to mathematics.
<< Back to Fermat | Forward to Newton >> |
