JUMP TO TOPIC
Factors and Multiples – Differences & Examples
By definition, a factor is a number that divides another number without leaving any remainder. In contrast, a multiple is a number that, when divided a certain of times by another number, no remainder is left.
Illustration
Take for instance, multiplication of;
2 x 5 = 10
2 and 5 are considered to be factors of 10, and similarly, 10 is a multiple of 2 and 5.
What is a factor?
As defined above, a factor is a number that divides a certain number to give out a whole number or integer.For example, 2 is a factor of 8 because it divides 8 without leaving any remainder. 1 is the smallest factor of any number. The factors of 8 are therefore 1, 2, 4, and 8 themselves.
When listing factors of a given number, the first step is to identify all numbers that divide this particular number without a remainder. And to do so, 1 is listed as the first minimum factor. For example, the factors of a number are integers which divide that particular number without a remainder. The number 16 has five factors: 1, 2, 4, 8, and 16. If the number 16 is divided by any of the five numbers, then the resultant is a whole number
The factors of a number are the numbers that divide into it exactly.
For example, the number 12 has six factors:
16 / 2 = 16
16 / 2 = 8
16 / 4 = 4
16 / 8 = 2
16 / 16 = 1
Square Numbers
Square numbers are numbers obtained by multiplying a number by itself. All square numbers have an odd number of factors.
For example, 4 has 3 factors, 16 has 5 factors
Prime Numbers
A prime number is only divisible by 1 and itself. Therefore, prime numbers have only two factors. Prime numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29 have only two factors.
What is a Multiple?
A multiple is the product of two integers. 3 x 7 = 21, in this case, is a multiple of 3 and 7. All integers have the number itself and zero as their multiple.
Multiples of a given number are found by multiplying that number by number 1. The resultant answer after the multiplication is, therefore, the multiple of that number.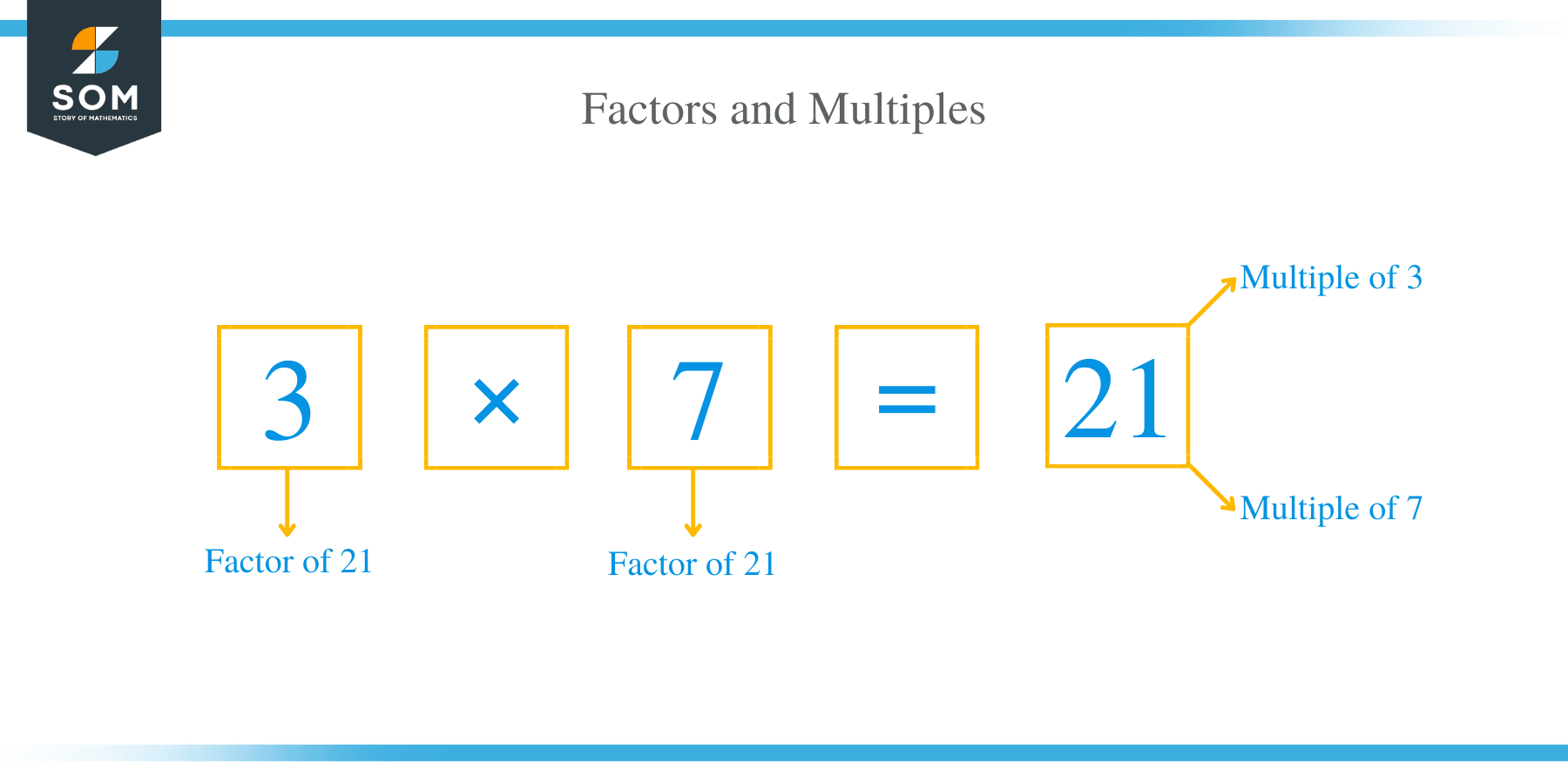
Common Multiples
A common multiple of a number is a multiple of two or more numbers.
To find the common multiples, the following steps are followed.
- List all multiples for each number.
- Proceed with your list until at least two multiples are common to all the lists.
- Select the common multiples.
Multiples of 2 are obtained as:
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
And so forth. Multiples of 2 will be: 0, 2, 4, 6, 8 or 10.
Multiples of 3 are:
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
and so on.
Multiples of 5 include:
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
and so on. You can realize that every multiple of 5 ends with either 5 or 0.
What are the differences between a factor and a multiple?
| Factor | Multiple | |
| 1 | A list of numbers, each of which can divide a certain number without leaving a remainder. | A list of number which is a result of a multiplication of the number |
| 2 | A number that can be multiplied with a particular integer to get another integer | The product is obtained by multiplication of the number by an integer. |
| 3 | Factors are a number are limited | Multiples are endless |
| 4 | Factors are generally less or equal to the number | Multiples are greater or equal to the given number. |
| 5 | Factors are obtained by division | Multiples s are obtained by multiplication |
Example 1
Which of the following statements are true or false?
- 9 is a multiple of 3
- 5 is a factor of 15.
- 7 is a multiple of 21.
- 13 is a factor of 25
Solution
9 is a multiple of 3 is true because 3 x 3 = 9.
5 is a factor of 15 is true because: 5 x 3 = 15.
7 is a multiple of 21 is false because many are always greater than equals that number.
13 is a factor of 25 is false because you can’t multiply a whole number by 13 to get 25.
Example 2
“10 is a factor of 50”? Which of the following phrases are true to this statement.
- 50 is divisible by 10
- 10 is divisible by 50
- 10 is a multiple of 50
- 50 is a multiple of 10
Solution
Factors are numbers you multiply to obtain larger ones, so it true to say 50 is divisible by 10. Multiples are bigger numbers obtained when you multiply two factors, so it possible to say that 50 is a multiple of 10.
Hence, only options a and d are correct.
Example 3
Identify the are true or false statement from the following list.
- 5 is a factor of 105
- 3 is a multiple of 121
- 88 is a multiple of 9
- 11 is a factor of 121
Solution
- True, because 5 × 21 = 105.
- False, because 121 is a multiple of 3, and so, 3 is a factor of 121.
- This statement is not true because 88 is not divisible by 9.
- The statement is true because: 11 x 11 = 121.
Example 4
List down all factors of 1000.
Solution
The factors of 1000 are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 125, 200, 250, 500 and 1000.
Example 5
List down all multiples of 8 upto 1000?
Solution
The multiples of 8 upto 1000 include:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96,104, 112, 120, 128, 136, 144, 152, 160, 168, 176, 184, 192,200, 208, 216, 224, 232, 240, 248, 256, 264, 272, 280, 288, 296,304, 312, 320, 328, 336, 344, 352, 360, 368, 376, 384, 392,400, 408, 416, 424, 432, 440, 448, 456, 464, 472, 480, 488, 496,504, 512, 520, 528, 536, 544, 552, 560, 568, 576, 584, 592,600, 608, 616, 624, 632, 640, 648, 656, 664, 672, 680, 688, 696,704, 712, 720, 728, 736, 744, 752, 760, 768, 776, 784, 792,800, 808, 816, 824, 832, 840, 848, 856, 864, 872, 880, 888, 896,904, 912, 920, 928, 936, 944, 952, 960, 968, 976, 984, 992, 1,000.
Example 6
The number 16 is divisible by 4, so which of these two numbers is a multiple and a factor and why?
Solution
16 is a multiple because it is bigger, whereas 4 is a factor because it is smaller.
