Prime Factorization – Explanation & Examples
Prime factorization is a method of finding all the prime numbers that multiply to form a number. Factors are multiplied to get a number, while prime factors are the numbers that can only be divided by 1 or themselves.
How to find Prime Factorization?
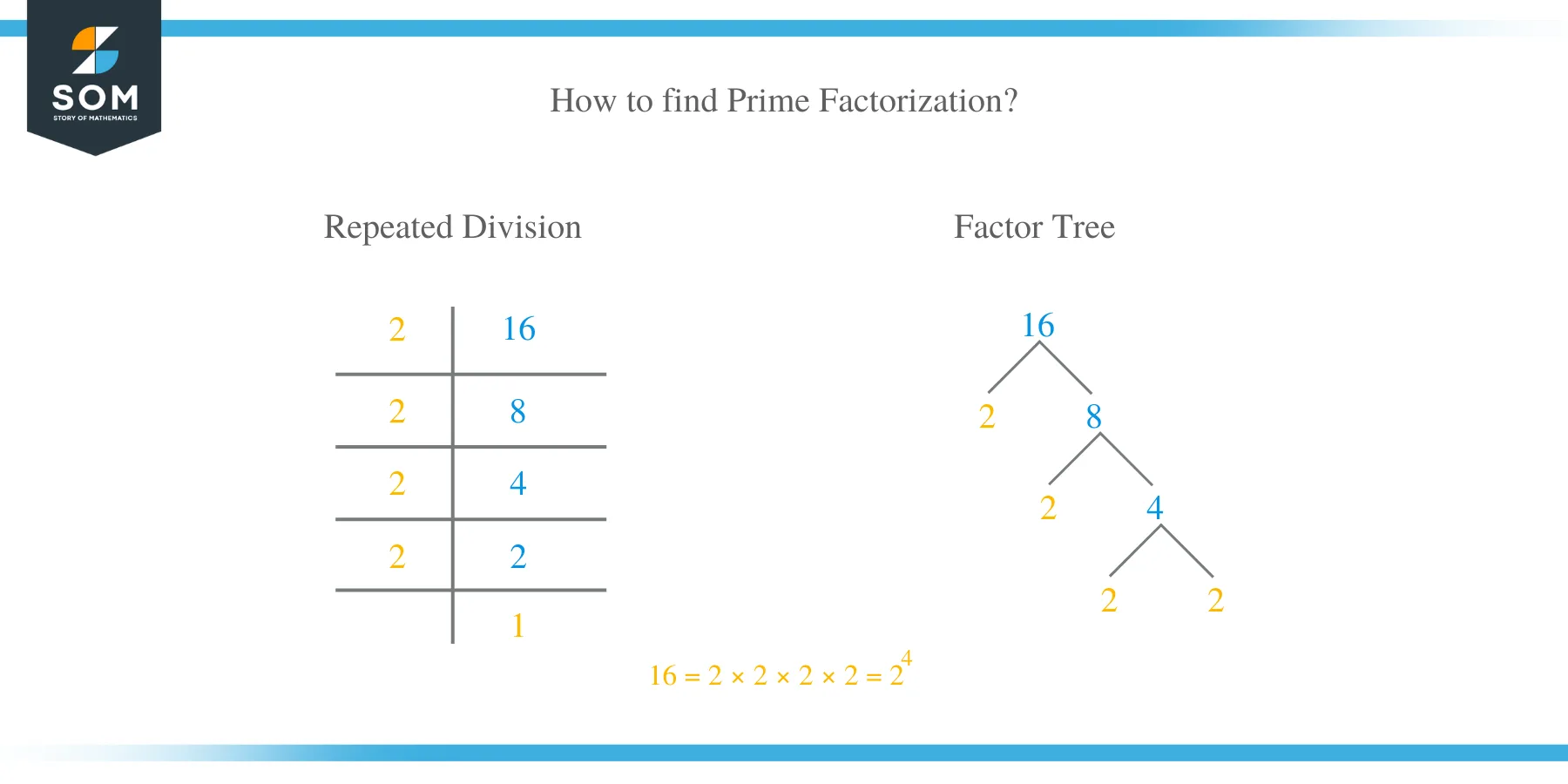
There are two methods of finding prime factors of a number. These are repeated division and factor tree.
Repeated division
A number is reduced by dividing it severally with prime numbers. Prime factors of number 36 are found by repeated division as shown:
The prime factors of number 36 are, therefore, 2 and 3. This can be written as 2 × 2 × 3 × 3. It is advisable to start dividing a number by the smallest prime number and proceed to bigger factors.
Example 1
What are the prime factors of 16?
Solution
The best way to solve this problem is by identifying the smallest prime factor of the number, which is 2.
Divide number by 16;
16 ÷ 2 = 8
Because 8 is not a prime number, proceed by dividing again by the smallest factor;
8 ÷ 2 = 4
4 ÷ 2 = 2
We have the prime factors of 16 highlighted in yellow, and they include: 2 x 2 x 2 x 2.
which can be written as an exponent:
16 = 2 2
Example 2
Find the prime factors of 12.
Solution
Divide 12 by 2;
12 ÷ 2 = 6
6 is not prime, proceed;
6 ÷ 2 = 3.
Therefore, 12 = 2 x 2 x 3
12 = 2 2 × 3
It is noted that, all prime factors of a number are prime.
Example 3
Factorize 147.
Solution
Start by dividing 147 by the smallest prime number.
147 ÷ 2 = 73.5
Our answer isn’t an integer, try the next prime number 3.
147 ÷ 3 = 49
Yes, 3 worked, now proceed to the next prime that can divide 49.
49 ÷ 7 = 7
Therefore, 147 = 3 x 7 x 7,
=3 x 7 2.
Example 4
What is the prime factorization of 19?
19 = 19
Solution
Another method on how to perform factorization is to break a number down into two integers. Now find the prime factors of the integers. This technique is useful when dealing with bigger numbers.
Example 5
Find the prime factors of 210.
Solution
Break down 210 into:
210 = 21 x 10
Now calculate the factors of 21 and 10
21 ÷ 3 = 7
10 ÷ 2 = 5
Combine the factors: 210 = 2 x 3 x 5 x 7
Factor tree
Factor tree involves finding the prime factors of a number by drawing tree- like programs. Factor tree is the best tool of doing prime factorization. The prime factors of 16 are obtained by factor tree as shown below:
