JUMP TO TOPIC
Greatest Common Factor|Definition & Meaning
Definition
The greatest common factor (or GCF) of two numbers is the largest factor shared by both numbers. Dividing the two numbers by the GCF always produces an integer for each one.
Both share a few factors once all the numbers’ components have been identified.
The largest common factor is the one with the largest number among the common factors. HCF (Highest Common Factor) is another name for the GCF.
A factor is a quantity that produces the required quantities when multiplied by several other quantities. Factors are another name for the total that results. The numbers may often be factored into a variety of combinations.
Figure 1 below shows the GCF of 18.
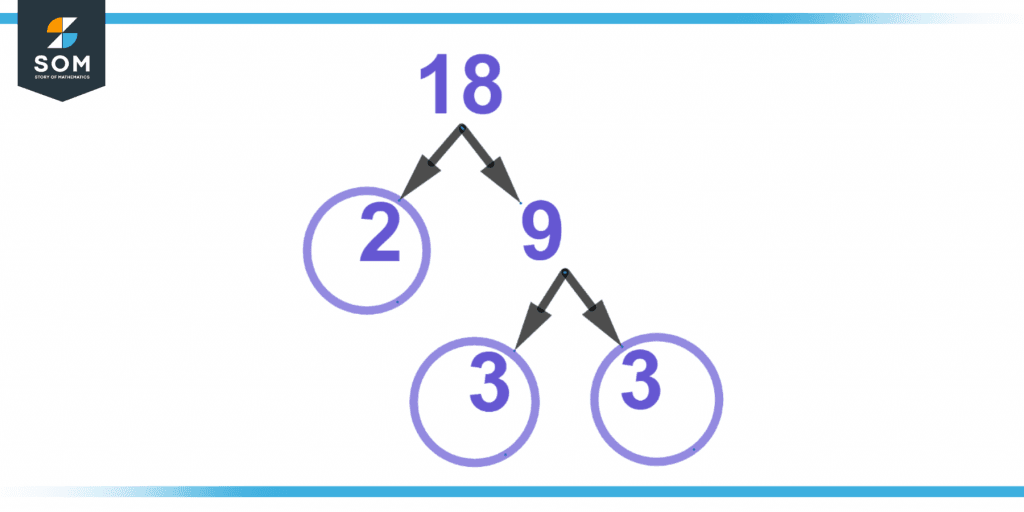
Figure 1 – Representation of the greatest common factor of 18.
How To Find the Greatest Common Factor?
We must first list each pair of digits’ prime factors to obtain the GCF for that pair. Multiplying the common features between the two numbers yields GCF. If there are no additional shared prime factors, the largest common denominator is 1. Numerous techniques may be used to figure out the GCF of two digits.
One of the simplest ways to determine the greatest common factor of two or more numbers is to use the prime factoring method.
The determination of the GCF of the given number set can be straightforward. But a few steps need to be followed to get the proper GCF. Before you can figure out the greatest component that any given number has in common, you must first figure out all of its components.
Figure 2 shows the GCF of 21.

Figure 2 – Representation of GCF of 21.
The GCF of two numbers can be calculated in several ways. By applying the prime factorization method, you can quickly get the GCF of two or more integers.
Finding the provided numbers’ highest common factor can be done through various methods. No of the approach, the GCF of the numbers will always give the same result. The GCF of two numbers can be calculated in one of three ways:
- GCF, through listing factors
- GCF by prime factorization
- GCF division approach
Listing Factors Method for Greatest Common Factor
This approach involves listing each number’s elements and then identifying their shared factors. The most significant common factor among all the factors is then identified.
Prime Factorization With Greatest Common Factor
We employ the below techniques to determine the GCF of integers using the prime factorization method. Let’s use the example below to understand this procedure.
- Step 1 is to identify the numbers that have common prime factors.
- Step 2: To find the GCF of those integers, multiply these frequent prime factors.
Method of Greatest Common Factor by Division
The division technique may be used to get the GCF of two integers. Let’s break this down using the steps below and the example.
- Step 1: In this process, divide the bigger by, the smaller number, then determine the remaining.
- Step 2: Next, we split the remaining amount from the previous step into a new number, now the new dividend. We then divide again using long division.
- Step 3: We perform long division until the remainder equals 0. It should be remembered that the GCF of those two values will serve as the final divisor.
Figure 3 below shows GCF of 162 by division method.
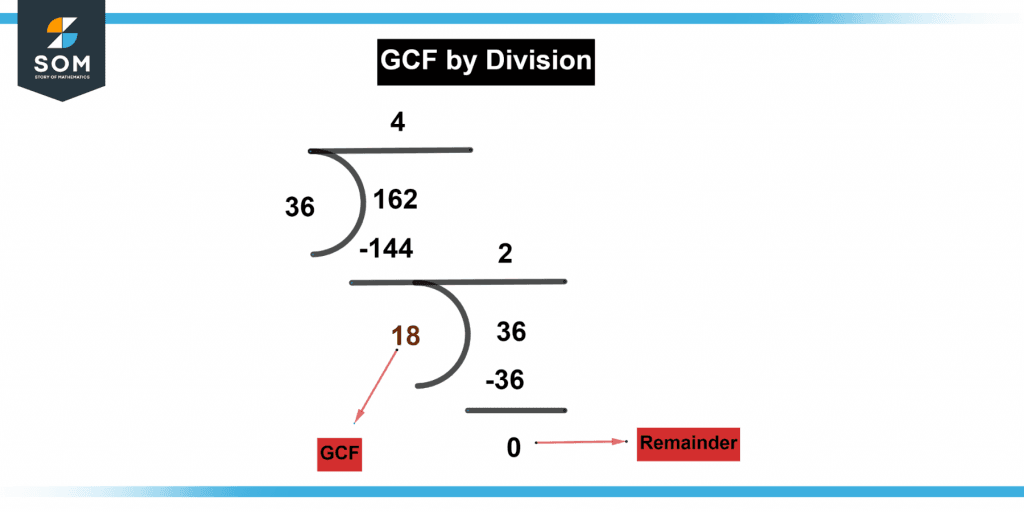
Figure 3 – Representation of GCF by division.
Multiple Numbers of a Greatest Common Factor
We may use either the “listing factors method” or the “prime factorization technique” to determine the GCF of several integers. However, there is little difference when dealing with several integers when utilizing the division approach.
Greatest Common Factor of Three Numbers
We follow the steps below to determine the three-digit GCF. Let’s use the steps and example below to understand this.
- Step 1: Determine the GCFs of the two largest and smallest numbers provided.
- Step 2: After determining the GCF of the first two digits in Step 1, find the GCF of the third number.
- Step 3: This displays the three digits GCF.
Greatest Common Factor of Prime Numbers
As far as we know, a prime quantity only contains two elements: 1 and the absolute amount. Let’s examine the prime elements 11 & 13, whose GCF may be determined by listing their constituent parts.
The components of 11 are 1, 11, & 13, respectively, are 1 and 13. The only thing that 11 & 13 have in common is 1. Consequently, the prime value’s GCF is always 1.
Qualities of Greatest Common Factors
The GCF of x & y is traditionally understood to be the GCF between the digits a and b. Let’s look at some of the essential GCF attributes:
- Each number in a GCF greater than two is divided equally and without surplus.
- The GCF of one or more numbers is the component of each number.
- In most cases, the GCF of two integers or more is less than or equal to every one of the integers.
- The GCF is always 1, even though there are two or more prime factors.
Examples of Greatest Common Factors
Here are a few examples of the greatest common factors that will further help clarify the concept.
Example 1
A college student needs to find the GCF of 6, 72, and 120 using the method of listing the factors.
Solution
The numbers 6, 72, and 120 are given. We will find the parts of each of these integers, and then we will see the GCF.
The number 6 is the only link between the numbers 72 and 120. Thus, the GCF for 6, 72, and 120 is 6.
Example 2
While working on an assignment, a high school must find the GCF of the prime numbers 17 & 19. Using the methods above, find the GCF of the prime numbers.
Solution
First, let’s list the components of 17 = 1, then we can determine the GCF of 17 & 19. Let’s now identify the components that make 19 equal 1. We can observe that between 17 and 19, there is just one component in common. The GCF of 17 & 19 is thus 1.
All Images are made using GeoGebra.
