Fractions – Definition & Types

The word “fraction” is derived from the Latin word fractus, which means the number representing part of the whole or any number of parts. In layman language, a fraction is a number that describes the size of parts of a whole unit. These sizes can be one-half, three-quarters, and a third, etc.

A fraction is normally written in two parts, where the numerator is displayed above a line or before a slash whereas, the denominator is displayed below or before the line.

The terms numerator and denominator are also used in other fractions such as complex, compound, mixed and complex fractions.

What are Fractions?

A fraction can be defined as a number that represents a whole number that has been divided into equal parts.

For example, if you have an orange and cut it into 4 equal slices, 1 of those slices is written: 1/4.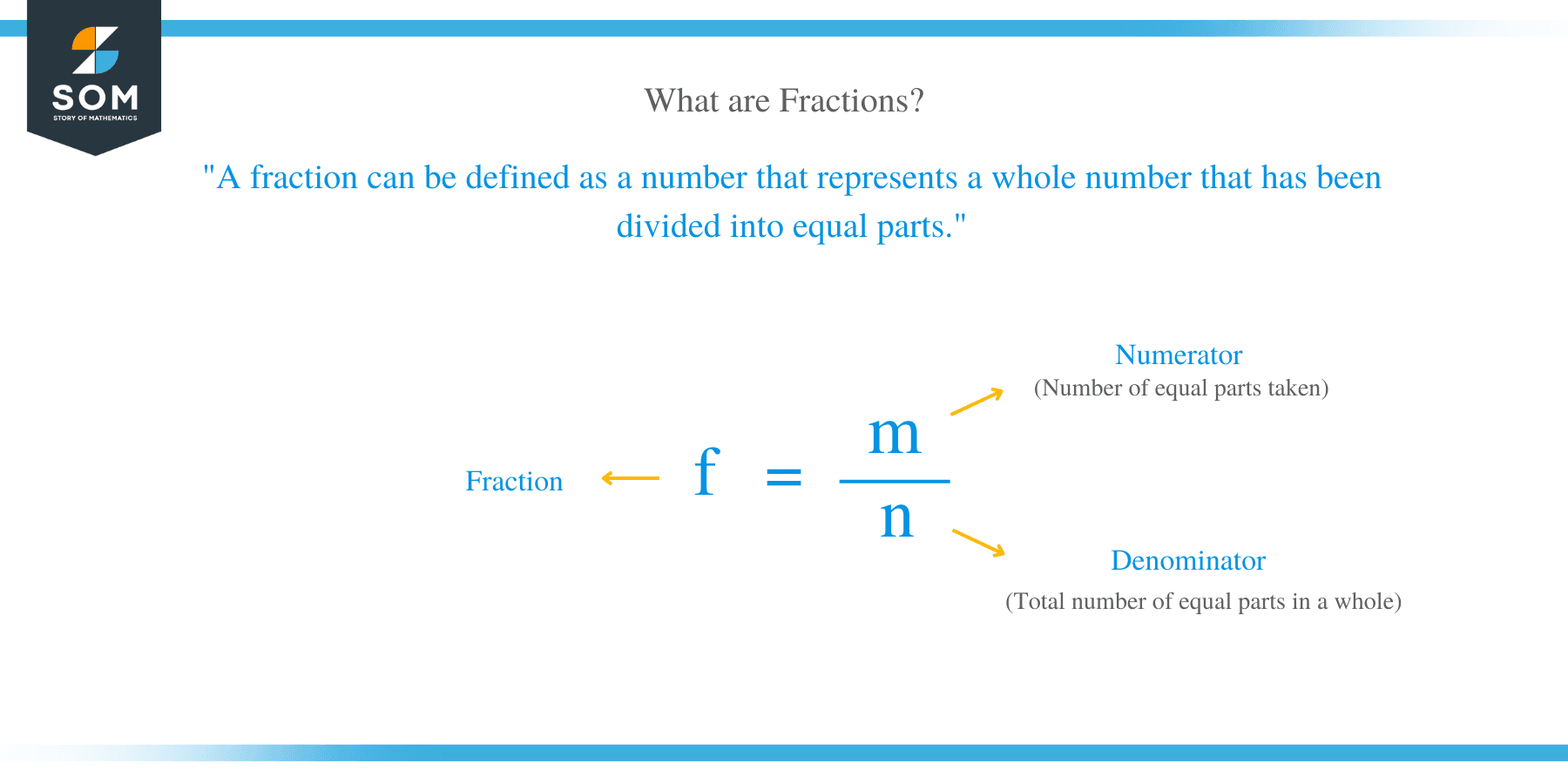

What are Proper Fractions?

A proper fraction is a fraction in which the numerator is less than the denominator. In other words, a proper fraction is less than 1.

Examples of proper fractions are:

1/2, 2/3, 2/7, 4/7, 5/11, 15/26, 50/97, etc.

A fraction is said to be an improper fraction when its denominator is smaller than its numerator.

What are improper fractions?

A fraction is said to be an improper fraction when its denominator is smaller than its numerator. This fraction is generated by the addition of a whole number and one proper fraction. The fractions 11/5, 23/9, 18/5, 3/2, 9/8, etc., are the fractions where the denominators are smaller than the numerators.

For example:

(i) 1 + 4/3 = 3/3 + 4/3 = (3 + 4)/3 = 7/3

(ii) 3 + 5/7 = (3 × 7)/7 + 5/7 = (21 + 5)/7 = 26/7

Similarly, fractions such as:13/5, 27/9, 5/3, 17/2, 9/7 are called improper fractions.

What are Mixed Fractions?

A mixed fraction is a fraction in which a whole number and a proper fraction have been combined. Examples of mixed fractions are 1^1/₃, 5 ^{2 /}_3, 6^1/_2, etc.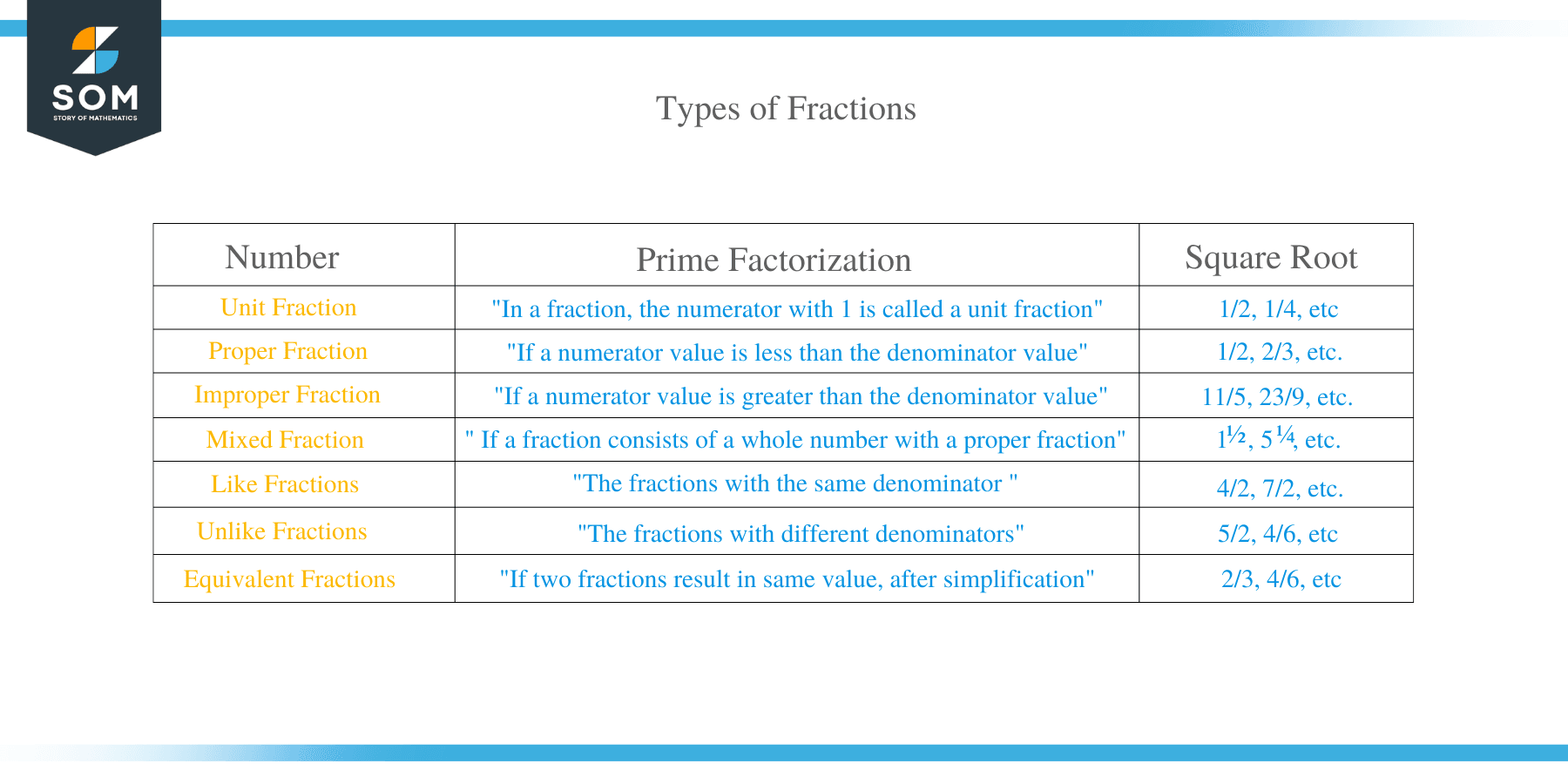

How to convert improper fraction to mixed fraction?

To convert an improper fraction into a mixed fraction, the numerator is divided by the denominator, and the quotient written as a whole number, and the remainder as the numerator.

Example 1

Convert 17/4 as a mixed fraction.

Solution

To solve this problem, these are the steps undertaken

• Divide the numerator by the denominator.
• The quotient is 4, and the remainder is 1.
• Combine the whole number 4 with the fraction 1/4
• 4 ^1/₄ is the mixed fraction.

 

Example 2

Convert 14/9 to a mixed fraction.

Solution

• Begin by dividing the numerator by the denominator
• 14/9 = 1 and 5 as the remainder.
• Take 1 as the whole number and 5 as the numerator,
• Write down the fraction as: 14/9 = 1 ^5/₉

Note: If during division, there is no remainder, then take the quotient as a whole number.

Example 3

Convert the fraction 20/5 to a mixed fraction.

Solution

• Divide the numerator by the denominator.
• 20/5 =4
• The quotient is 4, and there is no remainder. Therefore, take 4 as the answer.
• 20/5 = 4

How to convert mixed fractions as a proper fraction?

A mixed fraction can be expressed as a proper fraction. This I did by multiplying the fraction’s denominator with the whole number, and the product added to the numerator.

For example, to convert a mixed fraction 2 ^1/₃ to an improper fraction, the following steps are followed:

• Multiply the denominator by the whole number.
• For this case, 2 is the whole number and 3 is the denominator,
• 2 x 3 = 6
• Add the product to the numerator
• 6 + 1 =7
• Now the numerator changes to 7 and the denominator remains 3.
• Write the result an improper fraction as 7/3.

Take another example, suppose we want to convert 5^2/₃ to an improper fraction.

These are the steps:

• • First of all, multiply the denominator by the whole number and add this product to the numerator.
  • 3 x 5 = 15
  • Add the numerator to the product
  • 15 + 2 = 17
  • Write fraction by taking 17 as the new numerator while 5 remaining as the denominator.
  • The result is 17/5