Geometric Sequence – Pattern, Formula, and Explanation

Geometric sequences are a series of numbers that share a common ratio. We cab observe these in population growth, interest rates, and even in physics! This is why we understand what geometric sequences are.

Geometric sequences are sequences of numbers where two consecutive terms of the sequence will always share a common ratio.

We’ll learn how to identify geometric sequences in this article. We’ll also learn how to apply the geometric sequence’s formulas for finding the next terms and the sum of the sequence.

We’ll also learn how to identify geometric sequences from word problems and apply what we’ve learned to solve and address these problems. So, let’s begin by understanding the definition and conditions of geometric sequences.

What is a geometric sequence?                

Geometric sequences are sequences where the term of the sequence can be determined by multiplying the previous term with a fixed factor we call the common ratio.

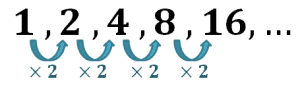
The sequence above shows a geometric sequence where we multiply the previous term by $2$ to find the next term.

That’s why we have the following terms:

\begin{aligned} 1 \times 2 &= 2\\2 \times 2 &= 4\\4 \times 2 &= 8\\8 \times 2 &= 16\\.\\.\\. \end{aligned}

This shows that this sequence has a common ratio of $2$.

Let’s look at another way of understanding geometric sequences and common ratios by the figure shown below.

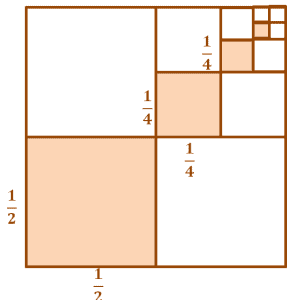
This figure is a visual representation of terms from a geometric sequence with a common ratio of $\dfrac{1}{2}$. We can find the smaller square dimensions by taking half of the length of the previous dimensions.

\begin{aligned} 1 \times \color{green}\dfrac{1}{2} &= \dfrac{1}{2}\\\dfrac{1}{2} \times \color{green}\color{green}\dfrac{1}{2} &= \dfrac{1}{4}\\\dfrac{1}{4} \times \color{green}\color{green}\dfrac{1}{2} &= \dfrac{1}{8}\\.\\.\\. \end{aligned}

This means that when you’re having a memory lapse and need a quick refresher of what a geometric sequence is – it helps to remember how it’s like when we fold papers into a half fold over and over again.

Geometric sequence definition            

Now that we have an idea of what a geometric sequence is, we should define it formally so that we have its general form and we can use it to work on all types of geometric sequences.

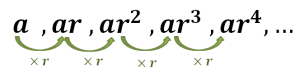
Let’s say the first term of the sequence is $a$ and the sequence has a common ratio of $r$, and the second term can be determined by multiplying $a$ by $r$. This process continues throughout the entire process.

Keep in mind as well that $r$ can either be an integer or a rational factor.

• When $|r| < 1$, the next term becomes smaller (disregarding the sign of the term).
• When $|r| > 1$, the next term becomes bigger (disregarding the sign of the term).

Here are four more examples of geometric sequences. We’ll observe what happens when $a$ is positive and when $r$ is a whole number or a rational one.

These examples can help us better understand how the signs of the first term and the value of the common ratio affect the next terms. From this, we can also see that the terms of a geometric sequence drastically increase or decrease because we’re working with the common ratio’s powers, $r$.

How to solve geometric sequences?                

There are different approaches to finding the unknown elements of a geometric sequence. The most important step is finding the common ratio shared by the sequence since, in most formulas, $r$ is essential.

We’ll slowly dive right into these different formulas and understand when they are most useful in the next sections. Why don’t we begin with learning how we can find $a_n$.

Geometric sequence formula

In this section, we’ll learn how to find the nth term, $a_n$, of a geometric sequence by expressing $a_n$ using the explicit and recursive rules.

Recursive Rule

We can find any term from the sequence using the recursive rule. For this, we’ll need the term before $a_n$ and the common ratio to find the value of $a_n$.

\begin{aligned}a_n = a_{n – 1} \cdot r\end{aligned}

This makes sense since we need to multiply the previous term, $a_{n-1}$, by the common ratio, $r$, to find the value of the next term, $a_n$.

We can also use this rule to find an expression for $r$ in terms of $a_{n – 1}$ and $a_n$.

\begin{aligned}r = \dfrac{a_n}{a_{n – 1}}\end{aligned}

However, this form has its limitations, especially when we want to find, let’s say, the $40$th term of a sequence. This is also why we need to learn about the explicit rule.

Explicit Rule

Let’s begin by observing the general expressions for the terms of a geometric sequence.

\begin{aligned} a_1 &= a\\a_2 &= a \cdot r\\a_3 &= ar \cdot r\\&= ar^2\\a_4&= ar^2 \cdot r\\&= ar^3\\.\\.\\.\end{aligned}

Notice anything? To find the nth term, we multiply the first term by the ratio raised to the $(n – 1)$th term.

This means that if we continue the equations show above and include $a_n$, we have the explicit rule shown below.

$\begin{aligned}a_n = a_1 r^{n -1}\end{aligned}

This rule is more flexible than the recursive rule, and it would be important for us to remember this rule.

How to find the sum of the geometric sequence?

We’ve just learned how to find the nth term of the geometric sequence, so it’s time for us to learn how to find the sum of a geometric series.

Remember the difference between the arithmetic series and arithmetic sequence? The same reasoning applies concerning the difference between the geometric series and sequence.

Given the general form of a geometric sequence, $\{a_1, a_2, a_3, …, a_n\}$, the general form of a geometric series is simply $ a_1 + a_2 + a_3 + … + a_n$.

To find this series’s sum, we need the first term and the series’s common ratio.

\begin{aligned}S_n = \dfrac{a_1(1 – r^n)}{1 – r}\end{aligned}

We can also find the sum of an infinite geometric series, $a_1 + a_2 + a_3 + …$, using the first term and the common ratio.

\begin{aligned}S_{\infty} = \dfrac{a_1}{1 – r}\end{aligned}

 We can only use this if we want to find the sum of an infinite geometric series with a common ratio between $-1$ and $1$.

Now that we’ve learned everything we need to know about geometric sequences and series, why don’t we apply this in the problems below?

Example 1

Calculate the common ratios of the following geometric sequence and find the next two terms of the sequence.

a. $2, 6, 18, …$
b. $-1, -4, -16, …$
c. $\dfrac{1}{3}, -\dfrac{1}{9}, \dfrac{1}{27},…$

Solution

Let’s observe the common ratios for each sequence by dividing the next term by the previous term. Once we have this ratio, we can find the next two terms by multiplying the last term with this ratio.

Beginning with $2, 6, 18, …$, we have:

\begin{aligned} r &= \dfrac{6}{2}\\&= 3\\r&= \dfrac{18}{6}\\&= 3\end{aligned}

This means that the common ratio of this geometric sequence is $3$. To find the next two terms, we simply multiply $18$ by $3$ and do the same for the next term.

\begin{aligned}18 \times 3 &=\boldsymbol{54 }\\ 54\times 3 &= \boldsymbol{162}\end{aligned}

Now, let’s work on the second geometric sequence, $-1, -4, -16, …$.

\begin{aligned} r &= \dfrac{-4}{-1}\\&= 4\\r&= \dfrac{-16}{-4}\\&= 4\end{aligned}

This shows that this geometric sequence will have a common ratio of $4$. We can use this to find the next two terms as shown below.

\begin{aligned}-16\times 4 &=\boldsymbol{-64 }\\ -64\times 4 &= \boldsymbol{-256}\end{aligned}

Let’s move on to the last geometric sequence, $\dfrac{1}{3}, -\dfrac{1}{9}, \dfrac{1}{27},…$.

\begin{aligned} r &= \dfrac{-\dfrac{1}{9}}{\dfrac{1}{3}}\\&= -\dfrac{1}{3}\\r &= \dfrac{\dfrac{1}{27}}{-\dfrac{1}{9}}\\&= -\dfrac{1}{3}\end{aligned}

Hence, the third geometric sequence has a common ratio of $-\dfrac{1}{3}$, so we can use this to find the next two terms.

\begin{aligned}\dfrac{1}{27} \times -\dfrac{1}{3} &=\boldsymbol{-\dfrac{1}{81} }\\ -\dfrac{1}{81} \times -\dfrac{1}{3} &=\boldsymbol{\dfrac{1}{243} }\end{aligned}

Example 2

What is the tenth term of the sequence $\dfrac{1}{4}, \dfrac{1}{2}, 1, 2, …$?

Solution

Our approach in our previous example might be tedious if we want to find the tenth term of the sequence that we have now, so instead, let’s use the explicit rule to the 10^th term.

Recall that $a_n = a_1 r^{n-1}$, where for our problem, $a_1 = \dfrac{1}{4}$ and $n = 10$.

We still need to find the value of the common ratio, $r$, by inspecting the terms and dividing the next term by the previous one, as shown below.

\begin{aligned} r &= \dfrac{\dfrac{1}{2}}{\dfrac{1}{4}}\\&= 2\\r &= \dfrac{1}{\dfrac{1}{2}}\\&= 2\end{aligned}

Now that we have $r = 2$, we can now use the explicit rule to find the tenth term’s value.

\begin{aligned}a_{10} &= \dfrac{1}{4} \cdot 2^{10 – 1}\\&= \dfrac{1}{4} \cdot 2^{9}\end{aligned}

You can continue by expanding $2^9 = 512$, but it’ll be easier if we express $4$ as $2^2$. This way, we can use the exponent property, $\dfrac{b^n}{b^m} = b^{n – m}$ to simplify the expression.

\begin{aligned}a_{10} &= \dfrac{1}{2^2} \cdot 2^{9}\\&= \dfrac{2^9}{2^2}\\&= 2^7\\&= 128\end{aligned}

Hence, the tenth term of the sequence, $\dfrac{1}{4}, \dfrac{1}{2}, 1, 2, …$, is equal to $128$.

Example 3

Find the second and third terms of a geometric sequence if its first and the fourth terms are $-5$ and $-135$?

Solution

We’re only given the first and the fourth terms of the sequence – $a_1$ and $a_4$. We need to find $a_2$ and $a_3$.

Why don’t we use the explicit rule, $a_n = a_1 r^{n – 1}$, to express $a_4$ in terms of $a_1$. We can then solve for $r$ by simplifying the resulting equation.

\begin{aligned}a_4 &= a_1 r^{4 – 1}\\a_4 &= a_1 r^3\\-135&= -5r^3\\r^3 &= \dfrac{-135}{-5}\\r^3&= 27\\ r&=3\end{aligned}

Now that we have the common ratio, we can now find the second and third terms by multiplying $-5$ by $3$ and do the same for the third term.

\begin{aligned}a_2 &= a_1 \cdot 3\\&= -5(3)\\&=-15\\a_3 &= a_2 \cdot 3\\&= -15(3)\\&=-45\end{aligned}

This means that the second and third terms are $-15$ and $-45$, respectively.

Example 4

Find the sum of the following infinite and finite geometric series.

a. $64 + 16 + 4 + 1 + …$
b. $-12 + -6 + -3 + -\dfrac{3}{2} + …$
c. $2 + 4 + 8 + 16 + … + 1024$
d. $\dfrac{1}{27} + \dfrac{1}{9} + \dfrac{1}{3} + 1 + … + 81$

Solution

The first two series are infinite geometric series, so we’ll only need the first and common ratios for each series. Recall that the formula for the sum of infinite series is $S_{\infty} = \dfrac{a_1}{1 – r}$, where $-1 < r < 1$.

Let’s work on the first series, we have $64 + 16 + 4 + 1 + …$. Divide the next term by the previous one to find the common ratio, $r$.

\begin{aligned}r &= \dfrac{16}{64}\\&= \dfrac{1}{4}\\r &= \dfrac{4}{16}\\&= \dfrac{1}{4}  \end{aligned}

Since $r = \dfrac{1}{4}$ and is within the allowed range; we can apply the formula for the sum of infinite series.

\begin{aligned}S_{\infty} &= \dfrac{a_1}{1 – r}\\&= \dfrac{64}{1 – \dfrac{1}{4}}\\&= \dfrac{64}{\dfrac{3}{4}}\\&= 64 \cdot \dfrac{4}{3}\\&= \dfrac{256}{3}\end{aligned}

We can apply a similar process for the second infinite series, so let’s go ahead and observe its common ratio.

\begin{aligned}r &= \dfrac{-6}{-12}\\&= \dfrac{1}{2}\\r &= \dfrac{-3}{-6}\\&= \dfrac{1}{2}  \end{aligned}

The common ratio, $r = \dfrac{1}{2}$, is also within the allowed range for $r$, so we can use the same formula to find the sum of $-12 + -6 + -3 + -\dfrac{3}{2} + …$.

\begin{aligned}S_{\infty} &= \dfrac{a_1}{1 – r}\\&= \dfrac{-12}{1 – \dfrac{1}{2}}\\&= \dfrac{-12}{\dfrac{1}{2}}\\&= -12 \cdot \dfrac{2}{1}\\&= -24\end{aligned}

The third series is a finite geometric series. We know this because the series has an end and meaning, has a value for $a_n$ and $n$. For this kind of series, we’ll use the formula $S_n =\dfrac{a_1(1 – r^n)}{1- r}$.

Using the explicit rule for the nth term, $a_n$, we’ll be able to confirm the number of terms present in $2 + 4 + 8 + 16 + … + 1024$.

First, let’s determine the common ratio shared by the series.

\begin{aligned}r &= \dfrac{4}{2}\\&= 2\\r &= \dfrac{8}{4}\\&= 2\end{aligned}

We have $r=2$, $a_1 = 2$, and $a_n = 1024$, so let’s substitute these values and find the value of $n$ using $a_n = a_1 \cdot r^{n – 1}$.

\begin{aligned}a_n &= a_1 \cdot r^{n – 1}\\1024 &= 2(2)^{n-1}\end{aligned}

We can express $1024$ as a power of $2$ so that we can equate the exponents and solve for $n$.

\begin{aligned}2^{10} &= 2(2)^{n-1}\\2^{10} &= 2^{1 + n – 1}\\2^{10} &= 2^n\\n&=10\end{aligned}

Now that we all have the values that we need let’s go ahead and find the sum of the series.

\begin{aligned}S_n &=\dfrac{a_1(1 – r^n)}{1- r}\\&= \dfrac{2(1 – 2^{10})}{1- 2}\\&=\dfrac{2(1  -1024)}{-1}\\&=-2(-1023)\\&= 2046\end{aligned}

We’ll apply a similar process when finding the sum of $\dfrac{1}{27} + \dfrac{1}{9} + \dfrac{1}{3} + 1 + … + 81$. Let’s begin by determining the value of the common ratio, $r$.

\begin{aligned}r &= \dfrac{\dfrac{1}{9}}{\dfrac{1}{27}}\\&= 3\\r &= \dfrac{ \dfrac{1}{3}}{ \dfrac{1}{9}}\\&= 3\end{aligned}

We’ll now use the explicit rule to find the value of $n$ or the number of terms present in the finite geometric series.

\begin{aligned}81 &= \dfrac{1}{27}(3)^{n-1}\\3^{4} &= (3^{-3})3^{n – 1}\\3^{4} &= 3^{-3 + n – 1}\\3^4 &= 3^{n – 4}\\4 &= n – 4\\n&=8\end{aligned}

Now that we have all the values that we need, $a_1 = \dfrac{1}{27}$, $r = 3$, and $n = 8$, so let’s apply the formula for the sum.

\begin{aligned}S_n &=\dfrac{a_1 (1- r^n)}{1 – r}\\&=\dfrac{\dfrac{1}{27}(1- 3^8)}{1- 3}\\&= \dfrac{ \dfrac{1 – 3^8}{27}}{-2}\\&= -\dfrac{1}{2} \cdot \dfrac{6560}{27}\\&= \dfrac{3280}{27}\end{aligned}

Hence, we have the sum for the following geometric series.

a. $64 + 16 + 4 + 1 + … = \dfrac{256}{3}$
b. $-12 + -6 + -3 + -\dfrac{3}{2} + … = -24$
c. $2 + 4 + 8 + 16 + … + 1024 = 2046$
d. $\dfrac{1}{27} + \dfrac{1}{9} + \dfrac{1}{3} + 1 + … + 81 = \dfrac{3280}{27}$