Geometric Nets – Explanation & Examples

A polyhedron net is a shape where a non-overlapping edge joined polygons in the plane, re-arranged into another shape.

Albrecht Durer talked about nets in the book he wrote in 1525, named “A Course in the Art of Measurement with Compass and Ruler.” The arrangement of edges decides the shapes of the nets. A given net may be folded into a different convex polyhedron, depending upon the angles in which the edges are folded and which edges are joined together.

In this article, we will learn:

• What a geometric net is and a geometric net definition,
• We will also discuss using the geometric nets of different 3-D solids to find their surface area.

What is a Geometric Net?

A geometric net can be defined as a two-dimensional shape that can be modified to form a three-dimensional shape or a solid.

A net is defined as a pattern obtained when a three-dimensional figure is laid out flat, showing each face of the figure. A 3-D shape may have different nets.

Properties of 3D shapes

A three-dimensional geometric shape consists of the following parts:

• Faces – This is a curve or a flat surface on 3-D shapes
• Edges – An edge is a line segment between the faces.
• Vertices – A vertex is a point where the two edges meet.

For a geometric net to form a three-dimensional solid, the following conditions must be met:

• The geometric net and the 3-D shape should have the same number of faces.
• The shapes of the faces in the geometric net should match the corresponding shapes of the faces in the 3-D shape.

If the above two conditions are satisfied, visualize how the geometric net is to be folded to form the solid and make sure that all the sides fit together properly.

Let us have a look at the nets for different shapes.

A cuboid

A cuboid is a rectangular prism with; 6 rectangular faces, 12 edges, and 8 vertices. All the corner angles of a cuboid are 90 degrees.

• Net of a cuboid

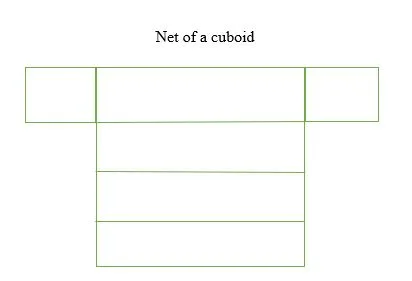
The surface area of a cuboid is given as:

SA = 2(lb + bh + lh)

A cube

By definition, a cube is a three-dimension figure with 6 equal square faces, 12 edges, and 8 vertices.

• Net of a cube

The surface area of a cube is equal to:

SA = 6a²

A cylinder

In geometry, a cylinder is a three-dimensional figure with two congruent circular bases connected with a curved surface. A cylinder has three faces, two edges, and zero vertices. The geometric net of a cylinder also consists of three faces, i.e., 2 circles and a rectangle.

• Net of a cylinder

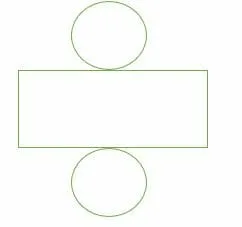
The surface area of a cylinder is given as:

SA = 2πr (h + r)

A cone

A cone is a geometrical shape with a circular base and a curved surface that tapers from the base to a point known as an apex or vertex. A cone has two faces, one edge, and a vertex.

• Net of a cone

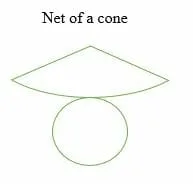
The surface area of a cone is given as:

SA = πr (r +√ (r² + h²) 

A Pyramid

A pyramid is a polyhedron whose base is any polygon, and the lateral faces are triangles. A square pyramid contains five faces, eight edges, and five vertices.

When a square pyramid is unfolded, its geometric net consists of a square base and 4 triangles.

• Net of A Square Pyramid

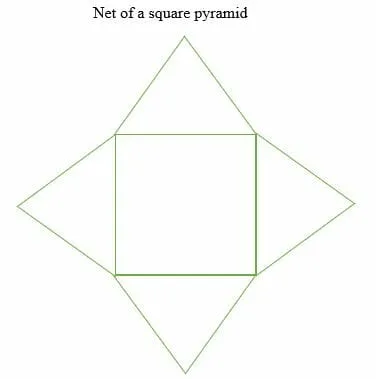
The surface area of any pyramid is given as:

SA = Base area + Lateral area

Let’s solve a few example problems involving the geometric nets of different solids.

Example 1

Find the cuboid’s surface area with a length of 12 m, a width of 4 m, and a height of 8 m.

Solution

The surface area of a cuboid is equal to the sum of all faces in a net of a cuboid.

= (8 x 4 + 12 x 8 + 12 x 4 + 12 x 8 + 12 x 4 + 8 x 4) m²

= (32 + 96 + 48 + 96 + 48 + 32) m²

= 352 m².

Example 2

Calculate the surface area of the net show below.

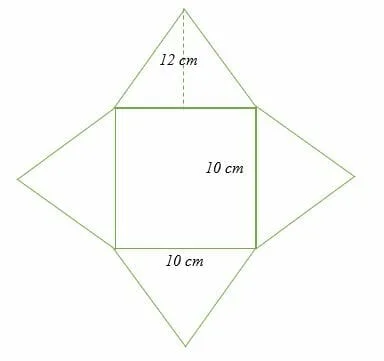
Solution

In the above net, the height, h = 12 cm, and the base is a square of the length, 10 cm.

The net’s total surface area is equal to the sum of the area of the square and the area of the four triangles.

Area of the square = a²

A = 10²

= 10 x 10

= 100 cm²

Area of the four triangles = 4 x ½ bh

= 4 x ½ x 12 x 10

= 240 m².

Total surface area of the net = 100 cm² + 240 m².

= 340 m².

Example 3

Calculate the surface area of the net shown below:

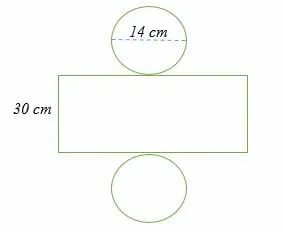
Solution

Surface area of the net = area of two circles + area of a rectangle.

Area of the two circles = 2 x 3.14 x 7 x 7

= 307.72 cm².

The length of the rectangle = circumference of the circle

= 3.14 x 14

= 43.96 cm

Area of the rectangle = 43.96 x 30

=1,318.8 cm²

Total surface area of the net = 307.72 + 1,318.8

= 1,626.52 cm².