Infinite series – Properties, Partial Sum, and Conditions

Infinite series results from us wanting to know how the sum of a series behaves when the terms are infinitely many. We can write any series we see in its infinite series form, so it’s no surprise that infinite series has physics, biology, and engineering.

Infinite series represents the successive sum of a sequence of an infinite number of terms that are related to each other based on a given pattern or relation.

Isn’t it amazing how, through the advancement of mathematics, it is now possible for us to predict the sum of a series made of an endless number of terms?

This article will discuss this series and show how we can predict different infinite series’ sum and partial sum. To make the most out of our discussion, make sure to review the following topics as well:

• We’ve discussed the common sequence and series in the past, including the arithmetic, geometric, and harmonic series.

• The properties of limits and the techniques in evaluating limits.

Why don’t we begin by understanding the components of infinite series?

What is an infinite series?                

As our introduction says, infinite series represents the sum of the infinite number of terms formed by a sequence. Below are examples of infinite series:

\begin{aligned}\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6} + \dfrac{1}{8} + \dfrac{1}{10} + … \end{aligned}

• This is an example of an infinite harmonic series, where the denominator increases by $2$ as the series increase.

  \begin{aligned}3 + 9 + 27 + 81 + 243 + … \end{aligned}

• This is an example of an infinite geometric series, where the next term is determined by multiplying $3$ to the previous term.

These examples give us an idea of what makes up an infinite series, so let’s go ahead and formally define infinite series. In the next section, we’ll learn how we can express them in terms of sigma notation.

Infinite series definition

Let’s say, we have a finite sequence that consists terms of $\{a_1, a_2, …, a_{n-1}, a_n\}$, so the sum of its finite series can be expressed as $a_1+a_2+ …+a_{n-1}+ a_n$.

The only difference for infinite series, the terms extend beyond $a_n$, so the infinite series will be of the form $a_1 + a_2 + a_3 + …$ or $\sum\limits_{n = 1}^{\infty} a_n$.

Let’s list some examples of finite and infinite series to understand better what makes infinite series unique.

These examples clearly demonstrates the main difference between an infinite series and finite series.

From these, we can clearly see that the only thing that stands infinite series out is that its terms are endless.

How to find the sum of an infinite series?                

At first, it may feel counter-intuitive to think that we can predict the sum of an infinite series. But thanks to limits and calculus, we’re able to create a systematic process to find the sum of a given infinite series.

But first, let’s take a look at this visual representation of an infinite geometric series.

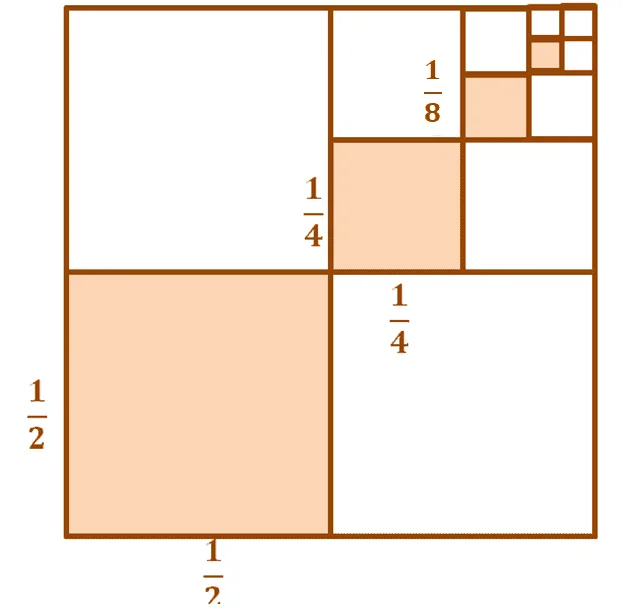
This is a good example of how we can find the sum of infinite series. That’s because as we continue to add more terms (so take half of the previous area), we’ll see that when combined altogether, the total area of the shaded region will fill up almost the entire square’s region.

Any guess on the sum of the infinite series,$\sum\limits_{n = 1}^{\infty} \dfrac{1}{2^n}$, then? Visually, since the regions will eventually make up the entire square, the sum of the infinite series is $1$.

But how do we confirm this mathematically? Before we dive right into the process of determining the sum of infinite series, let’s find out how to find the sum of a certain portion from a given infinite series.

How to find partial sum of infinite series?

The partial sum of an infinite series is simply the sum of a certain number of terms from the series. For example, the series $\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8}$ is simply a part of the infinite series, $\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + …$.

This means that the partial sum of the first three terms of the infinite series shown above is equal to $\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} = \dfrac{7}{8}$.

Here are some handy formulas that can be handy for you whenever you’re working with the partial sum of a given series.

In other words, we can use the properties we’ve learned about common finite series to find certain partial sums.

How to find the  infinite series’ sum based on its partial sum?

You might be wondering why we’re talking about partial sums when we’re supposedly dealing with the sums of infinite series. That’s because when we want to find the sum of an infinite series, we’ll need the expression of its partial sum.

Let’s say we have an infinite series, $\sum\limits_{i = 1}^{\infty} a_i = S$, so its partial sum for the first $n$ terms will be $\sum\limits_{i = 1}^{n}a S_n$.

• If the partial sum, $S_n$, converges, the infinite series, $S$, is expected to converge as well. In fact, $\lim{n \rightarrow \infty} S_n$ will represent the sum of the infinite series.

• If the partial sum, $S_n$, diverges, the infinite series, $S$, is expected to diverge as well. In fact, it will not be possible for us to predict the sum of the series when the partial sum diverges.

Why don’t we go ahead and observe the following geometric series and see what happens with their partial sum and infinite series’s sum?

Starting with the series, $\dfrac{1}{3} + \dfrac{1}{9} + \dfrac{1}{81} + …$, we can see that the common ratio is $\dfrac{1}{3}$ and the next terms will be smaller and will be approaching $0$.

The partial sum of the series of $n$ terms will be equal to $\dfrac{a(1 – r^n)}{1 – r}$, where $a = \dfrac{1}{3}$ and $r = \dfrac{1}{3}$.

\begin{aligned}S_n &= \dfrac{a(1 – r^n)}{1 – r}\\&= \dfrac{\dfrac{1}{3}\left(1 – \dfrac{1}{3}^n\right)}{1 – \dfrac{1}{3}}\\&=\dfrac{1}{2}\left( 1- \dfrac{1}{3}^n\right )\end{aligned}

Let’s take a look at the limit of $S_n$ as $n$ approaches infinity.

\begin{aligned}\lim_{x \rightarrow \infty} S_n &= \lim_{n \rightarrow \infty}\dfrac{1}{2}\left( 1- \dfrac{1}{3}^n\right )\\&= \dfrac{1}{2}- \dfrac{1}{2}\lim_{n \rightarrow \infty} \dfrac{1}{3}^n\\&= \dfrac{1}{2} – 0\\&= \dfrac{1}{2}\end{aligned}

Since the series converges to $\dfrac{1}{2}$, the sum of the series is equal to $\dfrac{1}{2}$.

What happens when the common ratio is greater than $1$? Let’s see how the series, $2 + 4 + 8 + 16 + …$ behaves to answer that question.

This times, we have $r = 2$ and $a = 2$.

\begin{aligned}S_n &= \dfrac{a(1 – r^n)}{1 – r}\\&= \dfrac{2\left(1 – 2^n\right)}{1 – 2}\\&=-2\left( 1- 2^n\right )\end{aligned}

Conceptually, we’re expecting the series to diverge, and that’s because as we add more terms, the partial sum drastically increases as well. We can confirm this guess by taking the limit of $S_n$ as it approaches infinity.

\begin{aligned}\lim_{n \rightarrow \infty} S_n &= \lim_{n \rightarrow \infty}2\left( 1- 2^n\right )\\&= 2- 2\lim_{n \rightarrow \infty} 2^n\\&= 2 – \infty\\&= \infty\end{aligned}

Since $\lim_{n \rightarrow \infty} S_n = \infty$, the infinite series’ diverges and will not have a fixed value.

Noticed how when the terms increase throughout the infinite series, the series diverges? That’s a helpful observation and something we need to keep in mind each time.

An important condition for the infinite series, $\sum\limits_{n = 1}^{\infty} a_n$, to be convergent, $\lim_{n \rightarrow \infty} a_n$ must be equal to $0$. This means that terms have to become smaller as the terms progress for the infinite series to be convergent.

Example 1

Write an expression for the $n$th term of the infinite series, $6 + 0.6 + 0.006 + …$ then answer the questions that follow.

    a. What are the next three terms of the series?

    b. What is the partial sum of the first six terms?
    c. Find the value of $\lim_{n \rightarrow \infty} S_n$, where $S_n$ represents the partial sum of the $n$th term of the series.

    d. Using the result from 1c, what is the sum of the infinite series?

Solution

Let’s take a look at the first three terms of $6 + 0.6 + 0.006 + …$.

• We can see that as the series progresses, the terms get smaller.

• To find the next three terms, we can move one more decimal place to the left each time.

a. Hence, the next three terms of the infinite series are $0.0006$, $0.00006$, and $0.000006$.

Now that we have all the six terms, we can simply add them up to find the partial sum of the first six terms of the series.

\begin{aligned}S_6 &= 6 + 0.6 + 0.06 + 0.006+ 0.0006+ 0.00006 + 0.000006\\ &= 6.666666\end{aligned}

b. The partial sum of the first six terms is $6.666666$.

When we move one decimal place to the left, we are simply dividing the previous term by $10$ to find the next term. We can confirm this by seeing the fraction form of the first six terms.

\begin{aligned}6\\0.6 &= \dfrac{6}{10}\\0.006 &= \dfrac{6}{100}\\0.0006 &= \dfrac{6}{1000}\\0.00006 &= \dfrac{6}{10000} \\0.000006 &= \dfrac{6}{100000}\\.\\.\\.\\a_n &= 6 \left(\dfrac{1}{10}^{n – 1}\right)\end{aligned}

This shows that the series is in fact an infinite geometric series, so we can express the sum of the $n$th terms as $\dfrac{a(1 – r^n)}{1 – r}$, where $a= 6$ and $r = \dfrac{1}{10}$.

\begin{aligned}S_n &= \dfrac{a(1 – r^n)}{1 – r}\\&= \dfrac{6\left(1 – \dfrac{1}{10}^n \right)}{1 – \dfrac{1}{10}}\\&= \dfrac{6\left(1 – \dfrac{1}{10}^n \right )}{\dfrac{9}{10}}\\&= \dfrac{20}{3}\left(1 – \dfrac{1}{10}^n \right )\end{aligned}

Now that we have the expression for $S_n$, we can execute $\lim_{n \rightarrow \infty} S_n$.

\begin{aligned}\lim_{n \rightarrow \infty} S_n&= \lim_{n \rightarrow \infty} \dfrac{20}{3}\left(1 – \dfrac{1}{10}^n \right )\\&= \dfrac{20}{3} – \dfrac{20}{3}\lim_{n \rightarrow \infty} \dfrac{1}{10}^n\\&=\dfrac{20}{3} – 0\\&=\dfrac{20}{3}\end{aligned}

c. Hence, $\lim_{n \rightarrow \infty} S_n = \dfrac{20}{3}$.

We can see that the partial sum limit as it approaches infinity is $\dfrac{20}{3}$. Also, the terms become smaller as the infinite series progress.

d. All this information will lead us to the fact that the series is indeed convergent.

Example 2

Write an expression for the $n$th term of the infinite series, $\dfrac{1}{2}+ \dfrac{1}{6} + \dfrac{1}{12}+ …$ then answer the questions that follow.

    a. What are the next three terms of the series?

    b. What is the partial sum of the first six terms?
    c. Find the value of $\lim_{n \rightarrow \infty} S_n$, where $S_n$ represents the partial sum of the $n$th term of the series.

    d. Using the result from 1c, what is the sum of the infinite series?

Solution

Let’s observe the series first using the three given terms.

\begin{aligned}\dfrac{1}{6} &= \dfrac{1}{2}\cdot \dfrac{1}{3}\\&= \dfrac{1}{2} \cdot \dfrac{1}{2 + 1} \\ \dfrac{1}{12} &= \dfrac{1}{3}\cdot \dfrac{1}{4}\\&= \dfrac{1}{3} \cdot \dfrac{1}{3 + 1}\end{aligned}

Using the observation that we have, to find the fourth term, we multiply $\dfrac{1}{4}$ and $\dfrac{1}{5}$. We’ll apply a similar process for the remaining terms that we need.

a. Hence, we have the following terms:

\begin{aligned}a_4 &= \dfrac{1}{4} \cdot \dfrac{1}{4 + 1} \\&= \dfrac{1}{20}\\a_5&= \dfrac{1}{5} \cdot \dfrac{1}{6}\\&= \dfrac{1}{30}\\a_6&= \dfrac{1}{6} \cdot \dfrac{1}{7}\\&= \dfrac{1}{42}\end{aligned}

b. Adding all the six terms will lead us to a partial sum of $\dfrac{6}{7}$ as shown below.

\begin{aligned}S_6 &= \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{12} + \dfrac{1}{20} + \dfrac{1}{30} + \dfrac{1}{42}\\&= \dfrac{6}{7}\end{aligned}

Notice something about the sum of the six terms? It’s simply equivalent to $1 – \dfrac{1}{7}$. Check out the sum for the first seven terms – you’ll get $1 – \dfrac{1}{8} = \dfrac{7}{8}$.

Why don’t we confirm this so that we can find $S_n$ in terms of $n$?

Observe that $\dfrac{1}{2} = 1- \dfrac{1}{2}$, $\dfrac{1}{6} = \dfrac{1}{2} – \dfrac{1}{3}$, $\dfrac{1}{12} = \dfrac{1}{3} – \dfrac{1}{4}$, and so on?

This means we can rewrite $S_n$ this way and see what happens.

\begin{aligned}S_n &= \dfrac{1}{2} + \dfrac{1}{6} + \dfrac{1}{12} + \dfrac{1}{20} + …\\&= \dfrac{1}{1 \times 2} + \dfrac{1}{2 \times 3} + \dfrac{1}{3 \times 4} + \dfrac{1}{4 \times 5} + … + \dfrac{1}{n(n + 1)}\\&=\left(1 – \dfrac{1}{2} \right ) + \left(\dfrac{1}{2} – \dfrac{1}{3} \right ) + \left(\dfrac{1}{3} – \dfrac{1}{4} \right ) + \left(\dfrac{1}{4} – \dfrac{1}{5} \right )+ … + \left( \dfrac{1}{n} – \dfrac{1}{n + 1}\right )\\&= 1 \cancel{- \dfrac{1}{2} +\dfrac{1}{2}} \cancel{- \dfrac{1}{3}+ \dfrac{1}{3}} \cancel{- \dfrac{1}{4} + \dfrac{1}{4}} … \cancel{-\dfrac{1}{n} +\dfrac{1}{n}} – \dfrac{1}{n + 1}\end{aligned}

This means that $S_n$ is simply equal to $1 – \dfrac{1}{n + 1} = \dfrac{n}{n + 1}$.

Now that we have the expression for $S_n$ in terms of $n$, we can find its limit as $n$ approaches infinity.

\begin{aligned}\lim_{x \rightarrow \infty} S_n &= \lim_{x \rightarrow \infty} \dfrac{n}{n + 1} \\lim_{x \rightarrow \infty} \dfrac{1}{1 + \dfrac{1}{n}} \\&= \dfrac{1}{1 + 0} \\&= 1\end{aligned}

c. This shows that $\lim_{x \rightarrow \infty} S_n = 1$.

This result makes sense since the difference between the numerator and denominator for all nth partial sums will always be $1$, so the sum must be close to $1$. We can also see that the next term is significantly smaller than the previous term.

d. From these observations, we can conclude that the series is, in fact, convergent.