Intersection of Line and Plane – Definition, Explanation, and Examples

Finding the intersection of line and plane highlights the relationship between the equations of the line and planes in a three-dimensional coordinate system. This also translates our understanding of intersections of equations in $\mathbb{R}^2$ to $\mathbb{R}^3$.The intersection of a line and a plane is a point that satisfies both equations of the line and a plane. It is also possible for the line to lie along the plane and when that happens, the line is parallel to the plane.This article will show you different types of situations where a line and a plane may intersect in the three-dimensional system. Since this extends our understanding of the equation of the line and the equation of the plane, it is important that you are familiar with the general forms of these two equations.By the end of the discussion, you’ll learn how to:

• Determine whether the line and the plane are parallel or intersect in one point.
• Use the parametric equations of the line and the scalar equation of the plane to find the intersection point of the two.
• Apply the concepts to solve the different problems involving the equations of a line and a plane.

Are you ready to begin? Let’s go ahead and see what happens when a line and a plane intersect in a space!

What Is the Intersection of a Line and a Plane?

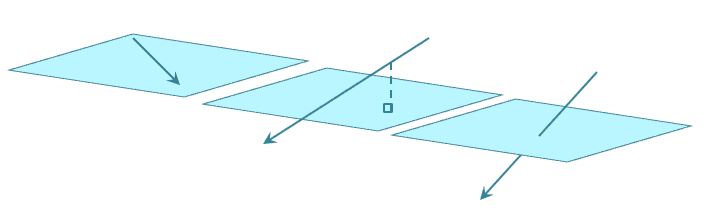
The intersection of a line and a plane is a point, $P(x_o, y_o, z_o)$, that satisfies the equation of the line and the plane in $\mathbb{R}^3$. However, when the line lies on the plane, there will be infinite possible intersections.In fact, there are three possibilities that may occur when a line and a plane interact with each other:

• The line lies within the plane, so the line and the plane will have infinite intersections.
• The line lies parallel to the plane, so the line and the plane will have no intersections.
• The line intersects the plane once, so the line and the plane will have one intersection.

Parallel Lines and PlanesWhen the normal vector,$\textbf{n}$, that is perpendicular to the plane, is also perpendicular to the directional vector, $\textbf{v}$, of the line, the line is parallel with the plane. We can confirm this by taking the dot product of the $\textbf{n}$ and $\textbf{v}$.\begin{aligned}\textbf{n} \cdot \textbf{v} &= 0\end{aligned}If the resulting dot product is zero, this confirms that the two vectors are perpendicular. When this happens, the line is parallel with the plane and will therefore have no intersection.Intersecting Lines and PlanesWhen a line and a plane intersects, we are guaranteed a common point shared by the two  This means that the parametric equations of the line, $\{x = x_o + at, y = y_o + bt, z = z_o + ct\}$, satisfies the scalar equation of the plane, $Ax + By + Cz +D = 0$.

\begin{aligned}\text{Plane} &: Ax + By + Cz + D = 0\\\text{Line} &: x= x_o + at,\phantom{x} y= y_o + bt, \phantom{x}z = z_o + ct\end{aligned}

\begin{aligned}A(x_o + at) + B(y+o + bt) + C(z_o + ct) +D &=0\end{aligned}

This shows that the parameter $t$ will be defined by the resulting equation shown above. The line and plane’s intersection points will be defined by the parameter and the equations of the line.

How To Find Where a Line Intersects a Plane?

Use the fundamental components to find the intersection point between a line and a plane. We’ve broken down the steps needed to find the point where the line passes through the plane.

• Write the equation of the line in its parametric form: $\{x = x_o + at, y = y_o + bt, z = z_o + ct \}$.
• Write the equation of the plane in its scalar form: $Ax + By + Cz + D =0$.
• Use $x$, $y$, and $z4’s corresponding parametric equations to rewrite the scalar equation of the plane.
• This leaves us with a single-variable equation, so we can now solve for $t$.
• Substitute $t$ back into the parametric equations to find the $x$, $y$, and $z$ components of the intersection.

Let’s try to find the intersection point formed by the line and plane with the following equations in parametric and scalar forms, respectively.\begin{aligned}2x + y &- 4z = 4\\\\x &= 1+ t\\y&= 4 + 2t\\ z&=t\end{aligned}The equation of the line is in their parametric forms and the equation of the plane is in scalar form. This means that we can use the parametric form of the line’s equation to rewrite the scalar equation of the plane.\begin{aligned}2x + y – 2z &= 4\\2(1+ t) + (4 + 2t) – 2(t) &= 4\end{aligned}Simplify the resulting expression then solve for the parameter, $t$.\begin{aligned}2+ 2t + 4 + 2t – 2t &= 4\\2t +6 &= 4\\2t&=-2\\ t&= -1\end{aligned}Use the parametric equations of the line and $t  = -1$ to find the components of the point.\begin{aligned}x &= 1+ (-1)\\&= 0\\y&= 4 + 2(-1)\\&=2\\ z&=-1\\\\(x, y,z) &= (0, 2, -1)\end{aligned}This means that the line and the plane will intersect at the point, $(0, 2, -1)$.Example 1Determine whether the line, $\mathbf{r} = (2, -3, 4) + t(2, -4, -2)$, intersects the plane, $ -3x -2y + z -4= 0$. If so, find their point of intersection.SolutionLet’s check if the line and the plane are parallel to each other. The equation of the line is in vector form, $\textbf{r} = \textbf{r}_o + \textbf{v}t. This means that the direction vector of the line is equal to:\begin{aligned}\textbf{v} = <2, -4, -2>.\end{aligned}Recall that we can use the coefficients before the variables of the plane equation in scalar form, $Ax + By + Cz + D = 0$, to find the normal vector. This means that the normal vector is as shown below.\begin{aligned}\textbf{n} = <-3, -2, 1>\end{aligned}Now, take the dot product of the direction vector and the normal vector. If the resulting dot product is zero, this will mean that the two vectors are perpendicular. Consequently, the line and the plane will be parallel.\begin{aligned}\textbf{v} \cdot \textbf{n}  &= <2, -4, 2>.\cdot <-3, -2, 1>\\&= 2(-3) + (-4)(-2) + 2(1)\\&= -6 + 8 + -2\\ &= 0\end{aligned}Since $\textbf{v} \cdot \textbf{n} = 0$, the given line and plane will be parallel.This shows that it can be helpful to check if the line and the plane are parallel to each other by quickly taking the dot product of the direction and normal vectors.Example 2Determine whether the line, $\mathbf{r} = (4, -1, 3) + t(1,  8, -2)$, intersects the plane, $ 2x – y + 3z – 15= 0$. If so, find their point of intersection.SolutionBy inspection, we can see that the direction vector is $\textbf{v} = <1, 8, -2>$ and the normal vector is $\textbf{n} = <2, -1, 3>$.\begin{aligned}\textbf{v} \cdot \textbf{n} &= <1, 8, -2> \cdot <2, -1, 3>\\&= 1(2) + 8(-1) + (-2)(3)\\&= 2 -8 -6\\ &= -12\end{aligned}This confirms that the line and the plane are not parallel, so let’s now see if they intersect each other. Rewrite the equation of the line so that we have the parametric form. We can do this by using %%EDITORCONTENT%%lt;a, b, c> = <1, 8, -2>$ and $(x_o, y_o, c_o) = (4, -1, 4)$ into the general form, $\{x = x_o + at, y = y_o + bt, z = z_o + ct\}$.\begin{aligned}x&= 4 + t\\ y&= -1 + 8t\\ z&= 4 – 2t\end{aligned}Use these expressions of $x$, $y$, and $z$, into the scalar equation of the plane to find $t$ as shown below.\begin{aligned}2(4 + t) – (-1 + 8t) + 3(4  -2t) – 15 &= 0\\8 + 2t +1 -8t + 12 -6t-15 &=0\\-12t&= -6\\t&= \dfrac{1}{2}\end{aligned}Now that we have the value of the parameter, $t = \dfrac{1}{2}$, use this to find the value of $x$, $y$, and $z$ from the parametric equations of the line.

\begin{aligned}x&= 4 + t\\ y&= -1 + 8t\\ z&= 4 – 2t\end{aligned}

\begin{aligned}x&= 4 + \dfrac{1}{2}\\&= \dfrac{9}{2}\\ y&= -1 + 8\cdot \dfrac{1}{2}\\&= 3\\ z&= 4 – 2 \cdot \dfrac{1}{2}\\&= 3\end{aligned}

These values represent the coordinates of the point of intersection shared between the line and the plane. We can double-check our answer by substituting these values back into the equation of the plane and see if the equation holds true.\begin{aligned}2x – y + 3z – 15 &= 0\\ 2\left(\dfrac{9}{2}\right ) – 3 + 3(3) – 15 &= 0\\0 &\overset{\checkmark}{=}0\end{aligned}This confirms that we got the correct intersection point. Hence, the given line and plane intersect at the point, $\left(\dfrac{9}{2}, 3, 3\right)$.Example 3Determine whether the line passing through the points $A = (1, -2, 13)$ and $B = (2, 0, -5)$, intersects the plane, $ 3x + 2y – z + 10 = 0$. If so, find their point of intersection.SolutionFirst, write down the equation of the line in parametric form. Since we’re given two points along the line, we can subtract these vectors to find a direction vector for the line.\begin{aligned}\textbf{v} &= <2-1, 0- -2, -5 -13>\\&= <1, 2, -18>\end{aligned}Using the first point, $A = (1, -2, 13)$, we can write the parametric form of the line as shown below.\begin{aligned}<a, b, c> &= \textbf{v}\\&= <1, 2, -18> \\ (x_o, y_o, z_o) &= A \\&= (1, -2, 13)\\\\x&=x_o + at\\&= 1 +t\\y&=y_o + bt\\&= -2 + 2t\\z&=z_o + ct\\&= 13 – 18t\end{aligned}Now that we have the parametric equations of the line, let’s use them to rewrite the equation of the plane.\begin{aligned}3x + 2y – z + 10 &= 0\\3(1 +t) + 2(-2 + 2t) – (13 – 18t) + 10 &= 0\\3 + 3t – 4 +4t -13 + 18t + 10 &=0 \\25t&= 4\\t&= \dfrac{4}{25}\\&= 0.16\end{aligned}Find the coordinates of the point of intersection by substituting the parameter, $t = 0.16$, into the equation.\begin{aligned}x&= 1 +t\\&= 1+ 0.16\\&=1.16\\y&= -2 + 2t\\&= -2 + 2(0.16)\\&= -1.68\\z&= 13 – 18t\\&= 13 – 18(0.16)\\&= 10.12 \end{aligned}We can also double-check our answer by substituting the values into the equation of the plane.\begin{aligned}3x + 2y – z + 10 &= 0\\ 3(1.16) + 2(-1.68) -10.12 + 10&= 0\\0 &\overset{\checkmark}{=}0\end{aligned}This means that the line and the plane intersect at the point, $(1.16, -1.68, 10.12)$.Example 4Determine whether the line, $\mathbf{r} = (1, -1, 2) + t(2, -4, -2)$, intersects the plane that contains the points, $(1, 2, -3)$, $(2, 3, 1)$, and $(0, -2, -1)$ . If so, find their point of intersection.SolutionUse the three points to find the normal vector of the plane. If we let $A = (1, 2, -3)$, $B =(2, 3, 1)$, and $C = (0, -2, -1)$, the normal vector is simply the cross-product of cross product of $\overrightarrow{AB}$ and $\overrightarrow{BC}$.Find the vector components of $\overrightarrow{AB}$ and $\overrightarrow{BC}$ by subtracting their components as shown below.

\begin{aligned}\boldsymbol{\overrightarrow{AB}}\end{aligned}	\begin{aligned}\overrightarrow{AB} &= B – A \\&= <2 -1, 3 – 2, 2 – -3>\\&= <1, -1, 5>\end{aligned}
\begin{aligned}\boldsymbol{\overrightarrow{AC}}\end{aligned}	\begin{aligned}\overrightarrow{AC} &= C -A \\&= <0 -1, -2 – 2, -1 – -3>\\&= <-1, -4, 2>\end{aligned}

Evaluate their cross product to find the normal vector.\begin{aligned}\textbf{n} &= \overrightarrow{AB} \times \overrightarrow{AC} \\&= \begin{vmatrix}\textbf{i} &\textbf{j}  &\textbf{k} \\2 &3  &4 \\-1 &1  &2\end{vmatrix}\\&= [-1\cdot 2-5\left(-4\right)]\textbf{i} + [5\left(-1\right)-1\cdot 2]\textbf{j} + [1\cdot \left(-4\right)-\left(-1\cdot \left(-1\right)\right)]\textbf{k}\\&= 18\textbf{i} – 7\textbf{j} – 5\textbf{k}\\&= <18, -7, -5>\end{aligned}Using the point, $A = (1, 2, -3)$, and the normal vector, %%EDITORCONTENT%%lt;18, -7, -5>$, we can now write down the equation of the plane as shown below.\begin{aligned}(x_o, y_o, z_o) &= (1, 2, -3)\\ <a, b, c> &= <18, -7, -5>\\\\ a(x –x_o) + b(y – y_o) + c(z – z_o) &= 0\\18(x –  1)  -7(y – 2) -5(z + 3) &= 0\end{aligned}Rearrange this equation into the form, $Ax + By + Cz + D =0$, we have\begin{aligned}18x –  18  -7y + 14 -5z – 15 &= 0\\18x – 7y – 5z + 18 – 14 +15&= 0\\18x – 7y – 5z + 19&=0\end{aligned}We can also use the normal vector, $\textbf{n} = <18, -7, -5>$, and the direction vector, $\textbf{v} = <2, -4, -2>$, to rule out the chance that the line and the plane are parallel.\begin{aligned}\textbf{v} \cdot \textbf{n}  &= <2, -4, 2>.\cdot <18, -7, -5>\\&= 2(18) + (-4)(-7) + 2(-5)\\&= 36 + 28 + -10\\ &= 54\end{aligned}Since the cross product is not equal to zero, we are guaranteed that the line and plane would intersect.Using the equation, $18x – 7y – 5z + 19 =0$, and the parametric form of $\mathbf{r} = (1, -1, 2) + t(2, -4, -2)$, find the value of $t$ as shown below.\begin{aligned}x &= 1 + 2t \\ y &= -1 – 4t\\ z&= 2 – 2t\end{aligned}\begin{aligned}18x – 7y – 5z + 19 &=0\\18(1 + 2t) – 7(-1- 4t) – 5(2 – 2t) + 19 &= 0\\ 18 + 36t + 7 + 28t – 10 + 10t + 19 &= 0\\74t &= -34\\t&= – \dfrac{17}{37}\end{aligned}Now that we know the value of the parameter, $t = -\dfrac{17}{37}$, we can find the coordinates of intersection by substituting $t = -\dfrac{17}{37}$ into the parametric equations.\begin{aligned}x &= 1 + 2\left(-\dfrac{17}{37} \right )\\&= \dfrac{3}{37} \\ y &= -1 – 4\left(-\dfrac{17}{37} \right )\\&= \dfrac{31}{37}\\ z&= 2 – 2\left(-\dfrac{17}{37} \right ) \\&= \dfrac{108}{37}\end{aligned}This means that the line and the point intersects at $\left(\dfrac{3}{37}, \dfrac{31}{37}, \dfrac{108}{37}\right)$.

Practice Questions

1. Determine whether the line, $\mathbf{r} = (1, 0, -1) + t(-2, 3, 0)$, intersects the plane, $ 2x – 3y + z – 14= 0$. If so, find their point of intersection.2. Determine whether the line, $\mathbf{r} = (1, -2, 1) + t(-3, 3, 3)$, intersects the plane, $ -5x +4y – z + 4= 0$. If so, find their point of intersection. 3. Determine whether the line passing through the points $A = (4, -5, 6)$ and $B = (3, 0, 8)$, intersects the plane, $ 2x + 3y – 4z – 20 = 0$. If so, find their point of intersection.

Answer Key

1. The line and the plane will intersect at $(3, -3, -1)$. 2. The line and the plane are parallel. 3. The line and the plane will intersect at $(-6.2, 46, 26.4)$.