Inverse of a Function – Explanation & Examples

What is an inverse function?

In mathematics, an inverse function is a function that undoes the action of another function.

For example, addition and multiplication are the inverse of subtraction and division, respectively.

The inverse of a function can be viewed as reflecting the original function over the line y = x. In simple words, the inverse function is obtained by swapping the (x, y) of the original function to (y, x).

We use the symbol f ^{− 1} to denote an inverse function. For example, if f (x) and g (x) are inverses of each other, then we can symbolically represent this statement as:

g(x) = f ^{− 1}(x) or f(x) = g⁻¹(x)

One thing to note about the inverse function is that the inverse of a function is not the same as its reciprocal, i.e., f ^{– 1} (x) ≠ 1/ f(x). This article will discuss how to find the inverse of a function.

Since not all functions have an inverse, it is therefore important to check whether a function has an inverse before embarking on determining its inverse.

We check whether or not a function has an inverse in order to avoid wasting time trying to find something that does not exist.

One-to-one functions

So how do we prove that a given function has an inverse? Functions that have inverse are called one-to-one functions.

A function is said to be one-to-one if, for each number y in the range of f, there is exactly one number x in the domain of f such that f (x) = y.

In other words, the domain and range of one-to-one function have the following relations:

• Domain of f⁻¹ = Range of f.

•  Range of f⁻¹ = Domain of f.

For example, to check if f(x) = 3x + 5 is one to one function given, f(a) = 3a + 5 and f(b) = 3b + 5.

⟹ 3a + 5 = 3b + 5

⟹ 3a = 3b

⟹ a = b.

Therefore, f (x) is one-to-one function because, a = b.

Consider another case where a function f is given by f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. This function is one-to-one because none of its y -­ values appear more than once.

What about this other function h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Function h is not one-to-one because the y­- value of –9 appears more than once.

You can also graphically check one-to-one function by drawing a vertical line and horizontal line through a function graph. A function is one-to-one if both the horizontal and vertical line passes through the graph once.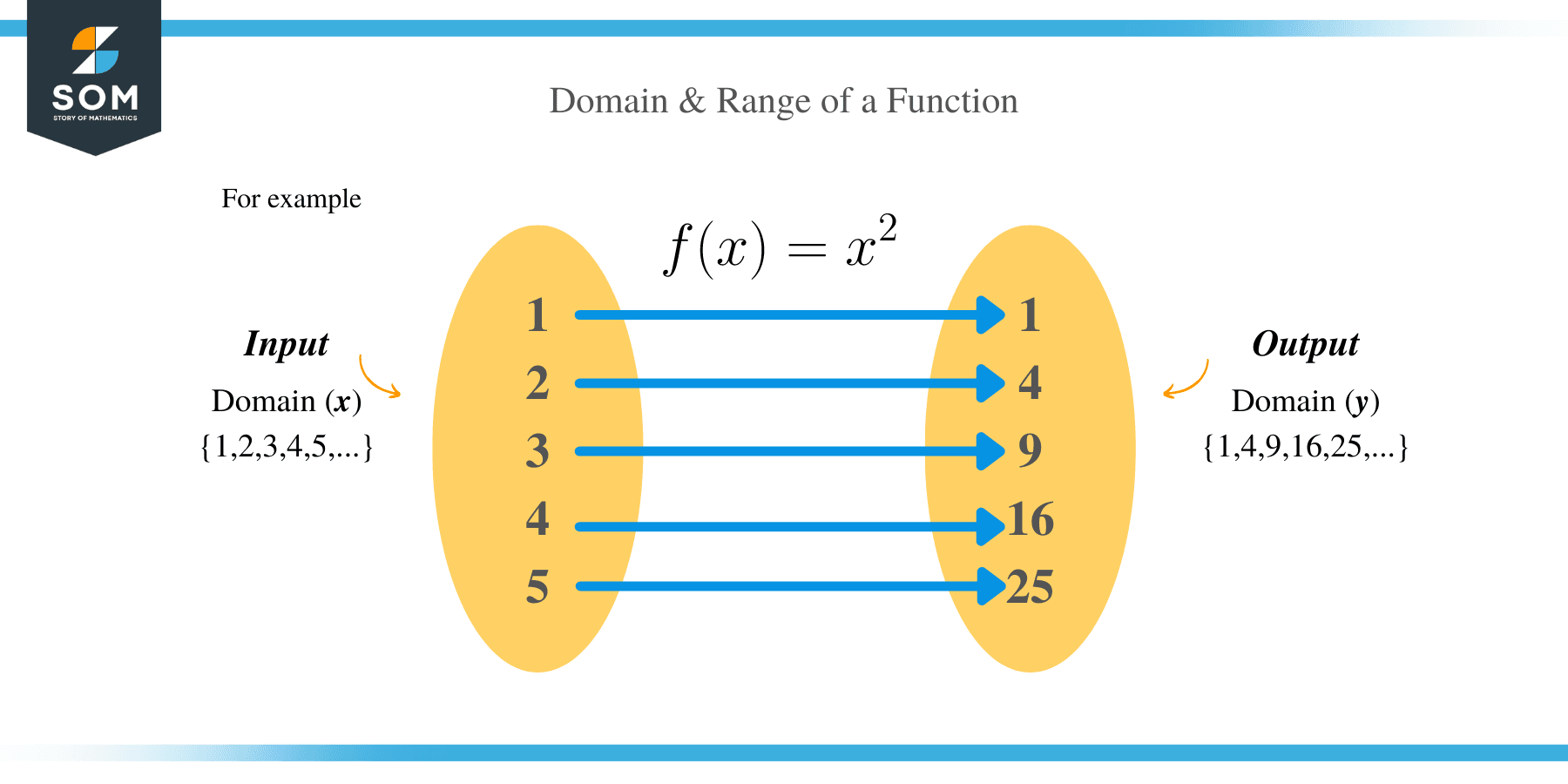

How to Find the Inverse of a Function?

Finding the inverse of a function is a straightforward process, though we really need to be careful with a couple of steps. In this article, we are going to assume that all functions we are going to deal with are one to one.

Here is the procedure of finding of the inverse of a function f(x):

• Replace the function notation f(x) with y.
• Swap x with y and vice versa.
• From step 2, solve the equation for y. Be careful with this step.
• Finally, change y to f⁻¹(x). This is the inverse of the function.
• You can verify your answer by checking if the following two statements are true:

⟹ (f ∘ f⁻¹) (x) = x

⟹ (f⁻¹ ∘ f) (x) = x

Let’s work a couple of examples.

Example 1

Given the function f (x) = 3x − 2, find its inverse.

Solution

f(x) = 3x − 2

Replace f(x) with y.

⟹ y = 3x − 2

Swap x with y

⟹ x = 3y − 2

Solve for y

x + 2 = 3y

Divide through by 3 to get;

1/3(x + 2) = y

x/3 + 2/3 = y

Finally, replace y with f⁻¹(x).

f⁻¹(x) = x/3 + 2/3

Verify (f ∘ f⁻¹) (x) = x

(f ∘ f⁻¹) (x) = f [f ⁻¹ (x)]

= f (x/3 + 2/3)

⟹ 3(x/3 + 2/3) – 2

⟹ x + 2 – 2

= x

Hence, f ⁻¹ (x) = x/3 + 2/3 is the correct answer.

Example 2

Given f(x) = 2x + 3, find f⁻¹(x).

Solution

f(x) = y = 2x + 3

2x + 3 = y

Swap x and y

⟹2y + 3 = x

Now solve for y

⟹2y = x – 3

⟹ y = x/2 – 3/2

Finally substitute y with f ⁻¹(x)

⟹ f ⁻¹ (x) = (x– 3)/2

Example 3

Give the function f (x) = log₁₀ (x), find f ⁻¹ (x).

Solution

f (x) = log₁₀ (x)

Replaced f (x) with y

⟹ y = log₁₀ (x) ⟹ 10 ^y = x

Now swap x with y to get;

⟹ y = 10 ^x

Finally, substitute y with f⁻¹(x).

f ^-1 (x) = 10 ^x

Therefore, the inverse of f(x) = log₁₀(x) is f^-1(x) = 10^x

Example 4

Find the inverse of the following function g(x) = (x + 4)/ (2x -5)

Solution

g(x) = (x + 4)/ (2x -5) ⟹ y = (x + 4)/ (2x -5)

Interchange y with x and vice versa

y = (x + 4)/ (2x -5) ⟹ x = (y + 4)/ (2y -5)

⟹ x(2y−5) = y + 4

⟹ 2xy − 5x = y + 4

⟹ 2xy – y = 4 + 5x

⟹ (2x − 1) y = 4 + 5x

Divide both side of the equation by (2x − 1).

⟹ y = (4 + 5x)/ (2x − 1)

Replace y with g ^{– 1}(x)

= g ^{– 1}(x) = (4 + 5x)/ (2x − 1)

Proof:

(g ∘ g⁻¹) (x) = g [g ⁻¹(x)]

= g [(4 + 5x)/ (2x − 1)]

= [(4 + 5x)/ (2x − 1) + 4]/ [2(4 + 5x)/ (2x − 1) − 5]

Multiply the both the numerator and denominator by (2x − 1).

⟹ (2x − 1) [(4 + 5x)/ (2x − 1) + 4]/ [2(4 + 5x)/ (2x − 1) − 5] (2x − 1).

⟹ [4 + 5x + 4(2x − 1)]/ [ 2(4 + 5x) − 5(2x − 1)]

⟹ [4 + 5x + 8x−4]/ [8 + 10x − 10x + 5]

⟹13x/13 = x
Therefore, g ^{– 1} (x) = (4 + 5x)/ (2x − 1)

Example 5

Determine the inverse of the following function f(x) = 2x – 5

Solution

Replace f(x) with y.

f(x) = 2x – 5⟹ y = 2x – 5

Switch x and y to get;

⟹ x = 2y – 5

Isolate the variable y.

2y = x + 5

⟹ y = x/2 + 5/2

Change y back to f ^–1(x).

⟹ f ^–1(x) = (x + 5)/2

Example 6

Find the inverse of the function h(x) = (x – 2)³.

Solution

Change h (x) to y to get;

h(x) = (x – 2)³⟹ y = (x – 2)³

Swap x and y

⟹ x = (y – 2)³

Isolate y.

y³ = x + 2³

Find the cube root of both sides of the equation.

³√y³ = ³√x³ + ³√2³

y = ³√ (2³) + 2

Replace y with h ^{– 1}(x)

h ^{– 1}(x) = ³√ (2³) + 2

Example 7

Find the inverse of h (x) = (4x + 3)/(2x + 5)

Solution

Replace h (x) with y.

h (x) = (4x+3)/(2x+5) ⟹ y = (4x + 3)/(2x + 5)

Swap x and y.

⟹ x = (4y + 3)/ (2y + 5).

Solve for y in the above equation as follows:

⟹ x = (4y + 3)/ (2y + 5)

Multiply both sides by (2y + 5)

⟹ x (2y + 5) = 4y + 3

Distribute the x

⟹ 2xy + 5x = 4y + 3

Isolate y.

⟹ 2xy – 4y = 3 – 5x

⟹ y (2x – 4) = 3 – 5x

Divide through by 2x – 4 to get;

⟹ y = (3 – 5x)/ (2x – 4)

Finally replace y with h ^{– 1}(x).

⟹ h ^{– 1} (x) = (3 – 5x)/ (2x – 4)