Iterated Integral – Definition, Formula, and Examples

Through the iterated integral, we can now extend the fundamental theorem of calculus for definite integrals with two or more variables. Knowing how to evaluate iterated integrals is important if we want to master our understanding of double and triple integrals.

The iterated integral allows us to integrate multivariable functions. Similar to partial derivatives, we take succeeding partial integrals one variable at a time.

Our discussion will focus on the definition of iterated integrals and their components. We’ll also show you the process of evaluating iterated integrals here, so knowledge of integral properties and formulas are assumed throughout this article. Take a quick refresher on integration techniques we’ve learned in the past in case you need them.

For now, let’s understand the components that makeup iterated integrals!

What Is an Iterated Integral?

An iterated integral occurs when we want to integrate a multivariable function such as $f(x, y)$ and $f(x, y, z)$. Through iterated integrals, we can evaluate these functions by taking the integrals of the function consecutively and with respect to one variable each time.

\begin{aligned}\int_{c}^{d} \int_{a}^{b} f(x, y) &\phantom{x}dxdy \\ \int_{e}^{f} \int_{c}^{d} \int_{a}^{b} f(x, y, z) &\phantom{x}dxdydz \end{aligned}

These two integrals are two of the most known examples of iterated integrals – the double integral and the triple integral. Thanks to iterated integration, we can easily evaluate these types of integrals. Throughout our discussion, we’ll use double integrals as examples – starting by breaking down the definition of double integrals as iterated integrals.

Iterated Integral Definition

Suppose that $f(x, y)$ is a continuous function within its rectangular domain, $R = [a, b] \times [c, d]$.  By Fubini’s theorem, we can define the double integral of $f(x, y)$ with respect to $dx$ and $dy$ as the iterated integral shown below.

\begin{aligned}\int\int_{R} f(x, y) \phantom{x}dA &= \int_{a}^{b} \int_{c}^{d} f(x, y) \phantom{x}dy dx \\&=\int_{c}^{d} \int_{a}^{b} f(x, y) \phantom{x}dx dy\end{aligned}

The number of single integrals represents the number of times we’ll integrate the given function. This means that for double integral, we’ll integrate the function twice in a row. For triple integral, we’ll have to integrate the function three times in a row.

 The two forms highlight the importance of iterated integrals: we evaluate them with respect to one variable first by treating the other variables as constant. We repeat the process until we have completely evaluated the iterated integral that we’re given.

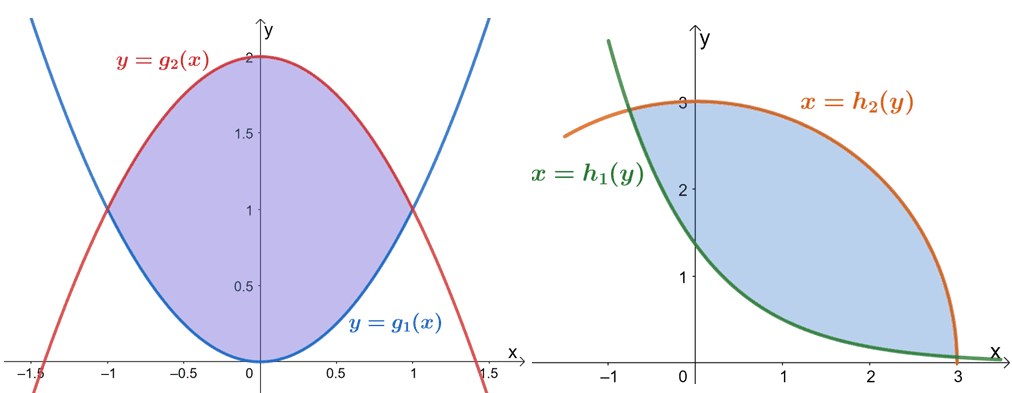
There are instances when it’s easier to start with the function that is in terms of $x$ or functions defined by $y$. The image above represents these two cases for double integrals when the regions we’re working on are not defined by a rectangular region. Here are two ways we can write the double integral as iterated integral.

\begin{aligned}\textbf{Case 1:}\phantom{xxxxxx}\\R = \{(x, y)| a &\leq x \leq b, g_1(x) \leq y \leq g_2(x)\}\\\int \int_R f(x, y) \phantom{x}dA &=\int_{a}^{b} \int_{g_1(x)}^{g_2(x)} f(x, y) dy\phantom{x} dx\\\\\textbf{Case 2:}\phantom{xxxxxx}\\R =\{(x, y)| h_1&(y) \leq x \leq h_2(y), c \leq y \leq d\}\\\int \int_R f(x, y) \phantom{x}dA &=\int_{c}^{d} \int_{h_1(y)}^{h_2(y)} f(x, y) dx\phantom{x} dy\end{aligned}

Now that we’ve covered all the fundamentals we need to establish iterated integrals, let’s dive right into understanding how we can evaluate integrals like this. Most of our examples will cover double integrals, so in case you want to explore iterated integrals with three variables, head over to our article on triple integral right after.

How To Calculate Iterated Integral?       

We can calculate iterated integrals by integrating with respect to one variable first. Just like partial derivatives, we start with the innermost layer and “partially integrate” the function with respect to the innermost variable.

Let us break down the steps for you when calculated iterated integrals over a rectangular region, $R = [a, b] \times [c, d]$.

For example, if we want to evaluate the iterated integral, $\int_{0}^{2} \int_{0}^{2} 4x^2y^3 \phantom{x}dx dy$, we begin by integrating $4x^2y^3$ with respect to $x$ first from $x = 0$ to $x = 2$.

\begin{aligned}\int_{0}^{2}\int_{0}^{2} 4x^2y^3 \phantom{x}dxdy&= \int_{0}^{2}\left[{\color{Teal}\int_{0}^{2} 4x^2y^3 \phantom{x}dx}\right ] dy\\&= \int_{0}^{2}\left[ 4y^3{\color{Teal}\int_{0}^{2} x^2} \phantom{x}{\color{Teal}dx}\right ]dy\\&= \int_{0}^{2}4y^3{\color{Teal}\left[\left(\dfrac{x^3}{3}\right) \right ]_{0}^{2}} \phantom{x}dy\\&= \int_{0}^{2} 4y^3 \left(\dfrac{2^3}{3} – \dfrac{0^3}{3} \right ) \phantom{x}dy\\&= \int_{0}^{2} \dfrac{32}{3}y^3\end{aligned}

We’re now left with a definite integral in one variable, so we can integrate our resulting expression with respect to $y$.

\begin{aligned}\int_{0}^{2}\int_{0}^{2} 4x^2y^3 \phantom{x}dxdy&= \dfrac{32}{3}\int_{0}^{2} y^3 \phantom{x}dy\\&= \dfrac{32}{3} \left[\dfrac{y^4}{4} \right ]_{0}^{2}\\&= \dfrac{32}{3}\left[\dfrac{2^4}{4} – \dfrac{0^4}{4} \right ]\\&= \dfrac{128}{3}\end{aligned}

This means that when evaluated, $\int_{0}^{2} \int_{0}^{2} 4x^2y^3 \phantom{x}dx dy$ is equal to $\dfrac{128}{3}$. Switching the order of the integrals will return the same value.

\begin{aligned}\int_{0}^{2}\int_{0}^{2} 4x^2y^3 \phantom{x}dxdy&= \int_{0}^{2}\left[{\color{DarkOrange}\int_{0}^{2} 4x^2y^3 \phantom{x}dx}\right ] dy\\&= \int_{0}^{2}\left[ 4x^2{\color{DarkOrange}\int_{0}^{2} y^3} \phantom{x}{\color{DarkOrange}dy}\right ]dx\\&= \int_{0}^{2}4x^2{\color{DarkOrange}\left[\left(\dfrac{y^4}{4}\right) \right ]_{0}^{2}} \phantom{x}dy\\&= \int_{0}^{2} 4x^2 \left(\dfrac{2^4}{4} – \dfrac{0^4}{4} \right ) \phantom{x}dy\\&= \int_{0}^{2} 16x^2 \phantom{x}dy\\&= 16\left[\dfrac{x^3}{3} \right ]_0^{2}\\&= \dfrac{128}{3}\end{aligned}

We’ll apply a similar approach when evaluating iterated integrals bounded by irregular regions. When bounded by the region, $R = [h_1(y), h_2(y)] \times [c, d]$, we integrate the expression with respect to $x$ first and evaluate the expression from $x = h_1(y)$ to $x = h_2(y)$. Once we have a function in terms of $y$, we integrate the expression with respect to $y$.

\begin{aligned}\int_{c}^{d} \overbrace{\left[{\color{DarkOrange}\int_{h_1(y)}^{h_2(y)} f(x, y) \phantom{x}dx} \right ]}^{\displaystyle{\color{DarkOrange}\text{function in terms of }y}} dy\end{aligned}

 Similarly, if we’re working with an iterated integral bounded by the region, $R = [a, b] \times [g_1(x), g_2(x)]$, we first integrate the function with respect to $y$ then $x$.

For example, if we want to evaluate the iterated integral, $\int_{1}^{2} \int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dx dy$, we integrate the function with respect to $x$ and treating $y$ as a constant.

\begin{aligned}\int_{1}^{2} \int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dxdy &=  \int_{1}^{2} \left[{\color{Teal}\int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dx} \right ]dy\end{aligned}

 Apply u-substitution to integrate the $\int e^{\displaystyle{x/y}} \phantom{x}dx$ as shown below.

\begin{aligned} u = \dfrac{x}{y} &\Rightarrow du = \dfrac{1}{y} \phantom{x}dx\\\int e^{\displaystyle{x/y}} \phantom{x}dx&= y\int e^u \phantom{x}du\\&= ye^{\displaystyle{u}}\\ &=ye^{\displaystyle{x/y}}\end{aligned}

Now, let’s go back to iterated expression and use this result to simplify the inner integral.

\begin{aligned}\int_{1}^{2} \int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dxdy &=  \int_{1}^{2} \left[{\color{Teal}\int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dx} \right ] \phantom{x}dy\\&= \int_{1}^{2} \left[{\color{Teal} ye^{\displaystyle{x/y}}} \right ]_{y}^{y^2}\phantom{x}dy\\&= \int_{1}^{2}\left(ye^{\displaystyle{y^2/y}} – ye^{\displaystyle{y/y}} \right)\phantom{x}dy\\&= \int_{1}^{2} (ye^{\displaystyle{y}} – ye) \phantom{x}dy\end{aligned}

We have a single integral now, so let’s integrate the resulting expression with respect to $y$ this time.

\begin{aligned}\int_{1}^{2} \int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dxdy &= \int_{1}^{2} (ye^{\displaystyle{y}} – ye) \phantom{x}dy\\&= [ye^{\displaystyle{y}}]_{1}^{2} –  \int_{1}^{2}e^{\displaystyle{y}} \phantom{x}dy – \int_{1}^{2} ye\phantom{x}dy\\&= \left[ye^{\displaystyle{y}} – e^{{\displaystyle{y}}} + \dfrac{1}{2}ey^2\right]_1^2\\&= \left[\left(2e^2 – e^2 + \dfrac{1}{2}e \cdot 2^2 \right ) – \left(1e^1 – e^1 + \dfrac{1}{2}e \cdot 1^2 \right ) \right ]\\&= e^2 – \dfrac{3}{2}e\\&\approx 3.31\end{aligned}

This means that $\int_{1}^{2} \int_{y}^{y^2} e^{\displaystyle{x/y}} \phantom{x}dx dy$ is equal to $e^2 – \dfrac{3}{2}e$ or approximately equal to $3.31$. We’ve shown you two examples on how one can evaluate iterated integrals, so it’s now time for you to master this topic by working on more problems involving iterated integrals!

Example 1

Calculate the double integral, $\int \int_R (2x – 3y^2) \phantom{x}dA$,  over the rectangular region, $R = [2, 6] \times [1, 2]$.

Solution

From the bounds of $R$, we want to integrate the function, $(2x – 3y^2)$, from $x = 2$ to $y = 6$ and from $y = 1$ to $y = 2$. As we have shown in our earlier discussion, the order of integration will return the same value. We’ll set up the iterated integral so that we integrate the iterated integral with respect to $x$ first.

\begin{aligned}\int \int_R (2x -3y^2) \phantom{x}dA &= \int_{1}^{2} \int_{2}^{6} (2x – ey^2) \phantom{x}dxdy \end{aligned}

Treat $y$ as a constant for now and evaluate the function with respect to $x$ as shown below.

\begin{aligned}\int_{1}^{2}\left[{\color{Teal} \int_{2}^{6} (2x – ey^2) \phantom{x}dx} \right ]dy &= \int_{1}^{2} \left[{\color{Teal} 2 \cdot \dfrac{x^2}{2} – ey^2x}\right ]_{1}^{2} \phantom{x}dy\\&= \int_{1}^{2} \left[x^2 – ey^2x \right ]_{1}^{2} \phantom{x}dy\\&= \int_{1}^{2} [(2^2 – 2ey^2) – (1^2 – 1ey^2)] \phantom{x}dy\\&= \int_{1}^{2} (3 – ey^2)\phantom{x}dy\end{aligned}

Now, evaluate the iterated integral with respect to its remaining variable, $y$.

\begin{aligned}\int_{1}^{2} (3 – ey^2)\phantom{x}dy &= \int_{1}^{2} 3 \phantom{x}dy – \int_{1}^{2} ey^2 \phantom{x}dy\\&= [3y]_{1}^{2} – \left[\dfrac{ey^3}{3} \right ]_{1}^{2}\\&= [3(2) – 3(1)] – \left[\dfrac{e(2^3)}{3} – \dfrac{e(1^3)}{3}\right]\\&=3 – \dfrac{7e^3}{3}\\&= -43.867\end{aligned}

This shows that $\int \int_R (2x – 3y^2) \phantom{x}dA$, where $R = [2, 6] \times [1, 2]$, is equal to $3 – \dfrac{7e^3}{3}$ or approximately equal to $-43.867$.

Example 2

Calculate the iterated integral, $\int \int_R 4x^2y^3 \phantom{x}dA$, over the rectangular region, $R = [y, y^2] \times [0, 1]$.

Solution

Evaluate the iterated integral with the following limits: from $x = y$ to $x = y^2$ and from $y = 0$ to $y = 1$.

\begin{aligned}\int \int_R \dfrac{x}{\ln x} \phantom{x}dA &= \int_{0}^{1} \int_{y}^{y^2} 4x^2y^3 \phantom{x}dxdy \end{aligned}

As with our previous examples, let’s integrate the function with respect to $x$ first and treat $y$ as a constant.

\begin{aligned}\int_{0}^{1} \left[{\color{Teal}\int_{y}^{y^2} 4x^2y^3\phantom{x}dx} \right ]dy &= \int_{0}^{1} \left[4y^3{\color{Teal}\int_{y}^{y^2} x^2\phantom{x}dx} \right ]dy\\&= \int_{0}^{1} 4y^3\left[\dfrac{x^3}{3} \right ]_{y}^{y^2} \phantom{x}dy\\&= \int_{0}^{1} \dfrac{4y^3}{3} [(y^2)^3 – (y)^3] \phantom{x}dy \\&= \int_{0}^{1} \dfrac{4y^3}{3}(y^6 – y^3) \phantom{x}dy\end{aligned}

Now, integrate the resulting expression with respect to $y$ to find the value of the iterated integral as shown below.

\begin{aligned}\int_{0}^{1} \dfrac{4y^3}{3}(y^6 – y^3) \phantom{x}dy &= \dfrac{4}{3}\int_{0}^{1} (y^9 – y^6) \phantom{x}dy\\&= \dfrac{4}{3}\left[\dfrac{y^{10}}{10} – \dfrac{y^7}{7} \right ]_0^1\\&= \dfrac{4}{3}\left[\left( \dfrac{1^{10}}{10} – \dfrac{1^7}{7}\right ) – \dfrac{0^{10}}{10} – \dfrac{0^7}{7}\right ] \\&= \dfrac{4}{3}\left(-\dfrac{3}{70} \right )\\&= -\dfrac{2}{35}\\ &\approx -0.057\end{aligned}

This means that the iterated integral is equal to $-\dfrac{2}{35}$ or approximately equal to $-0.057$.

Example 3

Calculate the iterated integral, $\int \int_R xe^{xy} \phantom{x}dA$, over the rectangular region, $R = [0, 1] \times [0, \ln 4]$.

Solution

There are two ways we can write the iterated integral: with $dx$ as the inner integral and $dy$ as the inner integral instead.

\begin{aligned}\int \int_R xe^{xy} \phantom{x}dA  &= \int_{0}^{\ln 4} \int_{0}^{1} xe^{xy} \phantom{x}dxdy\\ &= \int_{0}^{1} \int_{0}^{\ln 4} xe^{xy} \phantom{x}dydx\end{aligned}

Why do we show you the two forms? That’s because it’s important to show you an example where one form is a better option. We’ll have to use integration by parts if we integrate with respect to $x$ while the u-substitution method will be enough if we integrate with respect to $y$. Hence, integrating with respect to $y$ will save us more time.

\begin{aligned}\int_{0}^{1}\left[{\color{DarkOrange} \int_{0}^{\ln 4} xe^{xy} \phantom{x}dy} \right ]dx &= \int_{0}^{1} \left[x {\color{DarkOrange} \int_{0}^{\ln 4} e^{xy} \phantom{x}dy}\right ]\phantom{x}dx\\&= \int_{0}^{1} x \left[\left(\dfrac{1}{x}e^{xy} \right ) \right ]_{0}^{\ln 4} \phantom{x}dx\\&= \int_{0}^{1} (e^{x \cdot \ln 4} – e^{x \cdot 0}) \phantom{x}dx\\&= \int_{0}^{1} (4^x – 1) \phantom{x}dx\end{aligned}

Now, integrate the resulting expression with respect to $x$. Use the fact that $\int a^x \phantom{x}dx = \dfrac{a^x}{\ln a} + C$.

\begin{aligned}\int_{0}^{1} (4^x – 1) \phantom{x}dx &=\int_{0}^{1} 4^x  \phantom{x}dx – \int_{0}^{1} 1 \phantom{x}dx\\&= \left[\dfrac{4^x}{\ln 4} \right ]_{0}^{1} – [x]_{0}^{1}\\&= \left(\dfrac{4}{\ln 4} – \dfrac{1}{\ln 4} \right ) – (1 – 0)\\&= \dfrac{3}{\ln 4} – 1\\&\approx 1.16 \end{aligned}

Hence, the iterated integral is equal to $\dfrac{3}{\ln 4} – 1$ or approximately equal to $1.16$.

Practice Questions

1. Calculate the double integral, $\int \int_R (4x + 6y^2) \phantom{x}dA$, over the rectangular region, $R = [0, 2] \times [1, 4]$.
2. Calculate the double integral, $\int \int_R \dfrac{1}{(x + 2y)^2} \phantom{x}dA$, over the rectangular region, $R = [0, 1] \times [0, 2]$.
3. Calculate the iterated integral, $\int \int_R 2xy^2 \phantom{x}dA$, over the rectangular region, $R = [y, y^3] \times [0, 2]$.
4. Calculate the iterated integral, $\int \int_R \sin y \phantom{x}dA$, over the rectangular region, $R = [0, y] \times [0, \pi]$.
5. Calculate the iterated integral, $\int \int_R 2xe^{3xy} \phantom{x}dA$, over the rectangular region, $R = [0, 2] \times [0, \ln 2]$.
6. Calculate the iterated integral, $\int \int_R x^3 e^{y^3} \phantom{x}dA$, over the rectangular region, $R = [x^2, 9] \times [0, 3]$.

Answer Key

1. $\int_{0}^{2} \int_{1}^{4} (4x + 6y^2) \phantom{x}dxdy = 108$
2. $\int_{1}^{2} \int_{1}^{2} \dfrac{1}{(x + 2y)^2} \phantom{x}dxdy = \ln \left(2\right) + \dfrac{-\ln \left(6\right) + \ln \left(5\right) – \ln \left(3\right)}{2} \approx 0.053$
3. $\int_{0}^{4} \int_{y}^{y^3} 2xy^2 \phantom{x}dxdy = \dfrac{2272}{45} \approx 50.489$
4. $\int_{0}^{\pi} \int_{0}^{y} \sin y\phantom{x}dxdy = \pi \approx 3.14$
5. $\int_{0}^{2} \int_{0}^{\ln 2} 2xe^{3xy}\phantom{x}dydx = \dfrac{14}{\ln 2} -\dfrac{4}{3} \approx 18.86$
6. $\int_{x^2}^{9} \int_{0}^{3} x^3 e^{y^3} \phantom{x}dydx = \dfrac{1}{12} (e^{729} – 1) $

Images/mathematical drawings are created with GeoGebra.