JUMP TO TOPIC
The Sine Rule – Explanation & Examples
When you have understood the angles and sides of the triangles and their properties, you can move on to the next essential rule. We saw that a missing angle of a triangle could be easily calculated when given two other angles because we know that the sum of all angles of a triangle equal to 180 degrees.
But how will you find a missing angle when you are given only one angle and two sides, or how will you find a missing side when you are given two angles and one side?
That’s where the confusion begins!
But don’t worry, 11th-century mathematician Ibn Muaadh al-Jayyani found the solution in his book “The book of unknown arcs of a sphere.”
He presented a general Law of Sines, which was taken further by Nasir al-Din in the 13th century. He presented the Law of Sines for a plane and spherical triangles, which are very important in the calculations of parameters of triangles. Along with that, he also gave proof of this law.
In this article, you will learn about:
- The law of sines,
- the law of sine formula, and
- how to do the law of sines.
What is the Law of Sines?
The law of sines or sometimes referred to as the sine rule, is a rule that relates the sides of a triangle with the sine of their opposite angles.
Before proceeding to the law of sines, let’s first understand the meaning of the term sine.
Consider a right triangle ABC below.
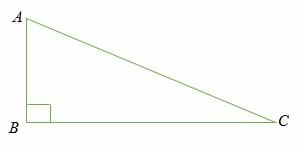
Given that AC is the hypotenuse of the right triangle ABC, then the sine of angle BCA is equal to the ratio of length AB to the length AC.
Sine < BCA = AB/AC
Similarly, the sine of angle BAC is equal to the ratio of length BC to the length AC.
Sine <BAC = BC/AC
Therefore, the sine of an angle is the ratio of the opposite side length of angle to the length of the hypotenuse.
Now, consider an oblique triangle ABC shown below. An oblique triangle is without a right angle (a triangle without a 90 – degree angle). This triangle’s three angles are denoted with capital letters, while the opposite sides are denoted with lower case letters. Note that each side and its opposite angle have the same letter.
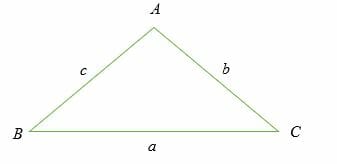
According to the law of sines.
a/Sin (A) = b/Sin (B) = c/Sin (C)
One real-life application of the sine rule is the sine bar, which is used to measure the angle of tilt in engineering.
Other common examples include measuring distances in navigation and the measurement of the distance between two stars in astronomy.
The Sine Rule Formula?
The law sine rule formula is given by
a/Sine (A) = b/Sine (B) = c/Sine (C) or Sine (A)/a = Sine (B)/b = Sine (C)/c
where a, b, and c are the side lengths opposite to angles A, B and C respectively.
How to Do the Law of Sines?
We can use the law of sine to calculate both the sides of a triangle and the angles of a triangle.
If you want to calculate the length of a side, you need to use the version of the sine rule where the lengths are the numerators:
a/Sine (A) = b/Sine (B) = c/Sine (C)
You will only ever need two parts of the sine rule formula, not all three. You will need to know at least one pair of a side with its opposite angle.
If you want to calculate an angle’s size, you need to use the sine rule version, where the angles are the numerators.
Sine (A)/a = Sine (B)/b = Sine (C)/c
As before, you will only need two parts of the sine rule, and you still need at least a side and its opposite angle.
Let’s work out a couple of example problems based on the sine rule.
Example 1
Given that sine (A) = 2/3, calculate angle ∠ B as shown in the triangle below.
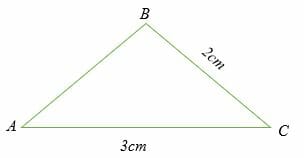
Solution
Since we are asked to calculate the size of an angle, then we will use the sine rule in the form:
Sine (A)/a = Sine (B)/b
By substitution,
(2/3)/2 = sine (B)/3
3(2/3) = 2 sine B
2 = 2 sine B
Divide both sides by 2
1 = sine B
Find the sine inverse of 1 using a scientific calculator.
Sine-1 1 = B
Therefore, ∠B = 90˚
Example 2
Calculate the length of side BC of the triangle shown below.
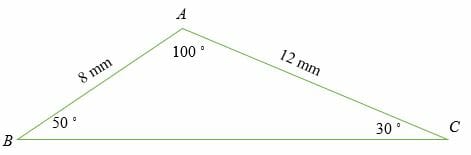
Solution
Because we need to calculate the length of the side, we, therefore, use the sine rule in the form of:
a/sine (A) = b/sine (B)
Now substitute.
a/sine 100 ˚ = 12/sine 50 ˚
Cross multiply.
12 sine 100 ˚= a sine 50 ˚
Divide both sides by sine 50 ˚
a = (12 sine 100 ˚)/sine 50 ˚
By using a calculator, we get;
a = 15.427
Thus, the length of side BC is 15.427 mm.
Example 3
Calculate the missing lengths of the following triangle.
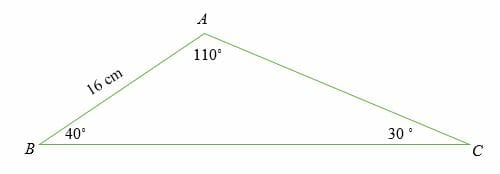
Solution
a/sine (A) = b/sine (B) = c/ sine (C)
By substitution, we have,
a/sine 110 ˚ = 16/sine 30 ˚
Cross multiply
a = (16 sine 110 ˚)/sine 30 ˚
a = 30.1
Solve for b.
b/sine 40 ˚ = 16/sine 30 ˚
b = (16 sine 40 ˚)/sine 30 ˚
= 20.6
Therefore, length BC = 30. 1 cm and length AC = 20.6 cm.
Example 4
Calculate the angles of the triangle shown below.
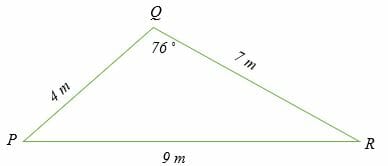
Solution
Apply the sine rule in the form;
sine(Q)/q = Sine (P)/p = Sine R/r
(Sine 76 ˚)/9 = sine (P)/7
Solve for angle P
Cross multiply.
7 Sine 76 ˚ = 9 sine P
Divide both sides by 9
Sine P = 7/9 sine 76 ˚
Sine P = 0.7547
Find the sine inverse of 0.7547.
Sine -1 0.7547 = P
P = 48.99 ˚
Solve for angle R
Sine R/4 = Sine 76 ˚/9
Cross multiply.
9 Sine R = 4 sine 76 ˚
Divide both sides by 9
Sine R = 4/9 sine 76 ˚
Sine R = 0.43124.
Sine -1 0.43124 = R
R = 25.54 ˚
