Less than – Explanation & Examples

What is the Less than Sign?

In Mathematics, the less-than sign is an important symbol used to describe inequality between two variables. The symbol used to denote the less than expression is “<.”

This symbol resembles two equal measure strokes that join in the acute angle at the right. It was found in the 1560s and typically placed in between the two values, which are getting compared, and indicates that the first number is less than the second number.

The typical usage of the less than symbol compares two quantities where the first variable is the smaller unit and the second variable is the larger unit. The less than symbol is usually an approximation of the opening angle bracket.

Example 1

a. 5 < 9: This implies that, 5 is less than 9

b. 0.7 < 1.5: Implies that 0.7 is less than 1.5

c. -0.6 < -0. 1: Implies that, -0.6 is less than -0.1

How to Remember the Less than Sign?

The easiest way to remember the less than symbol is to use the alligator method. As it is known that the alligator’s mouth always points to the largest value, the reason being it can swallow as much food as possible.

The alligator’s mouth normally opens to the right to denote the less than inequality.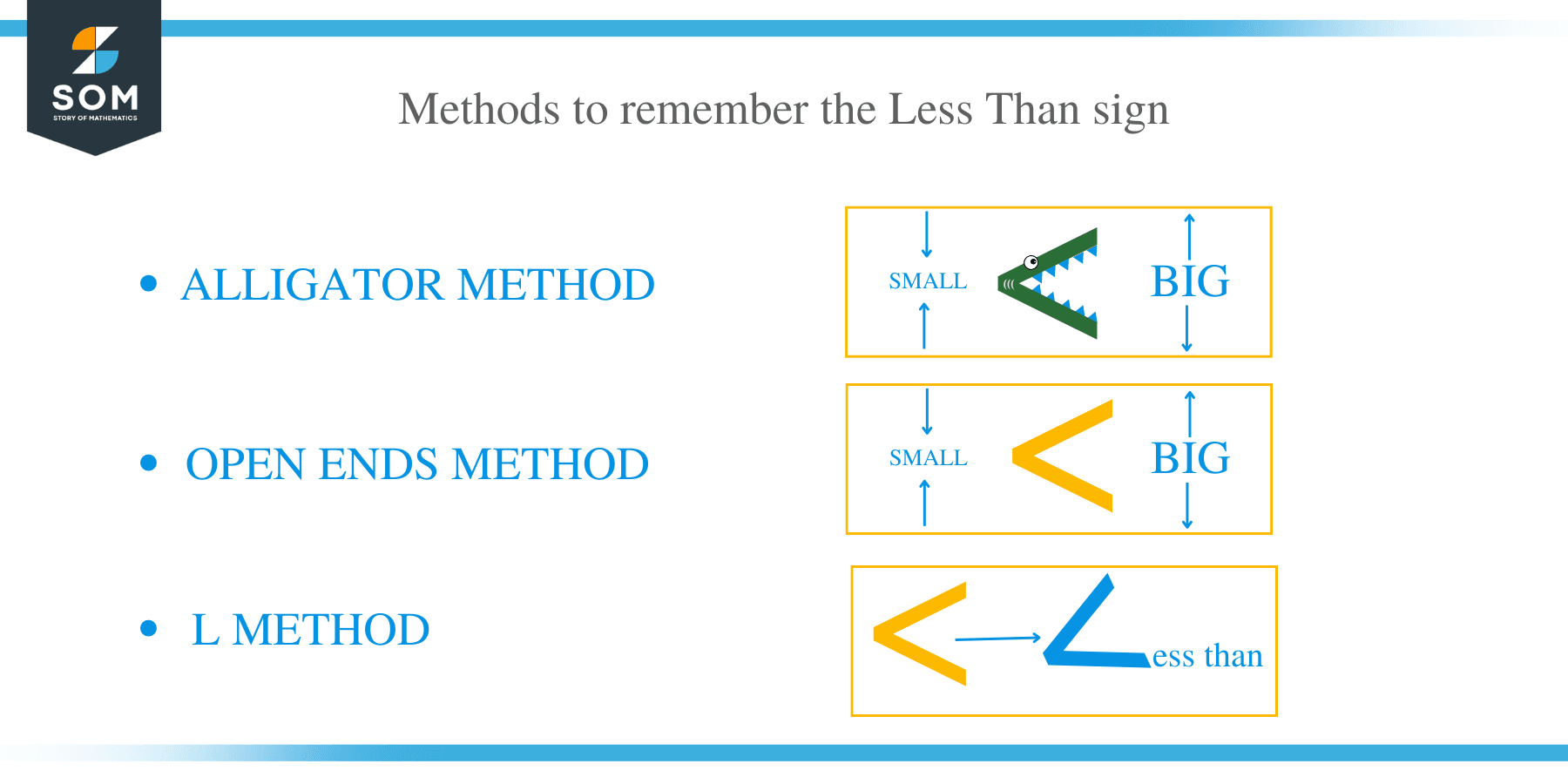

How to Use it?

To solve problems involving less than symbol, consider the following strategies and steps:

• Go through the complete problem to understand the situation.
• Highlight important keywords to help in solving the problem
• Identify the variables
• Write down the equations
• Solve the inequalities

Let’s understand this concept with the help of examples.

Example 2

Janet’s end-year profit of $150 is at least $11 less than the previous year. Determine her profit as an inequality.

Solution

Given that her profit of $150 is at least $11 less than the previous year.

Let p be the profit decrease between the two years;

There, we can represent this situation in an inequality expression as:

-11+P ≤ 150

Her profit this year is thus;

P ≤ $161

Example 3

Allan is under 18 years. How old is he?

Solution

Since we don’t know the exact age of Allan, then we can represent this situation as:

Let the age of Allan be x years;

So, write his age as:

x < 18

Note that the arrow points to the age “x” because the age is smaller than 18

Example 4

Solve the inequality:

2x + 5 < 7

The basic strategy for solving inequality problems is assuming the less than sign as the equal sign. Isolate x on one side and move +5 to the right side.

2x < 7 -5

= 2x < 2

Simplify by dividing 2 on both sides.

x < 1

Example 5

Workout the inequality: 3y < 15

Solution

Simplify by dividing 3 on both sides;

3y/3 < 15/3

y < 5

Example 6

Solve: 12 < x + 5

Solution

Subtract 5 from both sides;

12 − 5 < x + 5 − 5

7 < x Alternatively, the answer can be written as: x > 7

Example 7

Workout: x−3/2 < −5

Solution

First, eliminate the denominator of the fraction by multiply each variable with 2;

2x−3/2 ×2 < −5 ×2

2x−3 < −10

2x < −10 + 3

x < −7/2

Example 8

Pedro and Rooney play on the same football team. In the last game Pedro scored 3 more goals than Rooney. If the total goals scored by the two players were 9 goals. Calculate the possible number of goals scored by Rooney.

Solution

Assign Letters:

Let the goals scored by Pedro = p

And the goals scored by Rooney = r

Since Pedro scored more goals tha Rooney, therefore: p = r + 3

We know that the total scores were less than 9: p + r < 9

To find the possible number of goals scored by Rooney, solve:

p + r < 9

p = r + 3, therefore, p + (p + 3) < 9

Solve for the value of p;

2p + 3 < 9

Subtract 3 from both sides

2p < 9 − 3

Simplify:

2p < 6

P < 3

Therefore, the possible goals scored by Rooney can be 0, 1, and 2. The statement says that, Pedro scored 3 more goals than Rooney. And so, Pedro could have scored 3, 4, or 5 goals.