Introduction to Logarithms – Explanation & Examples

Before getting into the topic of logarithms, it is important we briefly discuss exponents and powers.

The exponent of a number is the frequency or number of times a number is multiplied by itself. An expression that represents repeated multiplication of the same factor is called a power.

For example, the number 16 can be expressed in exponential form as; 2⁴. In this case, the numbers 2 and 4 are the base and exponent, respectively.

What is a Logarithm?

On the other hand, the logarithm of a number is the power or index to which a given base must be raised to obtain the number.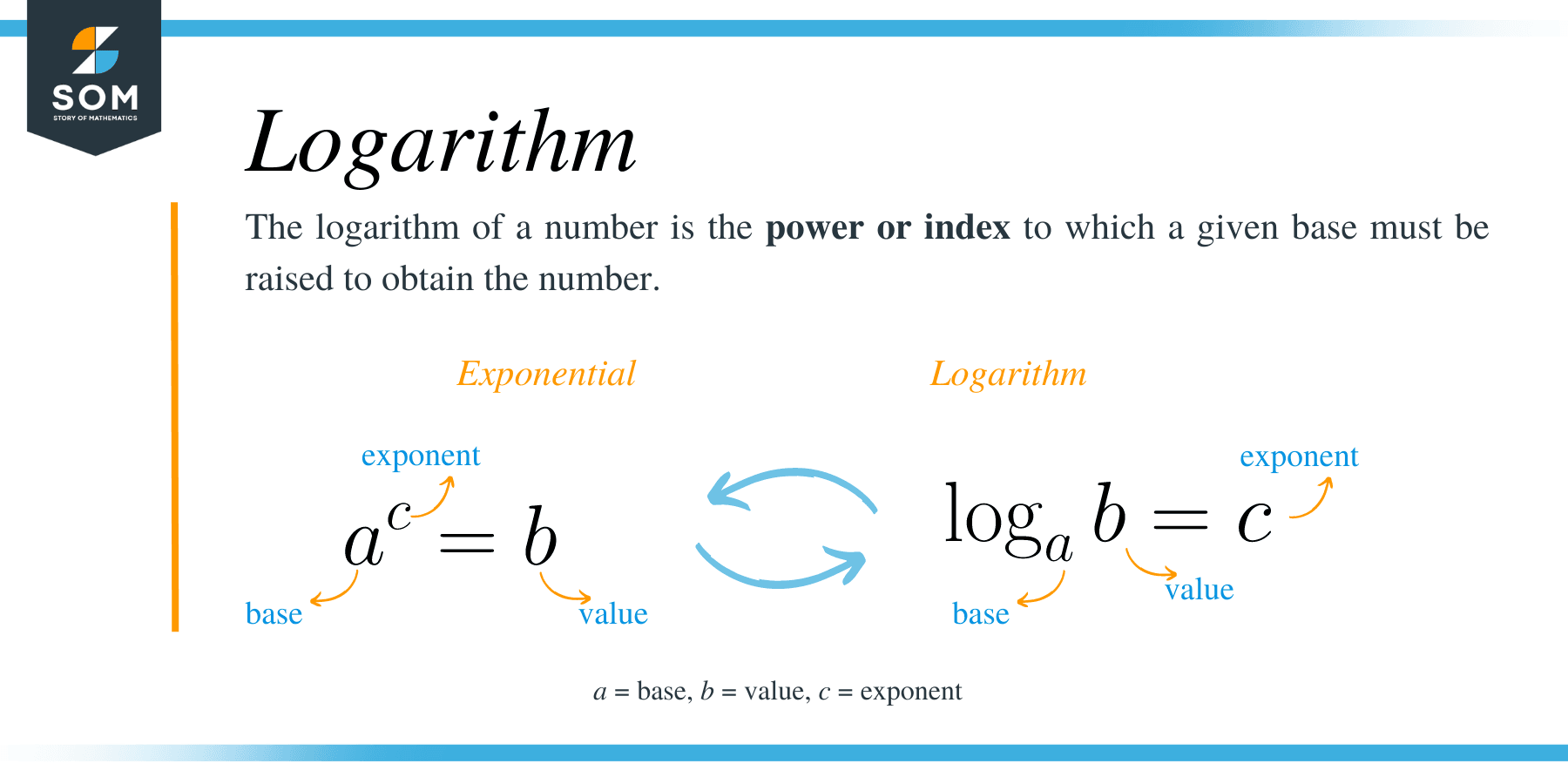

The concept of logarithm was introduced in the 17^th century by a Scottish mathematician named John Napier.

It was introduced to mechanical machinery in the 19^th century and to computers in the 20^th century. The natural logarithm is one of the useful functions in mathematics and has many applications.

Consider three numbers a, x and n, which are related as follows;

a^x = M; where a > 0 < M and a ≠ 1

The number x is the logarithm of the number n to the base ‘a’. Therefore, a^x = n can be expressed in logarithmic form as.

log _a M = x, Here, M is the argument or the number; x is the exponent while ‘a’ is the base.

For example:

16 = 2 ⁴ ⟹ log ₂ 16 = 4

9 = 3² ⟹ log ₃ 9 = 2
625 = 5⁴ ⟹ log ₅ 625 = 4
7⁰ = 1 ⟹ log ₇ 1 = 0
3^{– 4} = 1/3⁴ = 1/81 ⟹ log ₃ 1/81 = -4

The common logarithms

All the logarithms with base 10 are called common logarithms. Mathematically, the common log of a number x is written as:

log ₁₀ x = log x

The natural logarithms

A natural logarithm is a special form of logarithms in which the base is mathematical constant e, where e is an irrational number and equal to 2.7182818…. Mathematically, the natural log of a number x is written as:

log _e x = ln x

where the natural log or ln is the inverse of e.

The natural exponential function is given as:

e ^x

The negative logarithms

We know that logarithms are not defined for negative values.

Then what do we mean by the negative logarithms?

It means that the logarithm of the set of such numbers gives a negative result. All the numbers that lie between 0 and 1 have negative logarithms.

Basic Laws of Logarithms

There are four basic rules of logarithms. These are:

• Product rule.

The product of two logarithms with a common base is equal to the sum of individual logarithms.

⟹ log _b (m n) = log _b m + log _b n.

• Division rule

The division rule of logarithms states that the quotient of two logarithmic values with the same bases is equal to each logarithm’s difference.

⟹ log _b (m/n) = log _b m – log _b n

• The exponential rule of logarithms

This rule states that the logarithm of a number with a rational exponent is equal to the product of the exponent and its logarithm.

⟹ log _b (m ⁿ) = n log _b ^m

• Change of Base

⟹ log _b a = log _x a ⋅ log _b x

⟹ log _b a = log _x a / log _x b

NOTE: The logarithm of a number is always stated together with its base. If the base is not given, it is assumed to be 10.

For example, log 100 = 2.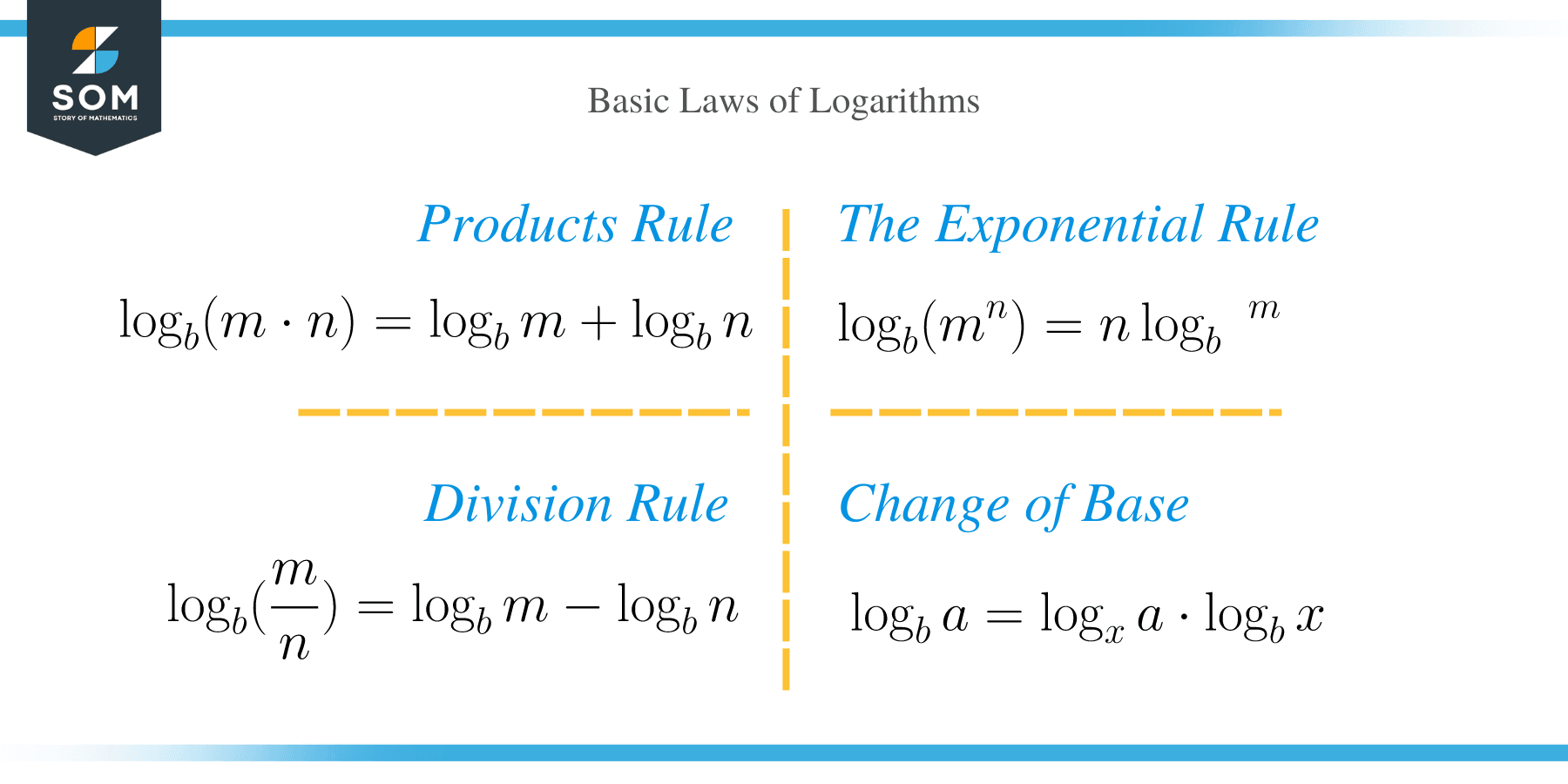

Real-life application of logarithms

Logarithms very useful in the field of science, technology, and mathematics.

Here are a few examples of real-life applications of logarithms.

• Electronic calculators have logarithms to make our calculations much easier.
• Logarithms are used in surveys and celestial navigation.
• Logarithms can be used to calculate the level of noise in decibels.
• Ratio active decay, acidity [PH] of a substance and Richter scale are all measured in logarithmic form.

Let’s solve a few problems involving logarithms.

Example 1

Solve for x in log ₂ (64) = x

Solution

Here, 2 is the base, x is the exponent and 64 is the number.

Let 2^x = 64

Express 64 to the base of 2.

2^x = 2 × 2 × 2 × 2 × 2 × 2 = 2⁶

x = 6, therefore, log ₂ 64 = 6.

Example 2

Find x in log₁₀ 100 = x

Solution

100 = number

10 = base

x = exponent

Therefore, 10 ^x = 100

Hence x = 2

But 100 = 10 * 10 = 10²

Example 3

Solve for k given, log₃ x = log₃ 4 + log₃ 7

Solution

By applying the product rule log _b (m n) = log _b m + log _b n we get;

⟹ log₃ 4 + log₃ 7= log ₃ (4 * 7) = log ₃ (28).

Hence, x = 28.

Example 4

Solve for y given, log ₂ x = 5

Solution

Here, 2 = base

x = number

5 = exponent

⟹ 2⁵ = x

⟹ 2* 2 * 2 * 2 * 2 = 32

Thus, x = 32

Example 5

Solve for log ₁₀ 105 given that, log ₁₀ 2 = 0.30103, log ₁₀ 3 = 0.47712 and log ₁₀ 7 = 0.84510

Solution

log₁₀ 105 = log₁₀ (7 x 5 x 3)

Apply the product rule of logarithms
= log₁₀ 7 + log₁₀ 5 + log₁₀ 3
= log₁₀ 7 + log₁₀ 10/2 + log₁₀ 3
= log₁₀ 7 + log₁₀ 10 – log₁₀ 2 + log₁₀ 3
= 0.845l0 + 1 – 0.30103 + 0.47712
= 2.02119.