- Home
- >
- Multiplication – Explanation & Examples
JUMP TO TOPIC
Multiplication – Explanation & Examples
 What is Multiplication?
What is Multiplication?
Multiplication is a mathematical operation of finding the result of two or more numbers by repeated numbers’ additions.
Multiplication is usually denoted by a cross sign (x). However, other symbols such as an asterisk (*), dot(.), and the phrase “times” are also used.
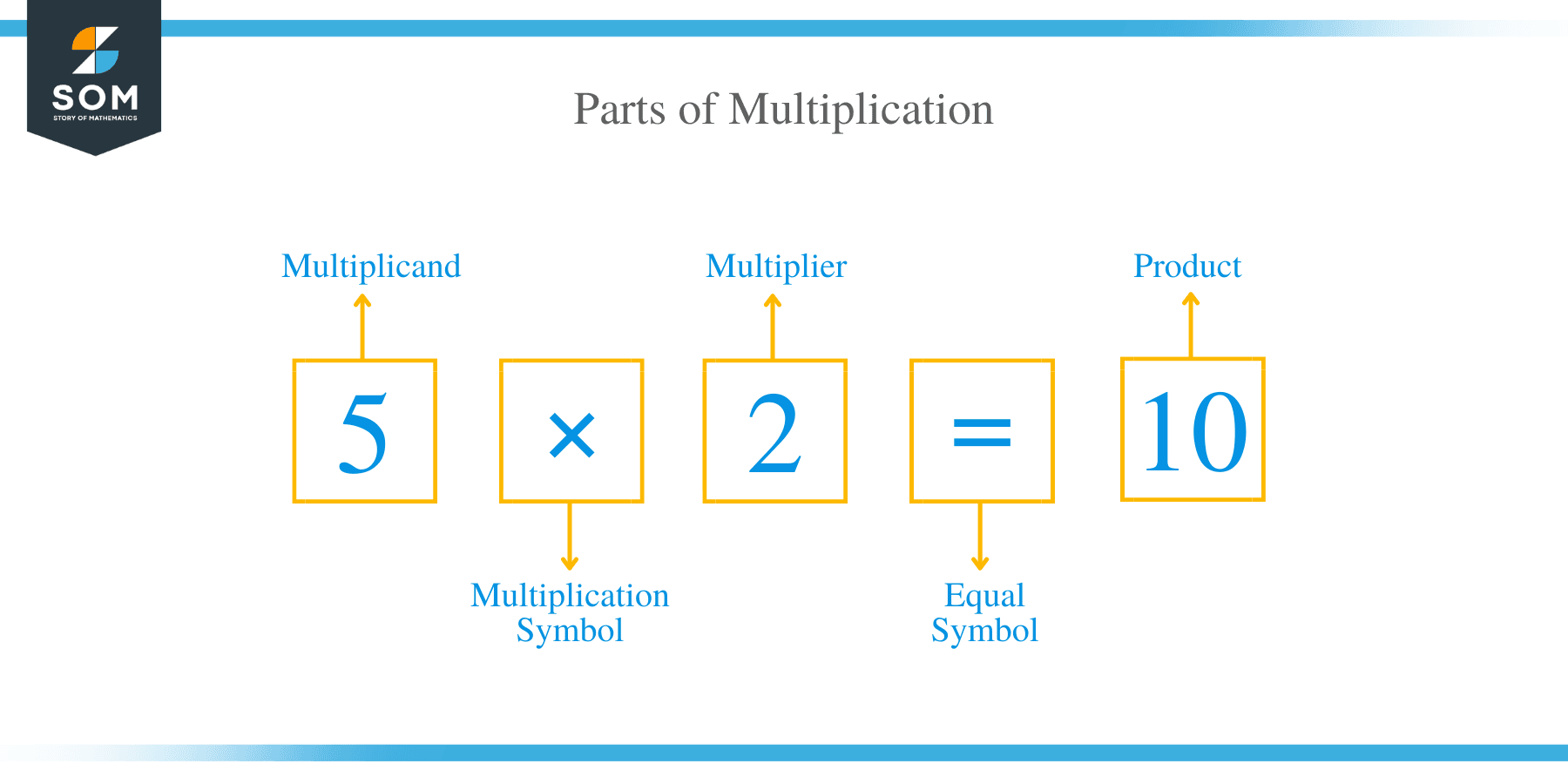
Parts of Multiplication
A multiplication sentence consists of two parts, namely the mathematical expression and the product. A mathematical expression consists of factors and the operator or symbol of multiplication.
For example, in a mathematical expression: 5 x 2 = 10, the portion “2 x 5” is the mathematical expression composed of 2 and 5 as factors and operators. The product, in this case, is 10.
We can further breakdown factors into multiplicand and multiplier:
- A multiplicand is a number multiplied by another number.
- A multiplier is a number with which to multiply.
- Product is a result of multiplying.

Properties of Multiplication
Learning properties of multiplication helps simplify and solve mathematical problems involving multiplication.
- Commutative
In multiplication, the commutative property implies that the multiplication of two or more numbers does not affect the final answer. In general, for a multiplication sentence: m x n = n x m. For example, 4 x 5 is the same as 5 x 4. This property also applies when multiplying a large group of numbers. For instance, 4 x 3 x 2 = 2 x 3 x 4.
- Associative
In multiplication, the associative property states that grouping of the numbers does not affect the ultimate answer when multiplying a series of numbers together. Generally, groupings in any mathematical expression are indicated by parentheses or brackets. We can summary this property as: m x (n x p) = (m x n) x p. For example, (2 x 4) x 6 = 2 x (4 x 6).
- Identity
This property states that the multiplication of any number with number one does not change its value. In other words, this property can be written as 1 x a = a. For example, 1 x 8 = 8.
- Distributive
The distributive property for multiplication states that an expression consisting of the addition or subtraction of values multiplied by a number is equivalent to the sum or difference of the expression numbers.
In general, m x (n + p) = m x n + m x p, and m x (n – p) = m x n – m x p. For example, 2 x (3 + 4) = 2 x 3 + 2 x 4.
Multiplication Chart
An array is a grid/multiplication chart consisting of numbers in rows and columns. Multiplication using a multiplication chart is easier because the product between two numbers is found by counting the number of rows and multiplying by the corresponding number of columns.
For example, in a grip consisting of 9 in the column and 6 in the row, the product in the grid is 54.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
How to Create Multiplication Sentences?
Learning how to create multiplication sentences is an essential skill to learners as it prepares them how to use mathematics practically. A student who knows how to create his/her own multiplication sentences can look at a four-by-four grid of numbers and will definitely tell that the grid consists of 16 items.
How to Create a Sentence from a Word Problem
Creating multiplication sentences seems to throw students off. However, by reading and understanding this article, solving word problems should be easier for the students.
For instance, suppose Mary collected a basket of oranges if she has enough oranges to place 15 oranges per 3 rows. How many oranges did she collect? In this example, the multiplication sentence can be written as 15 x 3 = 45. Therefore, Mary collected 45 oranges.