- Home
- >
- Multiplying and Dividing Integers – Methods & Examples
Multiplying and Dividing Integers – Methods & Examples
 In mathematics, arithmetic operation with integers involves subtracting, adding, dividing and multiplying all types of real numbers. In particular, integers are numbers that include positive, negative and zero numbers. Multiplication and division of integers are governed by similar rules.
In mathematics, arithmetic operation with integers involves subtracting, adding, dividing and multiplying all types of real numbers. In particular, integers are numbers that include positive, negative and zero numbers. Multiplication and division of integers are governed by similar rules.
How to Multiply Integers?
Multiplication is defined as repeated addition of integers. Multiplication of integers includes three cases:
- Multiplication of two positive integers
- Multiplication between two negative integers
- Multiplication between a positive and a negative integer.
Multiplication of two integers with like sign will always give out a positive product. This means that the product of two positive or two negative integers is positive. On the other hand, the product integers with unlike sign will always be negative.
Many students are faced with a challenge of remembering the above rules of multiplying integers. This article has a come up with some scenario to help you avoid the confusion. In this, scenario, the positive sign (+) has been used to denote ‘GOOD’ while a negative sign symbolizes the phrase ‘BAD. ‘Let’s take a look at these mnemonics.
- If good (+) things happens to good (+) people, then it is good (+)
- If good (+) things happens to bad (-) people, then it is bad (-)
- If bad (-) things happen to good (+) people, then it is bad (-)
- If bad (-) things happen to bad (-) people, then it is good (+)
To multiply integers, just multiply the numeric numbers without the sign and place a sign on the product by recalling the above rules.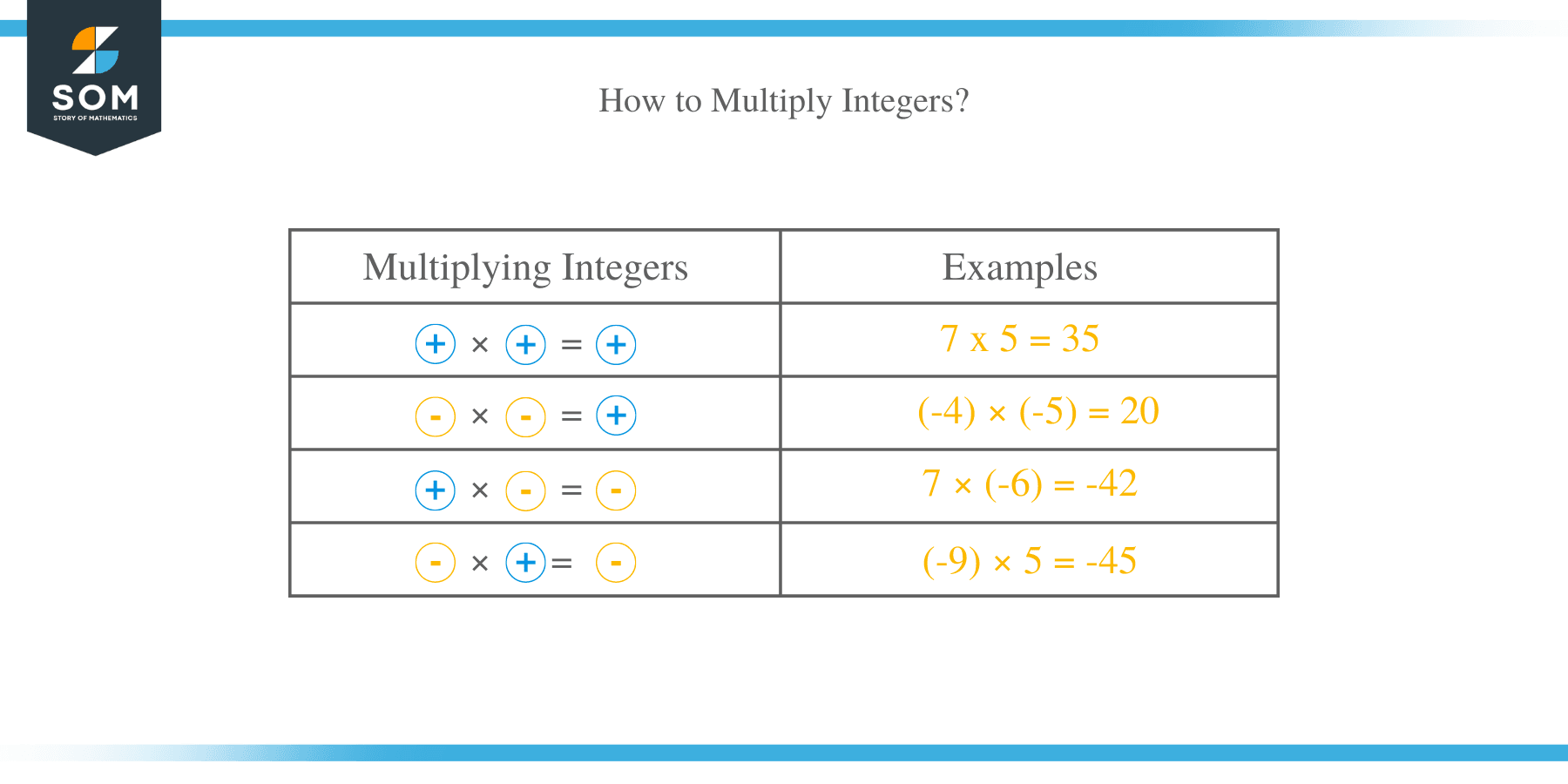
Example 1
- 7 x 5 = 35
- 7 × (-6) = -42
- (-9) × 5 = -45
- (-4) × (-5) = 20
If the number of negative multiplicands in a multiplication sentence is odd, the product will be a negative number.
Example 2
(-2) × (−4) × (−3) = −24; here, the number of multiplicands = 3 (odd number)
When the number of negative multiplicands is even in a multiplication sentence, the product will be positive.
Example 3
(−4) × (−3) = 12; Here the number of multiplicands is 2 (even)
How to Divide Integers?
While multiplication is totaling of integers, division on the other hand is the distribution of integers. We can simply say that, division is the inverse of multiplication. The rules of dividing integers are similar to the rules of multiplication. The only difference in division is that the quotient may not necessary be an integer.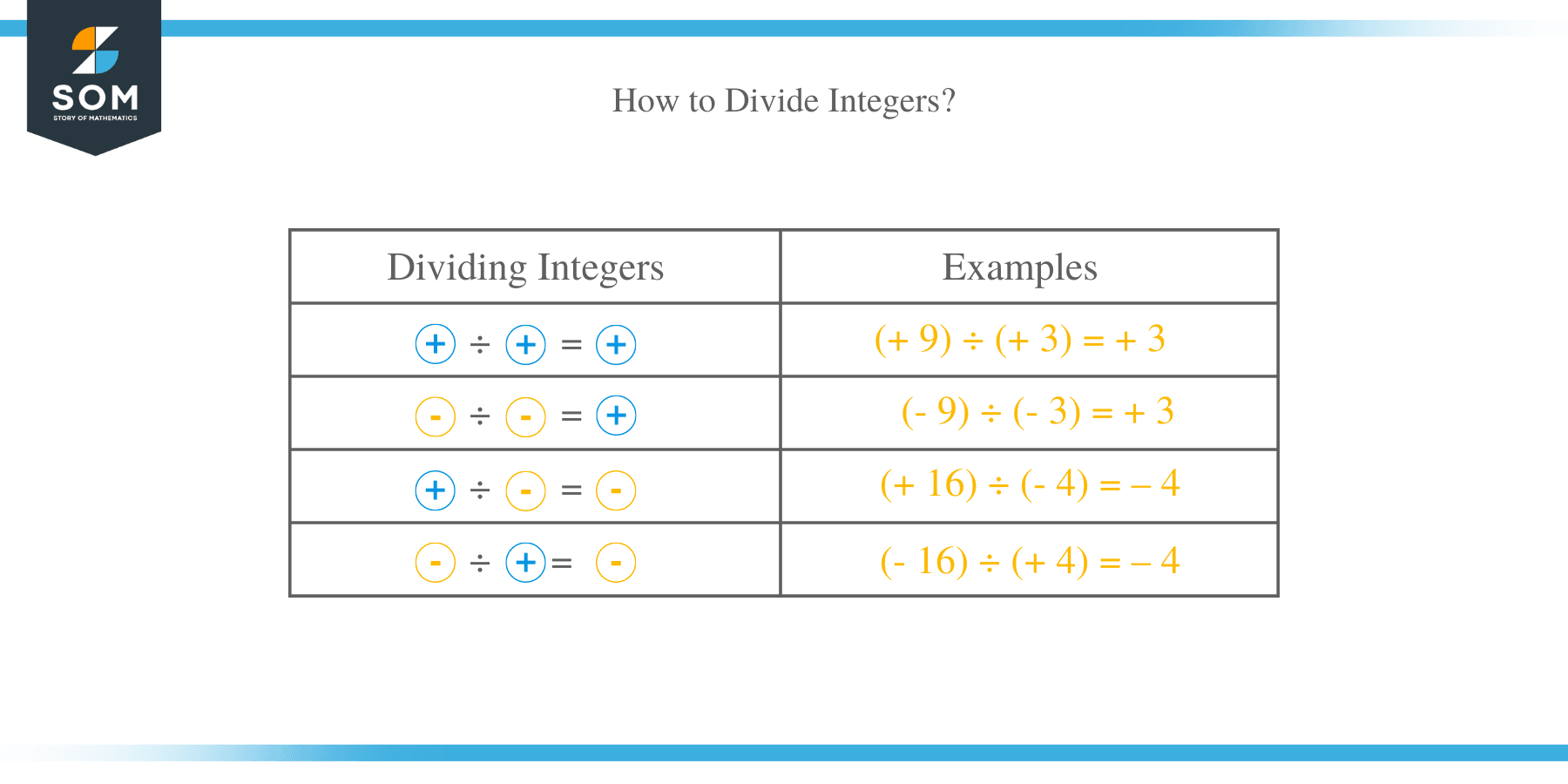
Let’s also take a look at the rules of division:
- The quotient of positive integer is always positive. If both the dividend and divisor are positive integers, the value of the quotient will be positive. For example, (+ 9) ÷ (+ 3) = + 3
- The quotient of two negative numbers is always positive. This means that, if the dividend and the divisor are both negative, then the quotient is always positive. For example;
(- 9) ÷ (- 3) = + 3
Hence, when dividing two integers with like signs, we divide the numbers without sign and place a positive sign to the result. - The division of a positive and a negative integer results in a negative answer. For example; (+ 16) ÷ (- 4) = – 4
Thus, to divide integers with unlike signs, we divide the numerical values without signs and place a minus sign to the result.
