Home
>
Normal Probability Plot – Explanation & Examples

JUMP TO TOPIC

1. What is a normal probability plot?
2. How to make a normal probability plot?
- – Example 1
- – Example 2
3. How to read a normal probability plot?
4. Practice questions
5. Answer key

Normal Probability Plot – Explanation & Examples

The definition of the normal probability plot is:

“The normal probability plot is a plot used to assess the normal distribution of numerical data.”

In this topic, we will discuss the normal probability plot from the following aspects:

What is a normal probability plot?
How to make a normal probability plot?
How to read a normal probability plot?
Practice questions.
Answer key.

1. What is a normal probability plot?

The normal probability plot is a plot used to assess the normal distribution of any numerical data.

Making a histogram of your data can help you decide whether or not a set of data is normal, but there is a more specialized type of plot you can create, called a normal probability plot.

If the data follow a normal distribution then a normal probability plot of the theoretical percentiles of the normal distribution on the x-axis versus the observed sample percentiles on the y-axis should be approximately linear.

The theoretical p% percentile of a normal distribution is the value such that p% of the values are lower than that value.

The sample p% percentile of any numerical data is the value such that p% of the measurements fall below that value.

For example, the 50% percentile or the median is the value so that 50% or half of your measurements fall below that value.

Another example, the 27% percentile is the value so that 27% of the data points in your numerical data fall below that value.

2. How to make a normal probability plot?

We will go through several examples.

– Example 1

The following are the weights (in kg) of 100 persons from a certain survey.

52.44 52.77 54.56 53.07 53.13 54.72 53.46 51.73 52.31 52.55 54.22 53.36 53.40 53.11 52.44 54.79 53.50 51.03 53.70 52.53 51.93 52.78 51.97 52.27 52.37 51.31 53.84 53.15 51.86 54.25 53.43 52.70 53.90 53.88 53.82 53.69 53.55 52.94 52.69 52.62 52.31 52.79 51.73 55.17 54.21 51.88 52.60 52.53 53.78 52.92 53.25 52.97 52.96 54.37 52.77 54.52 51.45 53.58 53.12 53.22 53.38 52.50 52.67 51.98 51.93 53.30 53.45 53.05 53.92 55.05 52.51 50.69 54.01 52.29 52.31 54.03 52.72 51.78 53.18 52.86 53.01 53.39 52.63 53.64 52.78 53.33 54.10 53.44 52.67 54.15 53.99 53.55 53.24 52.37 54.36 52.40 55.19 54.53 52.76 51.97.

Draw a normal probability plot of this data.

1. Order the numbers from smallest to largest number.

50.69 51.03 51.31 51.45 51.73 51.73 51.78 51.86 51.88 51.93 51.93 51.97 51.97 51.98 52.27 52.29 52.31 52.31 52.31 52.37 52.37 52.40 52.44 52.44 52.50 52.51 52.53 52.53 52.55 52.60 52.62 52.63 52.67 52.67 52.69 52.70 52.72 52.76 52.77 52.77 52.78 52.78 52.79 52.86 52.92 52.94 52.96 52.97 53.01 53.05 53.07 53.11 53.12 53.13 53.15 53.18 53.22 53.24 53.25 53.30 53.33 53.36 53.38 53.39 53.40 53.43 53.44 53.45 53.46 53.50 53.55 53.55 53.58 53.64 53.69 53.70 53.78 53.82 53.84 53.88 53.90 53.92 53.99 54.01 54.03 54.10 54.15 54.21 54.22 54.25 54.36 54.37 54.52 54.53 54.56 54.72 54.79 55.05 55.17 55.19.

2. Assign a rank to each value of your data.

weight	rank
50.69	1
51.03	2
51.31	3
51.45	4
51.73	5
51.73	6
51.78	7
51.86	8
51.88	9
51.93	10
51.93	11
51.97	12
51.97	13
51.98	14
52.27	15
52.29	16
52.31	17
52.31	18
52.31	19
52.37	20
52.37	21
52.40	22
52.44	23
52.44	24
52.50	25
52.51	26
52.53	27
52.53	28
52.55	29
52.60	30
52.62	31
52.63	32
52.67	33
52.67	34
52.69	35
52.70	36
52.72	37
52.76	38
52.77	39
52.77	40
52.78	41
52.78	42
52.79	43
52.86	44
52.92	45
52.94	46
52.96	47
52.97	48
53.01	49
53.05	50
53.07	51
53.11	52
53.12	53
53.13	54
53.15	55
53.18	56
53.22	57
53.24	58
53.25	59
53.30	60
53.33	61
53.36	62
53.38	63
53.39	64
53.40	65
53.43	66
53.44	67
53.45	68
53.46	69
53.50	70
53.55	71
53.55	72
53.58	73
53.64	74
53.69	75
53.70	76
53.78	77
53.82	78
53.84	79
53.88	80
53.90	81
53.92	82
53.99	83
54.01	84
54.03	85
54.10	86
54.15	87
54.21	88
54.22	89
54.25	90
54.36	91
54.37	92
54.52	93
54.53	94
54.56	95
54.72	96
54.79	97
55.05	98
55.17	99
55.19	100

Note that repeated values or ties are ranked sequentially as usual.

The first (smallest) value is 50.69 so its rank is 1, the next value is 51.03 so its rank is 2.

The last (largest) value is 55.19 so its rank is 100.

3. Calculate the cumulative probability (pi) associated with each rank (i) using the following formula:

pi=(i-a)/(n+1-2a)

Where:

i = 1,2,3,…..n. n is the number of data points.

a = 3/8 for n ≤ 10, and = 0.5 for n > 10.

Since the number of data points = 100 which is larger than 10, so the formula reduces to:

pi=(i-0.5)/n

The following table will be produced:

weight	rank	pi
50.69	1	0.005
51.03	2	0.015
51.31	3	0.025
51.45	4	0.035
51.73	5	0.045
51.73	6	0.055
51.78	7	0.065
51.86	8	0.075
51.88	9	0.085
51.93	10	0.095
51.93	11	0.105
51.97	12	0.115
51.97	13	0.125
51.98	14	0.135
52.27	15	0.145
52.29	16	0.155
52.31	17	0.165
52.31	18	0.175
52.31	19	0.185
52.37	20	0.195
52.37	21	0.205
52.40	22	0.215
52.44	23	0.225
52.44	24	0.235
52.50	25	0.245
52.51	26	0.255
52.53	27	0.265
52.53	28	0.275
52.55	29	0.285
52.60	30	0.295
52.62	31	0.305
52.63	32	0.315
52.67	33	0.325
52.67	34	0.335
52.69	35	0.345
52.70	36	0.355
52.72	37	0.365
52.76	38	0.375
52.77	39	0.385
52.77	40	0.395
52.78	41	0.405
52.78	42	0.415
52.79	43	0.425
52.86	44	0.435
52.92	45	0.445
52.94	46	0.455
52.96	47	0.465
52.97	48	0.475
53.01	49	0.485
53.05	50	0.495
53.07	51	0.505
53.11	52	0.515
53.12	53	0.525
53.13	54	0.535
53.15	55	0.545
53.18	56	0.555
53.22	57	0.565
53.24	58	0.575
53.25	59	0.585
53.30	60	0.595
53.33	61	0.605
53.36	62	0.615
53.38	63	0.625
53.39	64	0.635
53.40	65	0.645
53.43	66	0.655
53.44	67	0.665
53.45	68	0.675
53.46	69	0.685
53.50	70	0.695
53.55	71	0.705
53.55	72	0.715
53.58	73	0.725
53.64	74	0.735
53.69	75	0.745
53.70	76	0.755
53.78	77	0.765
53.82	78	0.775
53.84	79	0.785
53.88	80	0.795
53.90	81	0.805
53.92	82	0.815
53.99	83	0.825
54.01	84	0.835
54.03	85	0.845
54.10	86	0.855
54.15	87	0.865
54.21	88	0.875
54.22	89	0.885
54.25	90	0.895
54.36	91	0.905
54.37	92	0.915
54.52	93	0.925
54.53	94	0.935
54.56	95	0.945
54.72	96	0.955
54.79	97	0.965
55.05	98	0.975
55.17	99	0.985
55.19	100	0.995

4. Calculate the Z-score for each pi value (zi). The function qnorm of the R programming language finds the Z-score that is associated with each pi or probability.

For example, when pi = 0.5, the Z-score = 0.

qnorm(0.5)

## [1] 0

This is because the Z-score is for a normal distribution with mean = 0 and standard deviation = 1.

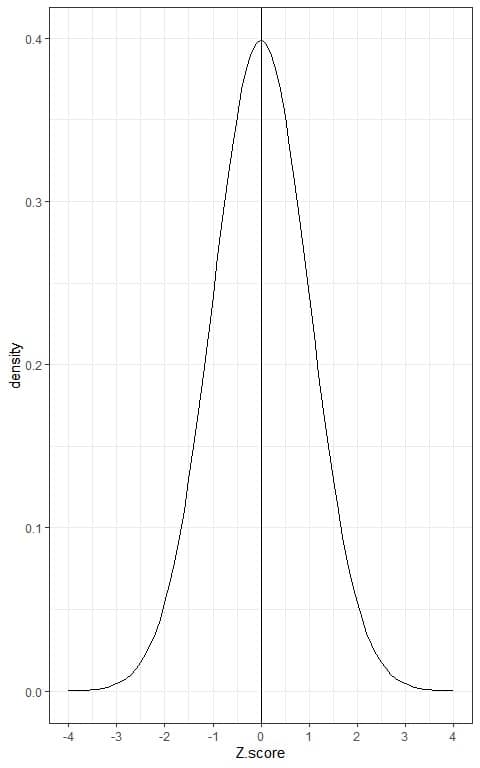
We know from the normal distribution properties that when the data value equals the mean or 0, the probability of data points < 0 = the probability of data points > 0 = 0.5.

As a result, the Z-score values are negative for every data point that has an associated p less than 0.5 and positive for those that have a p greater than 0.5.

The following table will be produced.

weight	rank	pi	zi
50.69	1	0.005	-2.58
51.03	2	0.015	-2.17
51.31	3	0.025	-1.96
51.45	4	0.035	-1.81
51.73	5	0.045	-1.70
51.73	6	0.055	-1.60
51.78	7	0.065	-1.51
51.86	8	0.075	-1.44
51.88	9	0.085	-1.37
51.93	10	0.095	-1.31
51.93	11	0.105	-1.25
51.97	12	0.115	-1.20
51.97	13	0.125	-1.15
51.98	14	0.135	-1.10
52.27	15	0.145	-1.06
52.29	16	0.155	-1.02
52.31	17	0.165	-0.97
52.31	18	0.175	-0.93
52.31	19	0.185	-0.90
52.37	20	0.195	-0.86
52.37	21	0.205	-0.82
52.40	22	0.215	-0.79
52.44	23	0.225	-0.76
52.44	24	0.235	-0.72
52.50	25	0.245	-0.69
52.51	26	0.255	-0.66
52.53	27	0.265	-0.63
52.53	28	0.275	-0.60
52.55	29	0.285	-0.57
52.60	30	0.295	-0.54
52.62	31	0.305	-0.51
52.63	32	0.315	-0.48
52.67	33	0.325	-0.45
52.67	34	0.335	-0.43
52.69	35	0.345	-0.40
52.70	36	0.355	-0.37
52.72	37	0.365	-0.35
52.76	38	0.375	-0.32
52.77	39	0.385	-0.29
52.77	40	0.395	-0.27
52.78	41	0.405	-0.24
52.78	42	0.415	-0.21
52.79	43	0.425	-0.19
52.86	44	0.435	-0.16
52.92	45	0.445	-0.14
52.94	46	0.455	-0.11
52.96	47	0.465	-0.09
52.97	48	0.475	-0.06
53.01	49	0.485	-0.04
53.05	50	0.495	-0.01
53.07	51	0.505	0.01
53.11	52	0.515	0.04
53.12	53	0.525	0.06
53.13	54	0.535	0.09
53.15	55	0.545	0.11
53.18	56	0.555	0.14
53.22	57	0.565	0.16
53.24	58	0.575	0.19
53.25	59	0.585	0.21
53.30	60	0.595	0.24
53.33	61	0.605	0.27
53.36	62	0.615	0.29
53.38	63	0.625	0.32
53.39	64	0.635	0.35
53.40	65	0.645	0.37
53.43	66	0.655	0.40
53.44	67	0.665	0.43
53.45	68	0.675	0.45
53.46	69	0.685	0.48
53.50	70	0.695	0.51
53.55	71	0.705	0.54
53.55	72	0.715	0.57
53.58	73	0.725	0.60
53.64	74	0.735	0.63
53.69	75	0.745	0.66
53.70	76	0.755	0.69
53.78	77	0.765	0.72
53.82	78	0.775	0.76
53.84	79	0.785	0.79
53.88	80	0.795	0.82
53.90	81	0.805	0.86
53.92	82	0.815	0.90
53.99	83	0.825	0.93
54.01	84	0.835	0.97
54.03	85	0.845	1.02
54.10	86	0.855	1.06
54.15	87	0.865	1.10
54.21	88	0.875	1.15
54.22	89	0.885	1.20
54.25	90	0.895	1.25
54.36	91	0.905	1.31
54.37	92	0.915	1.37
54.52	93	0.925	1.44
54.53	94	0.935	1.51
54.56	95	0.945	1.60
54.72	96	0.955	1.70
54.79	97	0.965	1.81
55.05	98	0.975	1.96
55.17	99	0.985	2.17
55.19	100	0.995	2.58

5. Create an x-y scatter plot of your z-score values on the x-axis versus their corresponding data points on the y-axis.

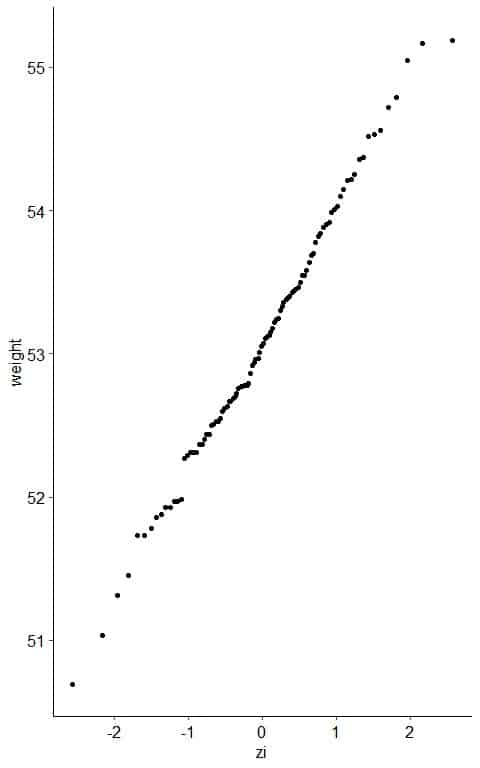
6. If the weight data are consistent with the normal percentiles from a normal distribution, the points should lie close to a straight line.

As a reference, a straight line can be added to the plot which passes through the first and third quartiles.

From the table, we see that the first quartile (at pi = 0.25) was about 52.50 kg and zi = -0.69 and third quartile (at pi = 0.75) was 53.69 kg and zi = 0.66.

The further the points vary from this line, the greater the indication of departure from normality.

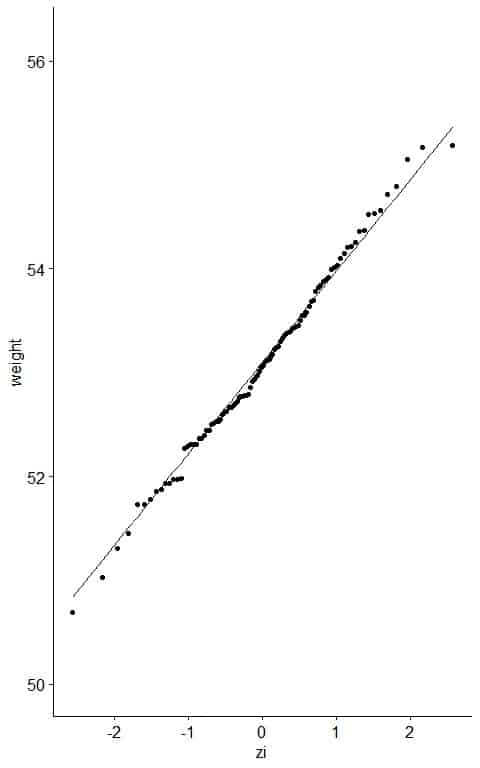
Nearly all the data are on the straight line, so it is normally distributed data.

– Example 2

The following is the ankle diameter in centimeters, measured as the sum of two ankles for 60 physically active individuals from a certain survey.

14.1 15.1 14.1 15.0 14.9 13.9 15.6 14.6 13.2 15.0 14.5 16.0 15.4 13.2 14.0 14.0 16.0 14.7 14.8 15.5 13.9 14.4 13.8 14.1 14.7 14.9 15.3 14.5 13.2 13.2 15.8 14.0 15.1 15.0 12.9 14.0 13.0 14.0 15.4 16.4 15.2 13.8 14.9 16.0 16.0 16.3 15.3 16.5 14.4 13.4 14.4 14.2 15.4 15.0 13.0 13.0 14.8 16.2 15.4 14.4.

Reference:

Heinz G, Peterson LJ, Johnson RW, Kerk CJ. 2003. Exploring Relationships in Body Dimensions. Journal of Statistics Education 11(2).

Draw a normal probability plot of this data.

1. Order the numbers from smallest to largest number.

12.9 13.0 13.0 13.0 13.2 13.2 13.2 13.2 13.4 13.8 13.8 13.9 13.9 14.0 14.0 14.0 14.0 14.0 14.1 14.1 14.1 14.2 14.4 14.4 14.4 14.4 14.5 14.5 14.6 14.7 14.7 14.8 14.8 14.9 14.9 14.9 15.0 15.0 15.0 15.0 15.1 15.1 15.2 15.3 15.3 15.4 15.4 15.4 15.4 15.5 15.6 15.8 16.0 16.0 16.0 16.0 16.2 16.3 16.4 16.5.

2. Assign a rank to each value of your data.

diameter	rank
12.9	1
13.0	2
13.0	3
13.0	4
13.2	5
13.2	6
13.2	7
13.2	8
13.4	9
13.8	10
13.8	11
13.9	12
13.9	13
14.0	14
14.0	15
14.0	16
14.0	17
14.0	18
14.1	19
14.1	20
14.1	21
14.2	22
14.4	23
14.4	24
14.4	25
14.4	26
14.5	27
14.5	28
14.6	29
14.7	30
14.7	31
14.8	32
14.8	33
14.9	34
14.9	35
14.9	36
15.0	37
15.0	38
15.0	39
15.0	40
15.1	41
15.1	42
15.2	43
15.3	44
15.3	45
15.4	46
15.4	47
15.4	48
15.4	49
15.5	50
15.6	51
15.8	52
16.0	53
16.0	54
16.0	55
16.0	56
16.2	57
16.3	58
16.4	59
16.5	60

Note that repeated values or ties are ranked sequentially as usual.

The first (smallest) value is 12.9 cm so its rank is 1, the next value is 13.0 cm so its rank is 2.

The last (largest) value is 16.5 so its rank is 60.

3. Calculate the cumulative probability (pi) associated with each rank (I).

Since the number of data points = 60 which is larger than 10, so the formula reduces to:

pi=(i-0.5)/n

The following table will be produced:

diameter	rank	pi
12.9	1	0.008
13.0	2	0.025
13.0	3	0.042
13.0	4	0.058
13.2	5	0.075
13.2	6	0.092
13.2	7	0.108
13.2	8	0.125
13.4	9	0.142
13.8	10	0.158
13.8	11	0.175
13.9	12	0.192
13.9	13	0.208
14.0	14	0.225
14.0	15	0.242
14.0	16	0.258
14.0	17	0.275
14.0	18	0.292
14.1	19	0.308
14.1	20	0.325
14.1	21	0.342
14.2	22	0.358
14.4	23	0.375
14.4	24	0.392
14.4	25	0.408
14.4	26	0.425
14.5	27	0.442
14.5	28	0.458
14.6	29	0.475
14.7	30	0.492
14.7	31	0.508
14.8	32	0.525
14.8	33	0.542
14.9	34	0.558
14.9	35	0.575
14.9	36	0.592
15.0	37	0.608
15.0	38	0.625
15.0	39	0.642
15.0	40	0.658
15.1	41	0.675
15.1	42	0.692
15.2	43	0.708
15.3	44	0.725
15.3	45	0.742
15.4	46	0.758
15.4	47	0.775
15.4	48	0.792
15.4	49	0.808
15.5	50	0.825
15.6	51	0.842
15.8	52	0.858
16.0	53	0.875
16.0	54	0.892
16.0	55	0.908
16.0	56	0.925
16.2	57	0.942
16.3	58	0.958
16.4	59	0.975
16.5	60	0.992

4. Calculate the Z-score for each pi value using the function qnorm of the R programming language.

diameter	rank	pi	zi
12.9	1	0.008	-2.41
13.0	2	0.025	-1.96
13.0	3	0.042	-1.73
13.0	4	0.058	-1.57
13.2	5	0.075	-1.44
13.2	6	0.092	-1.33
13.2	7	0.108	-1.24
13.2	8	0.125	-1.15
13.4	9	0.142	-1.07
13.8	10	0.158	-1.00
13.8	11	0.175	-0.93
13.9	12	0.192	-0.87
13.9	13	0.208	-0.81
14.0	14	0.225	-0.76
14.0	15	0.242	-0.70
14.0	16	0.258	-0.65
14.0	17	0.275	-0.60
14.0	18	0.292	-0.55
14.1	19	0.308	-0.50
14.1	20	0.325	-0.45
14.1	21	0.342	-0.41
14.2	22	0.358	-0.36
14.4	23	0.375	-0.32
14.4	24	0.392	-0.27
14.4	25	0.408	-0.23
14.4	26	0.425	-0.19
14.5	27	0.442	-0.15
14.5	28	0.458	-0.11
14.6	29	0.475	-0.06
14.7	30	0.492	-0.02
14.7	31	0.508	0.02
14.8	32	0.525	0.06
14.8	33	0.542	0.11
14.9	34	0.558	0.15
14.9	35	0.575	0.19
14.9	36	0.592	0.23
15.0	37	0.608	0.27
15.0	38	0.625	0.32
15.0	39	0.642	0.36
15.0	40	0.658	0.41
15.1	41	0.675	0.45
15.1	42	0.692	0.50
15.2	43	0.708	0.55
15.3	44	0.725	0.60
15.3	45	0.742	0.65
15.4	46	0.758	0.70
15.4	47	0.775	0.76
15.4	48	0.792	0.81
15.4	49	0.808	0.87
15.5	50	0.825	0.93
15.6	51	0.842	1.00
15.8	52	0.858	1.07
16.0	53	0.875	1.15
16.0	54	0.892	1.24
16.0	55	0.908	1.33
16.0	56	0.925	1.44
16.2	57	0.942	1.57
16.3	58	0.958	1.73
16.4	59	0.975	1.96
16.5	60	0.992	2.41

5. Create an x-y scatter plot of your z-score values on the x-axis versus their corresponding data points on the y-axis.

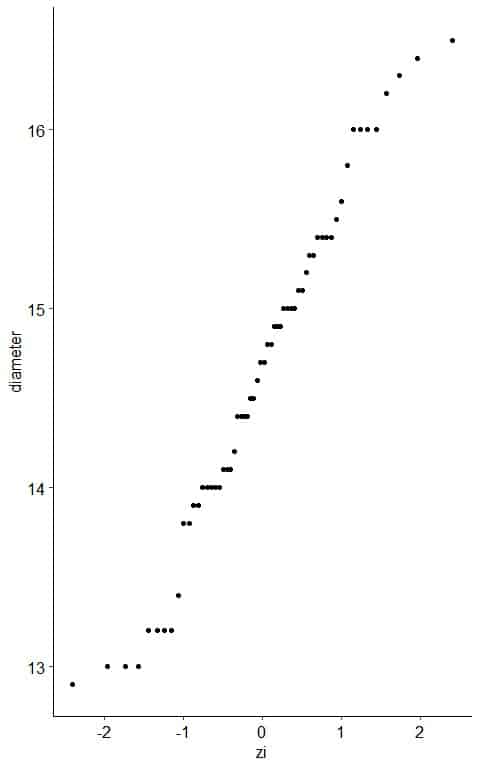6. If the diameter data are consistent with the normal percentiles from a normal distribution, the points should lie close to a straight line.

As a reference, a straight line is plotted which passes through the first and third quartiles.

From the table, we see that the first quartile (at pi = 0.25) was about 14.0 cm and zi = -0.65 and third quartile (at pi = 0.75) was 15.4 cm and zi = 0.70.

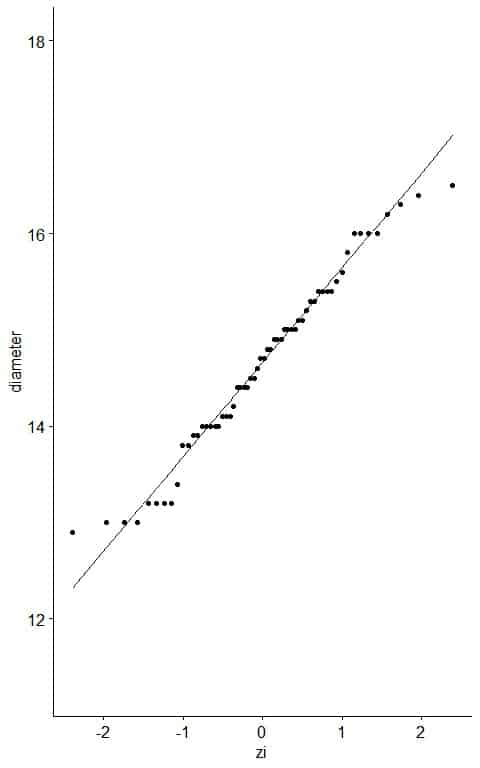
Nearly all the data are on the straight line, so it is normally distributed data.

3. How to read a normal probability plot?

The shape of a normal probability plot can tell you the distribution of your data.

– Example 1: normally-distributed variable

The following plot is the histogram and normal probability plot for heights in cm of 100 individuals.

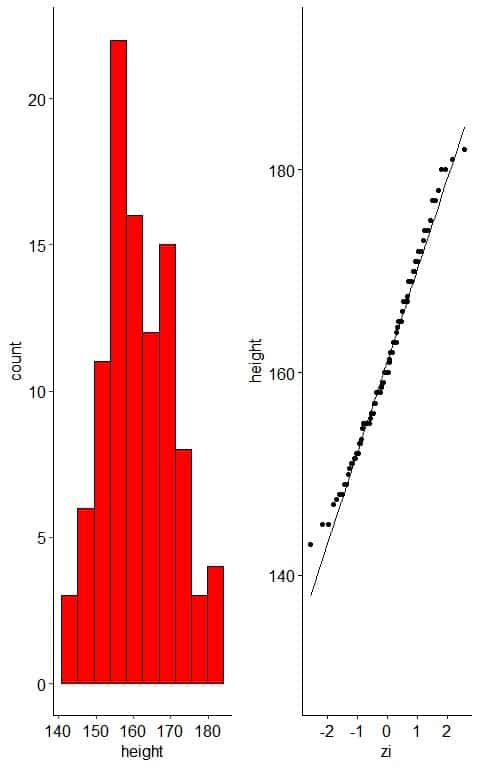
When the data is normally distributed, the histogram is nearly symmetric, unimodal, and bell-shaped.

The normal probability plot of normally distributed data will show nearly all the points on the reference straight line, at least when the few large and small values are ignored.

– Example 2: normally-distributed variable with one outlier

The following plot is the histogram and normal probability plot for heights in cm of 100 individuals.

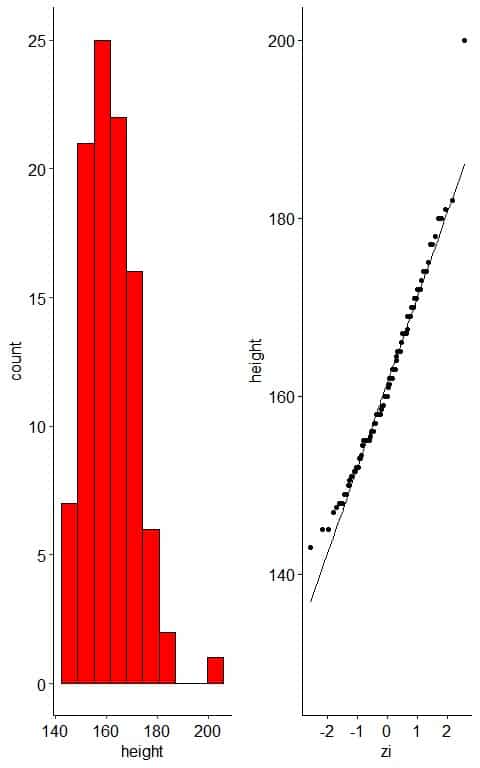
The histogram of the data will be the same except for a faraway bin for the outlier.

The normal probability plot will show that nearly all the points are near the straight line except the far away outlier point.

– Example 3: Right-skewed variable

The following plot is the histogram and normal probability plot for the Annual income of 100 individuals.

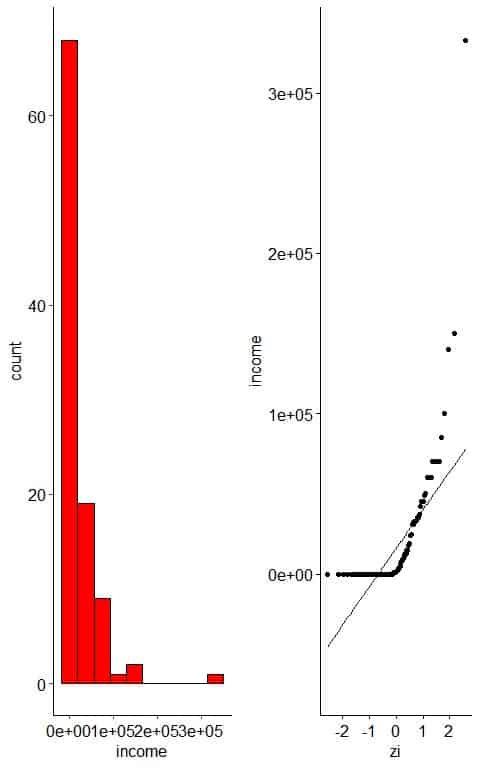
The histogram of right-skewed data looks unimodal with less frequent large values.

The normal probability plot of right-skewed data has an inverted C shape.

– Example 4: Left-skewed variable

The following plot is the histogram and normal probability plot for the Physical ability Lawyers’ ratings of state judges in the US Superior Court.

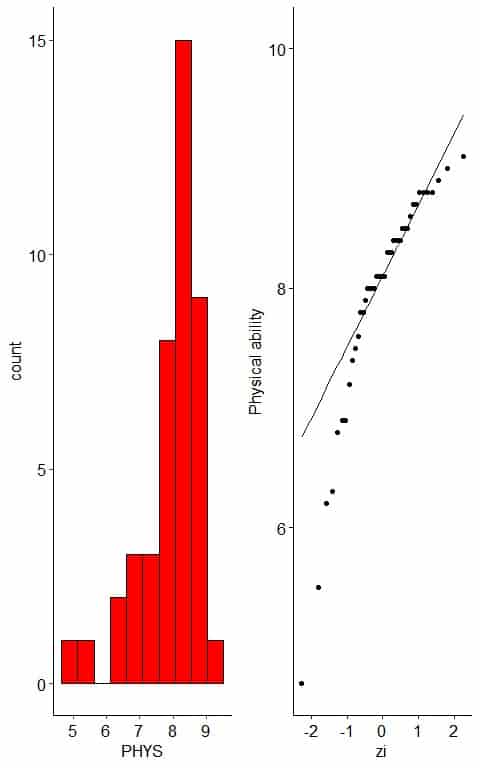
The histogram of left-skewed data looks unimodal with less frequent small values.

The normal probability plot of left-skewed data has a nearly C shape.

4. Practice questions

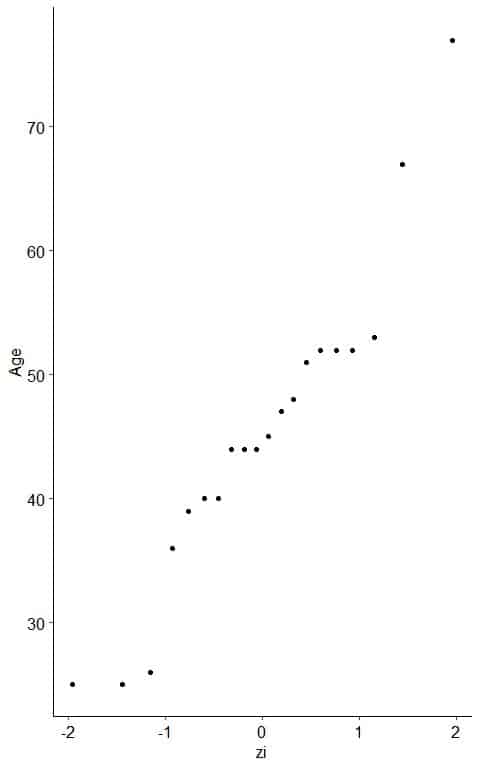
1. The following is the age in years for 20 participants from a certain survey.

26 48 67 39 25 25 36 44 44 47 53 52 52 51 52 40 77 44 40 45.

Draw a normal probability plot of this data.

2. The following normal probability plots for the weights (in kg) of males and females from a certain survey.

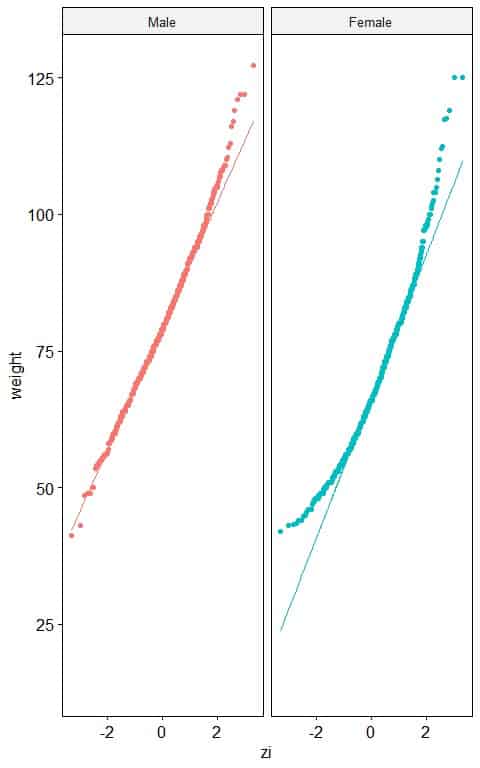Which sex has a normally distributed weight?

3. The following normal probability plots for the total cholesterol (in mg/dl) of different smoking statuses from a certain survey.

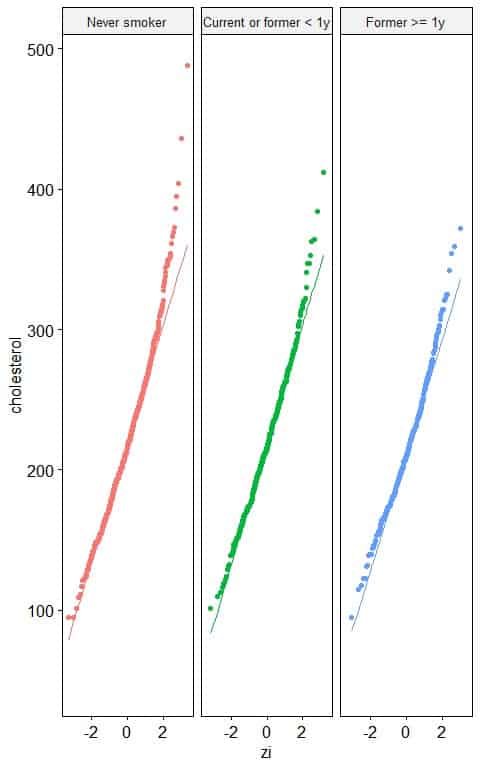Which smoking status has a normally distributed total cholesterol level?

4. The following normal probability plots for the annual income (in USD) of different employment statuses from a certain survey.

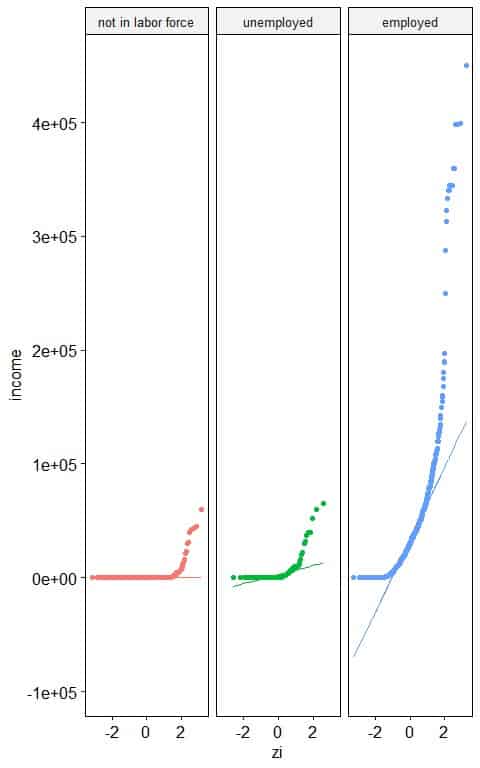
Which employment status has a normally distributed annual income?

5. The following normal probability plots for the air pressure (in millibars) of different storm classes (status).

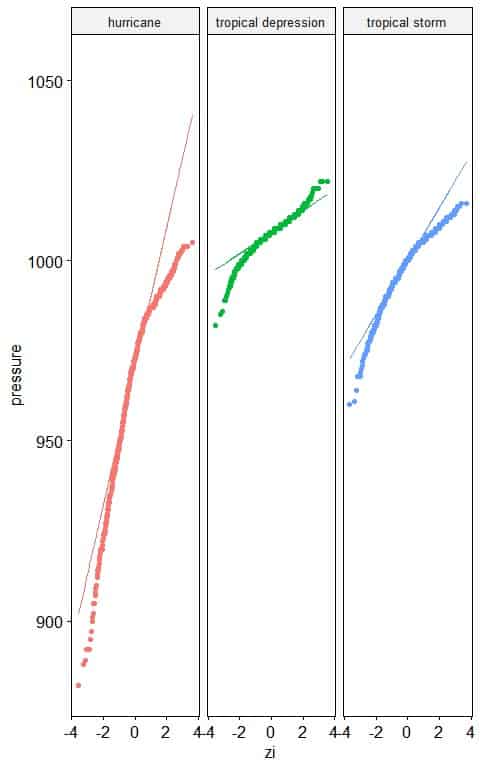
Which storm class has a normally distributed pressure?

5. Answer key

1. Order the numbers from smallest to largest number.

25 25 26 36 39 40 40 44 44 44 45 47 48 51 52 52 52 53 67 77.

Assign a rank to each value of your data.

Age	rank
25	1
25	2
26	3
36	4
39	5
40	6
40	7
44	8
44	9
44	10
45	11
47	12
48	13
51	14
52	15
52	16
52	17
53	18
67	19
77	20

Calculate the cumulative probability (pi) associated with each rank (I).

Since the number of data points = 20 which is larger than 10, so the formula reduces to:

pi=(i-0.5)/n

The following table will be produced:

Age	rank	pi
25	1	0.025
25	2	0.075
26	3	0.125
36	4	0.175
39	5	0.225
40	6	0.275
40	7	0.325
44	8	0.375
44	9	0.425
44	10	0.475
45	11	0.525
47	12	0.575
48	13	0.625
51	14	0.675
52	15	0.725
52	16	0.775
52	17	0.825
53	18	0.875
67	19	0.925
77	20	0.975

Calculate the Z-score for each pi value.

Age	rank	pi	zi
25	1	0.025	-1.96
25	2	0.075	-1.44
26	3	0.125	-1.15
36	4	0.175	-0.93
39	5	0.225	-0.76
40	6	0.275	-0.60
40	7	0.325	-0.45
44	8	0.375	-0.32
44	9	0.425	-0.19
44	10	0.475	-0.06
45	11	0.525	0.06
47	12	0.575	0.19
48	13	0.625	0.32
51	14	0.675	0.45
52	15	0.725	0.60
52	16	0.775	0.76
52	17	0.825	0.93
53	18	0.875	1.15
67	19	0.925	1.44
77	20	0.975	1.96

Create an x-y scatter plot of your z-score values on the x-axis versus their corresponding data points on the y-axis.

As a reference, a straight line can be added to the plot which passes through the first and third quartiles.

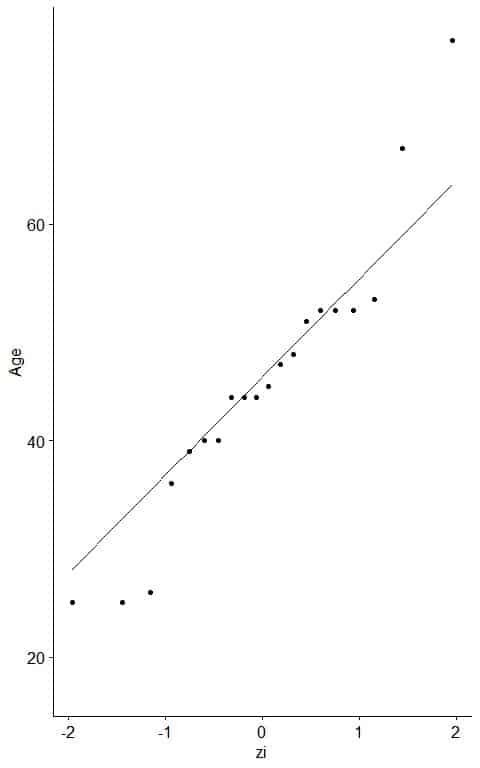
Nearly all the points on the straight line except small and large values, so it is nearly normally distributed data.

2. Males have nearly normally distributed weights as nearly all the points are along the straight line.

In females, the normal probability plot shows an inverted C shape which means that the female weights are right-skewed.

3. All the smoking statuses have nearly normally distributed total cholesterol levels as nearly all the points are along the straight line, except for small and large values.

4. “not in labor force” and “unemployed” statuses have nearly normally distributed annual income as nearly all the points are along the straight line, except for large values.

“employed” status has right-skewed annual income as the normal probability plot takes an inverted C-shape.

5. Tropical depression storms have nearly normally distributed pressure as nearly all the points are along the straight line, except for large and small values.

Hurricane and tropical storms have left-skewed pressure values as the normal probability plot takes a C-shape.

Normal Probability Plot – Explanation & Examples

1. What is a normal probability plot?

2. How to make a normal probability plot?

– Example 1

– Example 2

3. How to read a normal probability plot?

– Example 1: normally-distributed variable

– Example 2: normally-distributed variable with one outlier

– Example 3: Right-skewed variable

– Example 4: Left-skewed variable

4. Practice questions

5. Answer key

Previous Lesson | Main Page | Next Lesson