Opposite Adjacent Hypotenuse – Explanation & Examples

The terms opposite, adjacent, and hypotenuse are called the lengths of sides of a right triangle. A right triangle is considered to be one of the most powerful figures in Mathematics. We can easily solve complex real word problems if we know how to figure out the deep relation of the sides of a right triangle.

The terms hypotenuse, adjacent, opposite are used to represent the sides of a right triangle. The building block expertise in Trigonometry is being able to discuss and solve different sides of a right-angled triangle deeply related to each other to solve real-world problems.

Can you imagine finding the height of the world’s tallest tower — Burj Khalifa — while standing on the ground at a certain distance from it? One idea is to make an estimated guess, but a better approach to finding the height is by using the knowledge of the right-angled triangle. If you just know the approximate angle the tower makes with the ground, you can determine the height of the Burj Khalifa while standing on the ground.

Just imagine, with just two pieces of information — the distance on the ground and the approximate angle the tower makes with the ground — you can achieve the otherwise impossible. But how? That’s exactly what we will try to learn in trigonometry using the right triangles. This is why right triangles are one of the most influential concepts in Mathematics.

After studying this lesson, we are expected to learn the concepts driven by the following questions and be qualified to address accurate, specific, and consistent answers to these questions.

• How do you find the adjacent, hypotenuse, and opposite sides of the right triangle?
• What is the opposite side of the right triangle?
• What is the adjacent side of the right triangle?
• How do the different sides (hypotenuse, adjacent, opposite) of a triangle deeply related to each other?
• How can we solve real-world problems using the right triangle?

This lesson aims to clear up any confusion you might have about the concepts involving right triangles.

How do you find the adjacent, hypotenuse, and opposite sides of the right triangle?

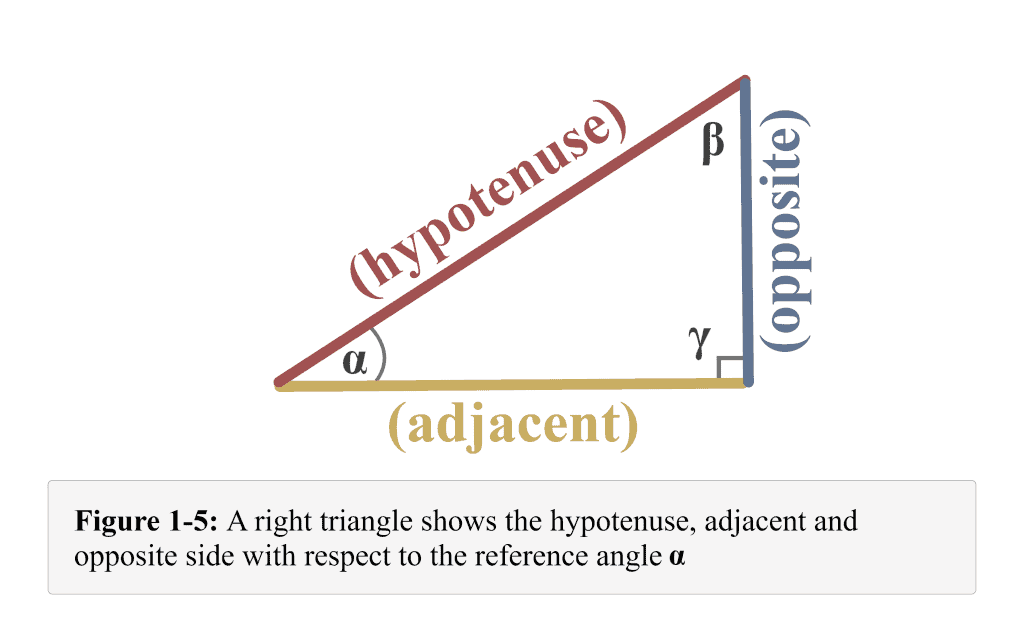
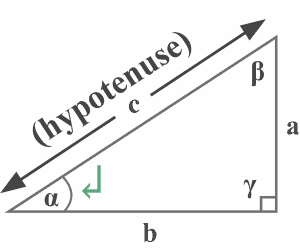
A triangle is referred to as a right triangle in which one of the interior angles is a right angle — measures $90^{\circ }$. The following Figure 1-1 represents a typical right triangle. The lengths of the three legs (sides) of the right triangle are named $a$, $b$, and $c$. The angles opposite the legs of lengths $a$, $b$, and $c$ are named $\alpha$, $\beta$, and $\gamma$. The tiny square designated to the angle $\gamma$ shows that it is a right angle.

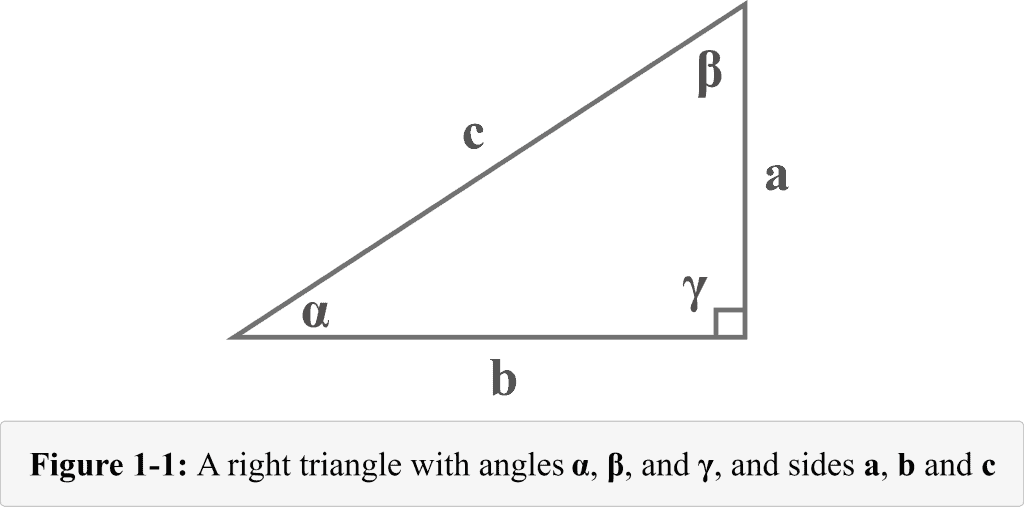
A common practice is that a triangle is labelled in terms of naming the sides with lowercase letters and the angles (vertices) opposite the sides with corresponding small letters. 

The following diagram 1-2 represents the hypotenuse — the longest side — of a right-angled triangle. It is clear from the diagram that the hypotenuse of a right-angled triangle is opposite to the right angle $\gamma$. That side one will always remain the hypotenuse independent of what angle we are looking at because it is a unique side. 

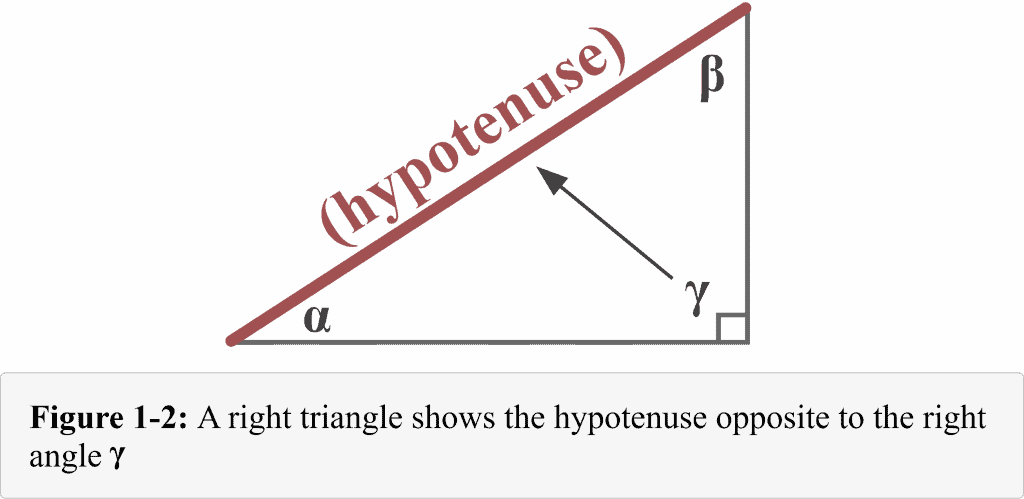
The other two sides — adjacent and the opposite — are named with respect to the reference angle’s location. Please make sure you recognize clearly how the legs of the triangles are labeled.

The following diagram 1-3 represents the adjacent side. It is clear from the diagram that the adjacent side of a right-angled triangle is right next to the reference angle $\alpha$.

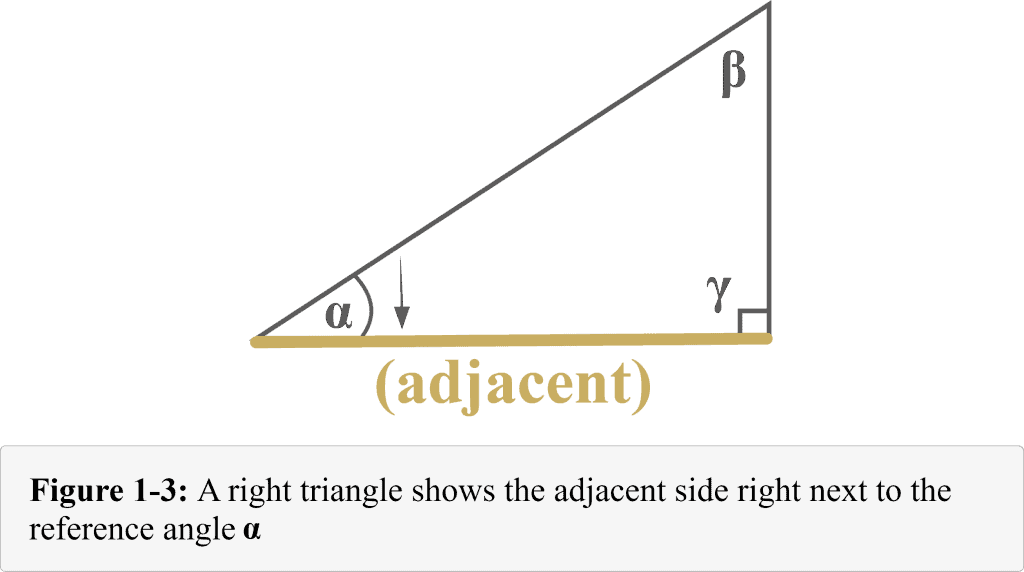
The following diagram 1-4 represents the opposite side all the way across the other side from the reference angle $\alpha$. It is clear from the diagram that the opposite side of a right-angled triangle lies exactly opposite to the reference angle $\alpha$.

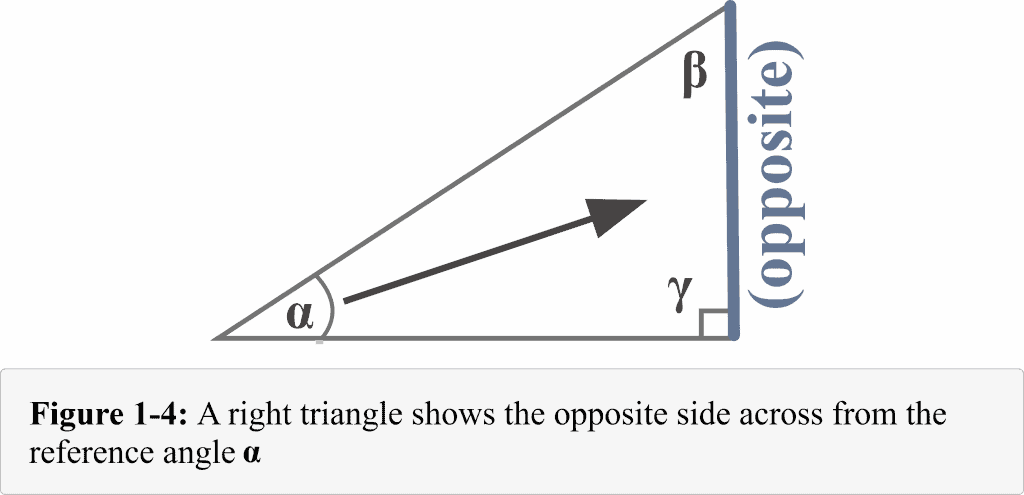
Combining all concerning the reference angle $\alpha$, we get the illustration shown in Figure 1-5.

For example, using the right-angled triangle shown in the below figure to determine the opposite, adjacent, and the hypotenuse of the right triangle with respect to the angle $\alpha%%EDITORCONTENT%%nbsp;as shown below.

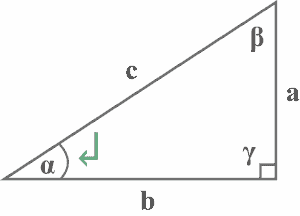
The opposite side of a right triangle

Looking at the above diagram, the side $a%%EDITORCONTENT%%nbsp;lies exactly opposite to the reference angle $\alpha$. Thus, $a$ is the opposite side of the right triangle with respect to the reference angle $\alpha$, as shown below.

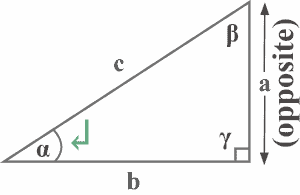
The adjacent side of a right triangle

It is clear from the same diagram that the side $b%%EDITORCONTENT%%nbsp;is right next to the reference angle α. Thus, $b$ is the adjacent side of the right triangle with respect to the reference angle $\alpha$, as shown below.

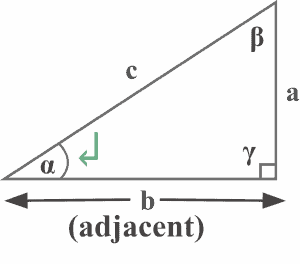
The hypotenuse of a right triangle

The diagram also clearly shows that the side $c$ is opposite to the right angle $\gamma$. Thus, $c$ is the hypotenuse of the right triangle, as shown below.

The relationship between the right triangle and the Pythagorean Theorem

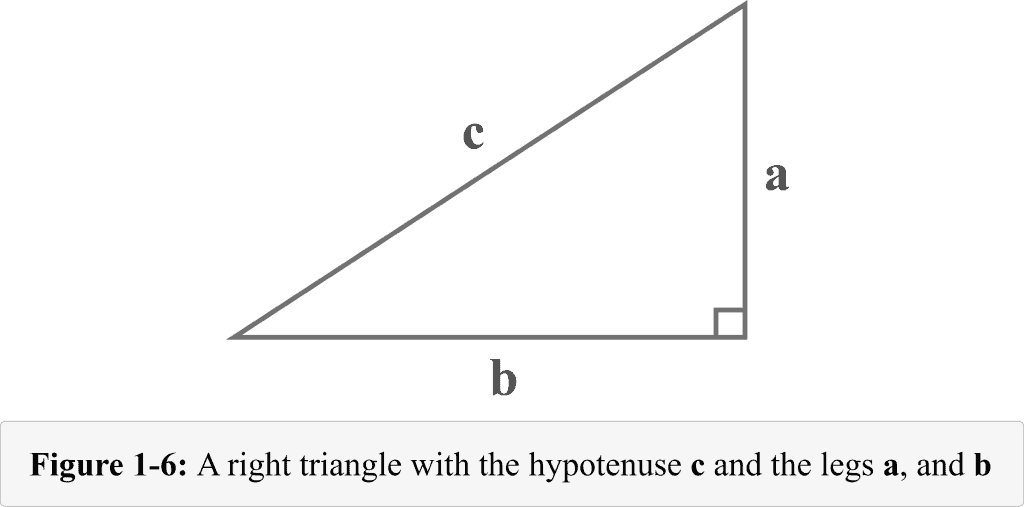
The Pythagoras theorem is one of the most powerful concepts in Mathematics. We need to draw the right triangle to understand this concept. Figure 1-6 represents a simple right-angled triangle with the sides $a$, $b$, and $c$.

What’s so unique about this triangle or this theorem?

The Pythagoras theorem states that the hypotenuse has a particular relationship with the other two legs. It says that the square of the hypotenuse is equal to the sum of squares of the other two sides. We must not forget that it is valid only in the case of a right triangle.

The diagram shows that the length $c$ is the hypotenuse of the right triangle. According to the Pythagoras theorem, the hypotenuse, $c$, of a right triangle is associated with the other sides, $a$, and $b$.

$c^{2}=a^{2}+b^{2}$

Using the Pythagoras theorem, we can solve numerous real word problems.

For example:

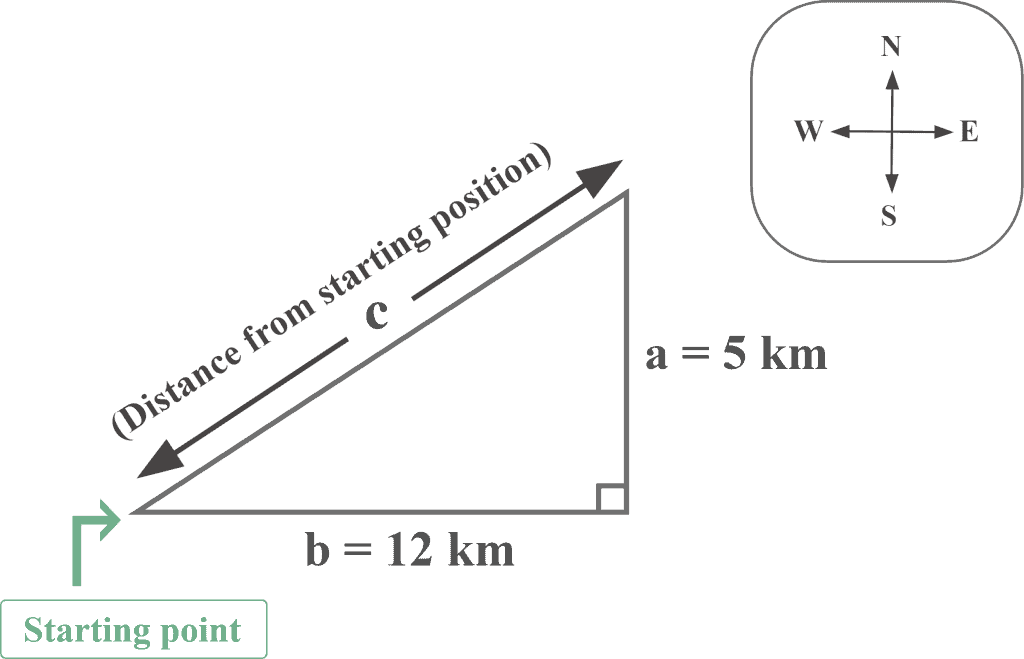
Let suppose Mr. Tony walks $12$ kilometers East and then $5$ kilometers north. Determine how far is he away from his starting position?

Step $1$: Draw a diagram

Step $2$: Set up an equation and solve

The diagram clearly shows that it involves a right triangle. Here:

The distance covered towards East $= b = 12$ km

The distance covered towards North $= a = 5$ km

We have to determine the hypotenuse, $c$, to find how far Mr. Tony away from his starting position. Thus, using the Pythagoras theorem

$c^{2}=a^{2}+b^{2}$

$c^{2}=5^{2}+12^{2}$

$c^{2}=25+144$

$c^{2}=169$

$c = 13$ km

Thus, Mr. Tony is $13$ kilometers away from his starting position

Example $1$

Given the right triangle $XYZ$, which side is adjacent with respect to the reference angle $X$?

Solution:

It is clear from the diagram the side $XZ%%EDITORCONTENT%%nbsp;is right next to the reference angle $X$. Thus, $XZ$ is the adjacent side of the right triangle $XYZ$ with respect to the reference angle $X$.

Example $2$

Given the right triangle $PQR$, which side is the opposite with respect to the reference angle $P$?

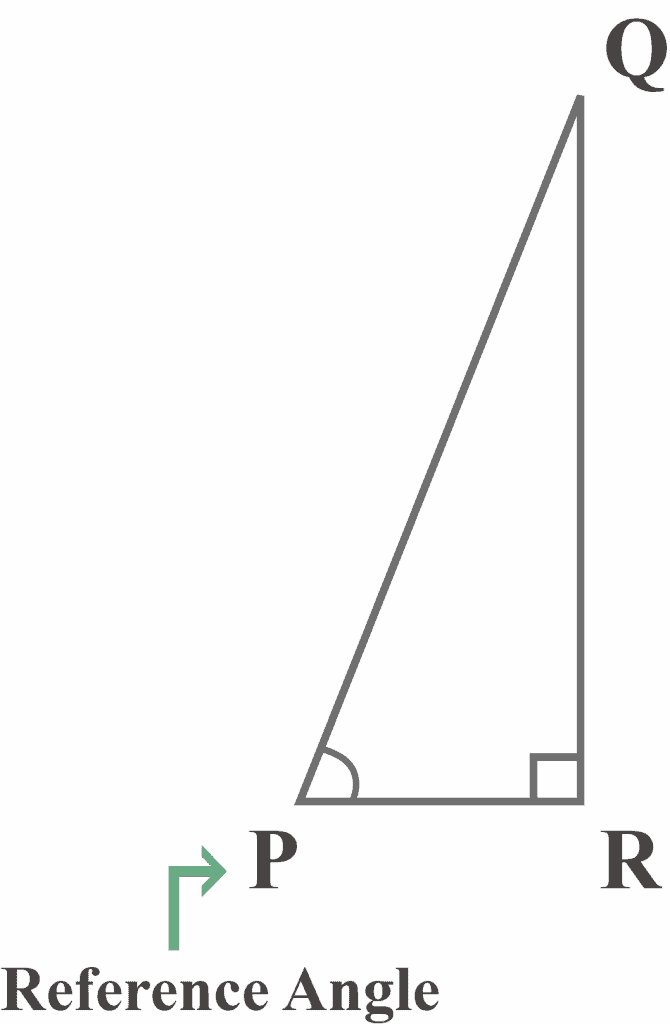
From the diagram the side $QR$ lies exactly opposite to the reference angle $P$. Thus, $QR$ is the opposite side of the right triangle $PQR$ with respect to the reference angle $P$.

Example $3$

Given the right triangle $LMN$, which side is the hypotenuse?

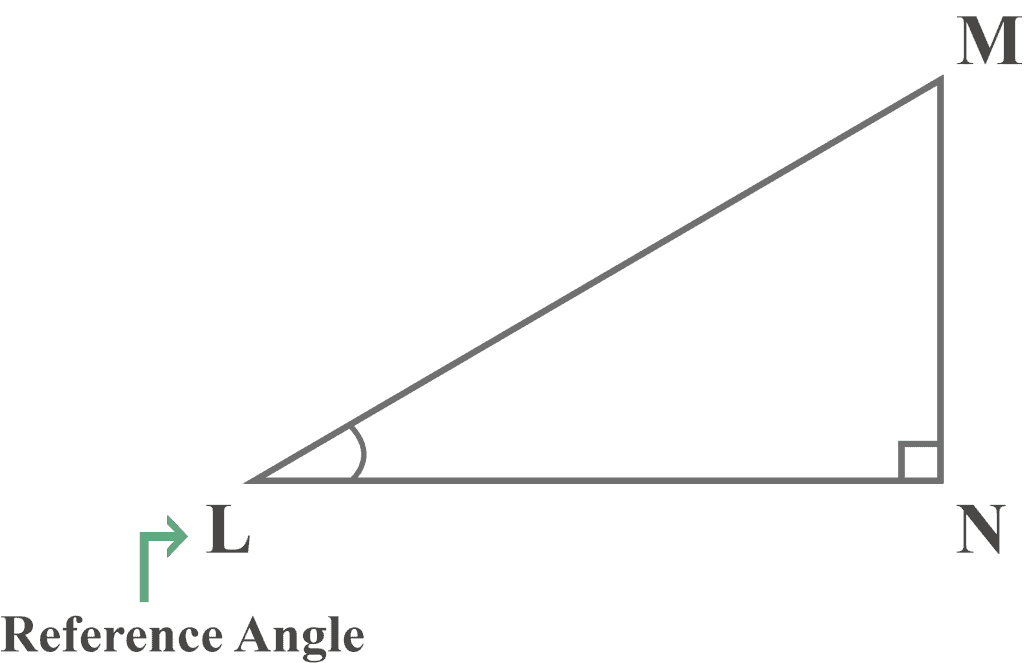
Solution:

Looking at the above diagram, $∠N$ is a right angle.

Also, the side $LM$ is opposite to the right angle $N$. Thus, $LM$ is the hypotenuse of the right triangle $LMN$.

Example $4$

Given the right triangle, determine

        $1$. the opposite 

       $2$. the adjacent

       $3$. the hypotenuse

of a right triangle with respect to the angle $\alpha$.

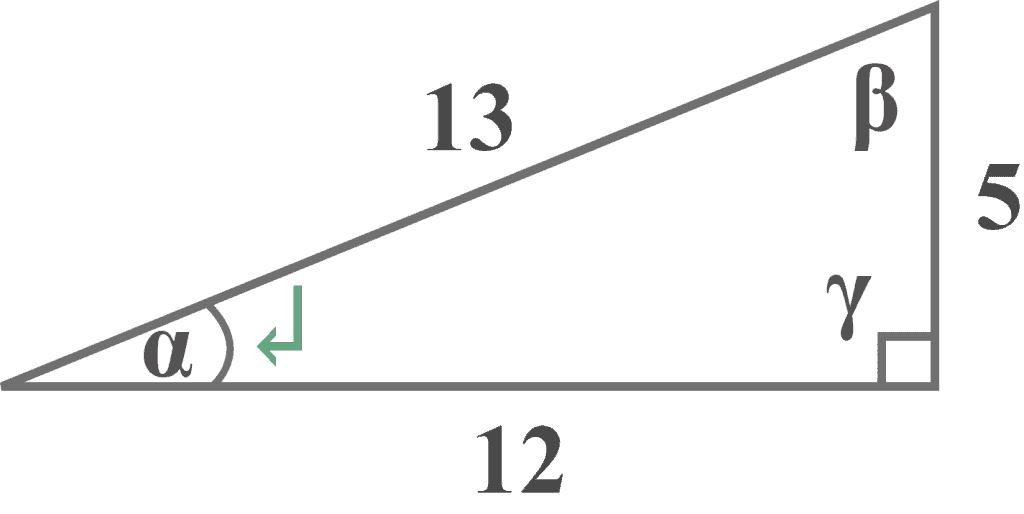
Solution:

       $1$. The opposite

Looking at the above diagram, the angle $\gamma$ is a right angle.

It is clear that the side $5%%EDITORCONTENT%%nbsp;lies exactly opposite to the reference angle $\alpha$.

Thus,

The opposite side = $5$ units

       $2$. The adjacent

It is clear that the side $12%%EDITORCONTENT%%nbsp;is right next to the reference angle $\alpha$.

Thus,

The adjacent side = $12$ units

       $3$. The hypotenuse

The diagram clearly shows that the side $13$ is opposite to the right angle $\gamma$.

Thus,

The hypotenuse = $13$ units