- Home
- >
- Parametric equations – Explanation and Examples
JUMP TO TOPIC
Parametric Equation – Explanation and Examples
 In mathematics, a parametric equation is explained as:
In mathematics, a parametric equation is explained as:
“A form of the equation that has an independent variable in terms of which any other equation is defined, and dependent variables involved in such an equation are continuous functions of the independent parameter.”
For instance, let us consider the equation of a parabola. Instead of writing it in the cartesian form that is y = x2 we can write it in parametric form, which is stated as follow,
x = t
y = t2
where “t” is an independent variable called a parameter.
In this topic, we will cover the following points in detail:
- What is a parametric equation?
- Examples of parametric equations
- Parametrization of curves?
- How to write a parametric equation?
- How to graph various parametric equations?
- Understanding with the help of examples.
- Problems
What Is A Parametric Equation?
A parametric equation is a form of the equation that has an independent variable called a parameter, and other variables are dependent on it. There can be more than when dependent variables, but they do not depend on each other.
It is important to note that parametric equation representations are not unique; hence, the same quantities can be expressed in several ways. Similarly, parametric equations are not necessarily functions. The method of forming parametric equations is known as parameterization. Parametric equations are useful for representing and explaining curves such as circles, parabolas, etc., surfaces, and projectile motions.
To have a better understanding, let’s consider an example of our planetary system as the earth revolves around the sun in its orbit with some speed. At any instance, the earth is at some particular position relative to the other planets and sun. Now, a question arises; how we can write and solve the equations for describing the position of the earth when all the other parameters such as the speed of the earth in its orbit, distance from the sun, distance from other planets revolving in their particular orbits and many other factors, all are unknown. So, then parametric equations come into play as only one variable can be solved at a time.
Hence, in this case, we will use x(t) and y(t) as variables, where t is the independent variable, to determine the position of the earth in its orbit. Similarly, it can also help us detect the earth’s movement with respect to time.
Hence, parametric equations can be more particularly defined as:
“If x and y are continuous functions of t in any given interval, then the equations
x = x(t)
y = y(t)
are called parametric equations, and t is called an independent parameter.”
If we consider an object having a curvilinear motion in any given direction and at any instance of time. The motion of that object in the 2-D plane is described by x and y coordinates where both the coordinates are the function of time as they vary with time. For that reason, we expressed x and y equations in terms of another variable called a parameter upon which both x and y are dependent. So, we can classify x and y as dependent variables and t as an independent parameter.
Let’s again consider the earth analogy explained above. The position of the earth along the x-axis is represented as x(t). The position along the y-axis is represented as y(t). Together, both these equations are called parametric equations.
Parametric equations give us more information about position and direction with respect to time. Several equations cannot be represented in the form of functions, so we parametrize such equations and write them in terms of some independent variable.
For instance, let us consider the equation of the circle that is:
x2 + y2 = r2
the parametric equations of a circle are given as:
x = r.cosθ
y = r.sinθ
Let us have a better understanding of the above-explained concept with the help of an example.
Example 1
Write down the following mentioned rectangular equations into parametric form
- y = 3x3 + 5x +6
- y = x2
- y = x4 + 5x2 +8
Solution
Let’s evaluate the equation 1:
y = 3x3 + 5x +6
Following steps must be followed in order to convert the equation in parametric form
For parametric equations,
Put x = t
So, the equation becomes,
y = 3t3 + 5t + 6
The parametric equations are given as,
x = t
y = 3t3 + 5t + 6
Now consider the equation 2:
y = x2
Following steps must be followed in order to convert the equation in parametric form
Let’s put x = t
So, the equation becomes,
y = t2
The parametric equations are given as,
x = t
y = t2
Let us solve for the equation 3:
y = x4 + 5x2 +8
Following steps must be followed in order to convert the equation in parametric form
Putting x = t,
So, the equation becomes,
y = t4 + 5t2 + 8
The parametric equations are given as,
x = t
y = t4 + 5t2 + 8
How To Write A Parametric Equation?
We will understand the procedure of parametrization with the help of an example.Consider an equation y = x2 + 3x +5. To parametrize the given equation, we will follow the following steps :
- First of all, we will assign any one of the variables involved in the above equation equals to t. Let’s say x = t
- Then the above equation will become y = t2 + 3t + 5
- So, the parametric equations are: x = t y(t) = t2 + 3t + 5
Hence, it is useful to convert rectangular equations into parametric form. It helps to plot and is easy to understand; therefore, it generates the same graph as a rectangular equation but with better understanding. This conversion is sometimes necessary as some of the rectangular equations are very complicated and difficult to plot, so converting them into parametric equations and vice versa makes it easier to solve. This kind of conversion is referred to as “eliminating the parameter.” To rewrite the parametric equation in the form of a rectangular equation, we are trying to develop a relationship between x and y whereas eliminating t.
For example, if we want to write a parametric equation of the line that passes through point A (q, r, s) and is parallel to the direction vector v <v1, v2, v3>.
The equation of the line is given as:
A = A0 + tv
where A0 is given as the position vector pointing towards point A(q, r, s) and is denoted as A0 <q, r, s>.
So, putting in the equation of line gives,
A = <q, r, s> + t<v1, v2, v3>
A = <q, r, s> + <tv1, tv2, tv3>
Now, adding respective components gives,
A = 1,r + tv2, s + tv3>
Now, for the parametric equation, we will consider each component.
So, the parametric equation is given as,
x = q + tv1
y = r + tv2
z = s + tv3
Example 2
Find out the parametric equation of a parabola (x – 3) = -16(y – 4).
Solution
The given parabolic equation is:
(x – 3) = -16(y – 4) (1)
Let us compare the above parabolic mentioned equation with the standard equation of a parabola that is:
x2 = 4ay
and the parametric equations are,
x = 2at
y = at2
Now, comparing the standard equation of a parabola with the given equation which gives,
4a = -16
a = -4
So, putting the value of a in the parametric equation gives,
x = -8t
y = -4t2
Since the given parabola is not centered at the origin, it is located at point (3, 4) so, further comparison gives,
x – 3 = -8t
x = 3 – 8t
y – 4 = -4t2
y = 4 – 4t2
So, the parametric equations of the given parabola are,
x = 3 – 8t
y = 4 – 4t2
Eliminating The Parameter in Parametric Equations
As we have already explained above, the concept of eliminating parameters. This is another technique of tracing a parametric curve. This will result in an equation involving a and y variables. For example, as we have defined the parametric equations of a parabola as,
x = at (1)
y = at2 (2)
Now, solving for t gives,
t = x/a
Substitute value of t eq (2) will yield the value of y, that is,
y = a(x2/a)
y = x2
and it is the rectangular equation of a parabola.
It is easier to draw a curve if the equation involves only two variables: x and y. Hence, eliminating the variable is a method that simplifies the process of graphing curves. However, if we are required to graph the equation with correspondence to time, then the curve’s orientation must be defined. There are many ways to eliminate the parameter from the parametric equations, but not all the methods can solve all the problems.
One of the most common methods is to choose the equation among the parametric equations that can be most easily resolved and manipulated. Then we will find out the value of independent parameter t and substitute it in the other equation.
Let’s have a better understanding with the help of an example.
Example 3
Write down the following parametric equations in the form of cartesian equation
- x(t) = t2 – 1 and y(t) = 2 – t
- x(t) = 16t and y(t) = 4t2
Solution
Consider equation 1
x(t) = t2 – 1 and y(t) = 2 – t
Consider the equation y(t) = 2 – t for finding out the value of t
t = 2 – y
Now, substitute the value t in equation x(t) = t2 – 1
x(t) = (2 – y)2 – 1
x = (4 – 4y + y2) – 1
x = 3 – 4y + y2
So, the parametric equations are converted into a single rectangular equation.
Now, consider the equation 2
x(t) = 16t and y(t) = 4t2
Consider the equation x(t) = 16t for finding out the value of t
t = x/16
Now, substitute the value t in equation y(t) = 4t2
y(t) = 4(x/16)2 – 1
y = 4( x2)/256 – 1
y =1/64 (x2 ) -1
So, the parametric equations are converted into a single rectangular equation.
To check whether the parametric equations are equivalent to the cartesian equation, we can check the domains.
Now, let’s talk about a trigonometric equation. We will use a substitution method, some trigonometric identities, and Pythagoras theorem to eliminate the parameter from a trigonometric equation.
Consider following parametric equations,
x = r.cos(t)
y = r.sin(t)
Let’s solve the above equations for the values of cos(t) and sin(t),
cos(t) = x/r
sin(t) = y/r
Now, using the trigonometric identity dives,
cos2(t) + sin2(t) = 1
Putting the values in the above equation,
(x/r)2 + (y/r)2 = 1
x2/r2 + y2/r2 = 1
x2 + y2 = 1.r2
x2 + y2 = r2
Hence, this is the rectangular equation of a circle. Parametric equations are not unique therefore there are a number of representations for parametric equations of a single curve.
Example 4
Eliminate the parameter from the given parametric equations and transform it into a rectangular equation.
x = 2.cos(t) and y = 4.sin(t)
Solution
Firstly, solve the above equations to find out the values of cos(t) and sin(t)
So,
cos(t) = x/2
sin(t) = y/4
Using the trigonometric identity that is stated as,
cos2(t) + sin2(t) = 1
(x/2)2 + (y/4)2 = 1
x2/4 + y2/16 = 1
Since, by looking into the equation we can identify this equation as the equation of an ellipse with center at (0, 0).
How To Graph Parametric Equations
Parametric curves can be plotted in the x-y plane by evaluating the parametric equations in the given interval. Any curve drawn in the x-y plane can be represented parametrically, and the resulting equations are called a parametric equation. Since we have already discussed above that x and y are continuous functions of t in a given interval I, then the resulting equations are,
x = x(t)
y = y(t)
These are called parametric equations, and t is called an independent parameter. The set of points (x, y) obtained in terms of t that varies in an interval is called the graph of parametric equations, and the resulting graph is the curve of parametric equations.
In the parametric equations, x and y are represented in terms of the independent variable t. As t varies over the given interval I, the function x(t) and y(t) generate a set of ordered pairs (x, y). Graph the set of the ordered pair that will generate the curve of parametric equations.
To graph the parametric equations, follow the steps explained below.
- First of all, identify the parametric equations.
- Construct a table having three columns for t, x(t), and y(t).
- Find out the values of x and y with respect to t over the given interval I in which the functions are defined.
- As a result, you will obtain a set of ordered pairs.
- Plot the resulting set of ordered pairs to obtain the parametric curve.
Note: We will use online software named GRAPHER to plot the parametric equations in the examples.
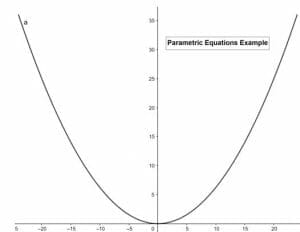
Example 5
Sketch the parametric curve of the following parametric equations
x(t) = 8t and y(t) = 4t2
Solution
Construct a table having three columns t, x(t), and y(t).
x(t) = 8t
y(t) = 4t2
| t | x(t) | y(t) |
| -3 | -24 | 36 |
| -2 | -16 | 16 |
| -1 | -8 | 4 |
| 0 | 0 | 0 |
| 1 | 8 | 4 |
| 2 | 16 | 16 |
| 3 | 24 | 36 |
So, the resulting graph sketched with the help of the software is given below,
Example 6
Sketch the parametric curve of the following parametric equations
x(t) = t + 2 and y(t) = √(t + 1) where t ≥ -1.
Solution
Construct a table having three columns for t, x(t), and y(t).
Given equations are,
x(t) = t + 2
y(t) = √(t + 1)
The table is shown below:
| t | x(t) | y(t) |
| -1 | 1 | 0 |
| 0 | 2 | 1 |
| 1 | 3 | 1.41 |
| 2 | 4 | 1.73 |
| 3 | 5 | 2 |
| 4 | 6 | 2.23 |
| 5 | 7 | 2.44 |
The graph of the parametric equation is given below:
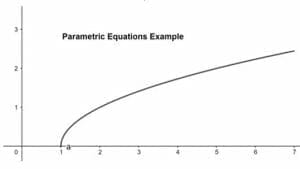
So, as we can see in that the domain of the function with t is restricted, we consider -1 and positive values of t.
Example 7
Eliminate the parameter and convert the given parametric equations into rectangular equations. Also, sketch the resulting rectangular equation and show the correspondence between both the parametric and rectangular equation of the curve.
x(t) = √(t + 4) and y(t) = t + 1 for -4 ≤ t ≤ 6.
Solution
In order to eliminate the parameter, consider the above parametric equations
x(t) = √(t + 4)
y(t) = t + 1
Using the equation of y(t), solve for t
t = y – 1
Hence, the value of the y will change as the interval is given as,
-4 ≤ t ≤ 6
-4 ≤ y – 1 ≤ 6
-3 ≤ y ≤ 7
Putting the value of t in equation of x(t)
x = √(y – 1 + 4)
x = √(y + 3)
So, this is the rectangular equation.
Now, construct a table having two columns for x and y,
| x | y |
| 0 | -3 |
| 1 | -2 |
| 1.41 | -1 |
| 1.73 | 0 |
| 2 | 1 |
| 2.23 | 2 |
| 2.44 | 3 |
| 2.64 | 4 |
The graph is shown below:
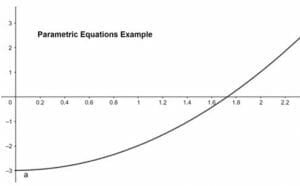
To show, let us draw the graph for the parametric equation.
Similarly, construct a table for parametric equations having three columns for t, x(t), and y(t).
| t | x(t) | y(t) |
| -4 | 0 | -3 |
| -3 | 1 | -2 |
| -2 | 1.41 | -1 |
| -1 | 1.73 | 0 |
| 0 | 2 | 1 |
| 1 | 2.23 | 2 |
| 2 | 2.44 | 3 |
| 3 | 2.64 | 4 |
The graph is given below:

So, we can see that both graphs are similar. Therefore, it is concluded that there exists a correspondence between two equations, i.e., Parametric equations and rectangular equations.
So, we can see that both graphs are similar. Therefore, it is concluded that there exists a correspondence between two equations, i.e., Parametric equations and rectangular equations.
Important Points To Note
Following are some important points to be noted:
- Parametric equations help to represent the curves that are not a function by splitting them into two parts.
- Parametric equations are non-unique.
- Parametric equations describe the complicated curves easily that are difficult to describe while using rectangular equations.
- Parametric equations can be converted into rectangular equations by eliminating the parameter.
- There are several ways to parametrize a curve.
- Parametric equations are very useful in solving real-world problems.
Practice Problems
- Write down the following mentioned rectangular equations into parametric form: y = 5x3 + 7x2 +4x + 2 y = -16x2 y = ln(x) + 1
- Find out the parametric equation of a circle given as (x – 2)2 + (y – 2)2 = 16.
- Find out the parametric equation of a parabola y = 16x2.
- Write down the following parametric equations in the form of cartesian equation x(t) = t + 1 and y(t) = √t.
- Eliminate the parameter from the given parametric equations of a trigonometric function and transform it into a rectangular equation. x(t) = 8.cos(t) and y(t) = 4.sin(t)
- Eliminate the parameter from the given parametric equations of a parabolic function and transformed into a rectangular equation. x(t) = -4t and y(t) = 2t2
- Sketch the parametric curve of the following parametric equations x(t) = t – 2 and y(t) = √(t) where t ≥ 0.
Answers
- x=t , y=5t3 + 7t2 +4t + 2 x=t, y=t2 x=t, y=ln(t) +1
- x=2 + 4cos(t), y = 2 + 4sin(t)
- x = 8t, y = 4t2
- y = √( x – 1 )
- x2 + 4y2 = 64
- x = 8y
Note: use the online software to sketch the parametric curve.
