Parent Functions – Types, Properties & Examples

When working with functions and their graphs, you’ll notice how most functions’ graphs look alike and follow similar patterns. That’s because functions sharing the same degree will follow a similar curve and share the same parent functions.

A parent function represents a family of functions’ simplest form.

This definition perfectly summarizes what parent functions are. We use parent functions to guide us in graphing functions that are found in the same family. In this article, we will:

• Review all the unique parent functions (you might have already encountered some before).
• Learn how to identify the parent function that a function belongs to.

Being able to identify and graph functions using their parent functions can help us understand functions more, so what are we waiting for?

What is a parent function?

Now that we understand how important it is for us to master the different types of parent functions let’s first start to understand what parent functions are and how their families of functions are affected by their properties.

Parent function definition

Parent functions are the simplest form of a given family of functions. A family of functions is a group of functions that share the same highest degree and, consequently, the same shape for their graphs.

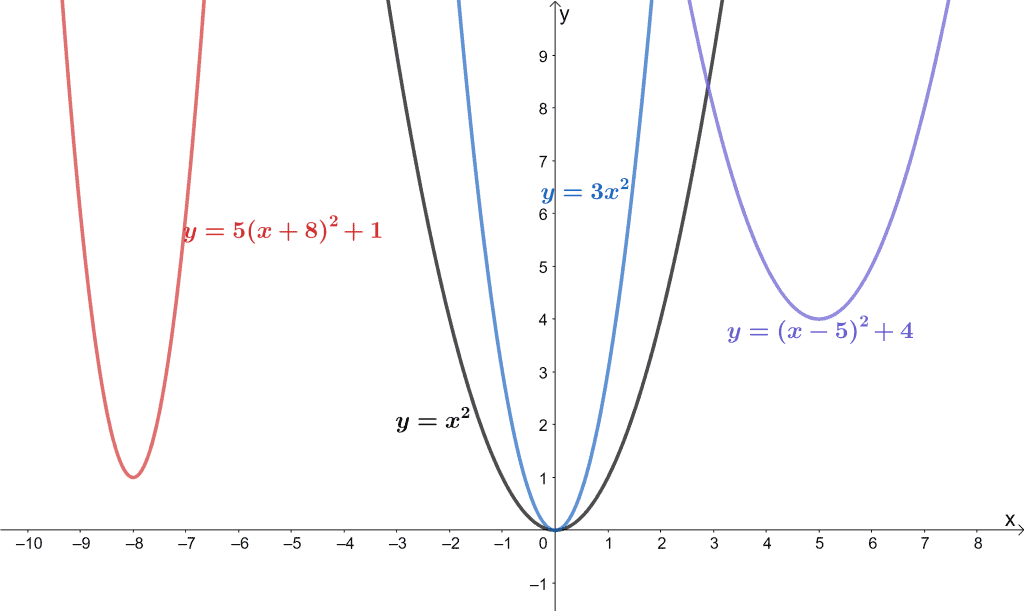
The graph above shows four graphs that exhibit the U-shaped graph we call the parabola. Since they all share the same highest degree of two and the same shape, we can group them as one family of function. Can you guess which family do they belong to?

These four are all quadratic functions, and their simplest form would be y = x². Hence, the parent function for this family is y = x².

Since parent functions are the simplest form of a given group of functions, they can immediately give you an idea of how a given function from the same family would look like.

What are the different types of parent functions?

It’s now time to refresh our knowledge about functions and also learn about new functions. As we have mentioned, familiarizing ourselves with the known parent functions will help us understand and graph functions better and faster.

Why don’t we start with the ones that we might already have learned in the past?

The first four parent functions involve polynomials with increasing degrees. Let’s observe how their graphs behave and take note of the respective parent functions’ domain and range.

Constant Functions

Constant functions are functions that are defined by their respective constant, c. All constant functions will have a horizontal line as its graph and contain only a constant as its term.

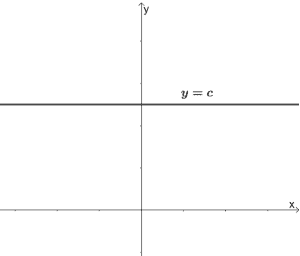
All constant functions will have all real numbers as its domain and y = c as its range. They also each have a y-intercept at (0, c).

An object’s motion when it is at rest is a good example of a constant function.

Linear Functions

Linear functions have x as the term with the highest degree and a general form of y = a + bx. All linear functions have a straight line as a graph.

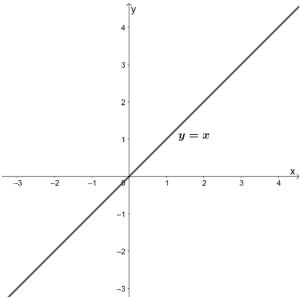
The parent function of linear functions is y = x, and it passes through the origin. The domain and range of all linear functions are all real numbers.

These functions represent relationships between two objects that are linearly proportional to each other.

Quadratic Functions

Quadratic functions are functions with 2 as its highest degree. All quadratic functions return a parabola as their graph. As discussed in the previous section, quadratic functions have y = x² as their parent function.

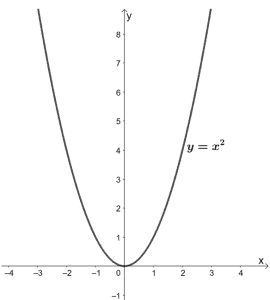
The vertex of the parent function y = x² lies on the origin. It also has a domain of all real numbers and a range of [0, ∞). Observe that this function increases when x is positive and decreases while x is negative.

A good application of quadratic functions is projectile motion. We can observe an object’s projectile motion by graphing the quadratic function that represents it.

Cubic Functions

Let’s move on to the parent function of polynomials with 3 as its highest degree. Cubic functions share a parent function of y = x³. This function is increasing throughout its domain.

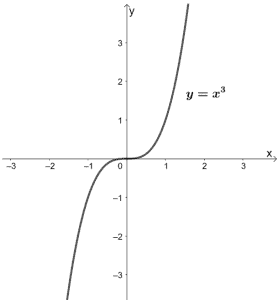
As with the two previous parent functions, the graph of y = x³ also passes through the origin. Its domain and range are both (-∞, ∞) or all real numbers as well.

Absolute Value Functions

The parent function of absolute value functions is y = |x|. As shown from the parent function’s graph, absolute value functions are expected to return V-shaped graphs.

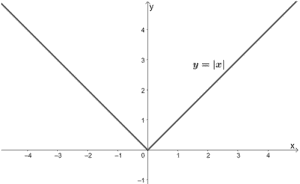
The vertex of y = |x| is found at the origin as well. Since it extends on both ends of the x-axis, y= |x| has a domain at (-∞, ∞).  Absolute values can never be negative, so the parent function has a range of [0, ∞).

We use absolute value functions to highlight that a function’s value must always be positive.

Radical Functions

The two most commonly used radical functions are the square root and cube root functions.

The parent function of a square root function is y = √x. Its graph shows that both its x and y values can never be negative.

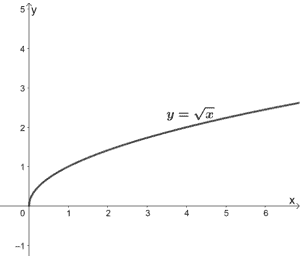
This means that the domain and range of y = √x are both [0, ∞). The starting point or vertex of the parent function is also found at the origin. The parent function y = √x is also increasing throughout its domain.

Let’s now study the parent function of cube root functions. Similar to the square root function, its parent function is expressed as y = ∛x.

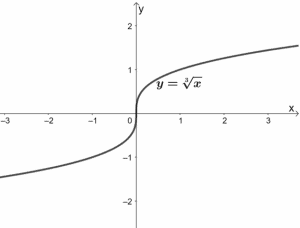
The graph shows that the parent function has a domain and range of (-∞, ∞). We can also see that y = ∛x is increasing throughout its domain.

Exponential Functions

Exponential functions are functions that have algebraic expressions in their exponent. Their parent function can be expressed as y = b^x, where b can be any nonzero constant. The parent function graph, y = e^x, is shown below, and from it, we can see that it will never be equal to 0.

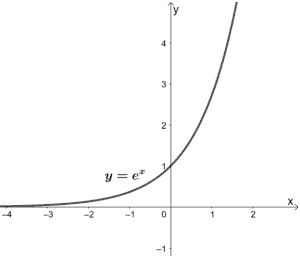
And when x = 0, y passing through the y-axis at y = 1. We can also see that the parent function is never found below the y-axis, so its range is (0, ∞). Its domain, however, can be all real numbers. We can also see that this function is increasing throughout its domain.

One of the most common applications of exponential functions is modeling population growth and compound interest.

Logarithmic Functions

Logarithmic functions are the inverse functions of exponential functions. Its parent function can be expressed as y = log_b x, where b is a nonzero positive constant. Let’s observe the graph when b = 2.

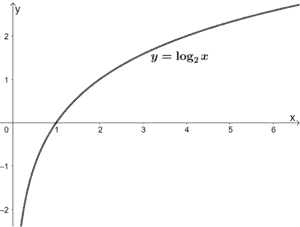
Like the exponential function, we can see that x can never be less than or equal to zero for y = log₂x. Hence, its domain is (0,∞).  Its range, however, contains all real numbers. We can also see that this function is increasing throughout its domain.

We use logarithmic functions to model natural phenomena such as an earthquake’s magnitude. We also apply it when calculating the half-life decay rate in physics and chemistry.

Reciprocal Functions

Reciprocal functions are functions that contain a constant numerator and x as its denominator. Its parent function is y = 1/x.

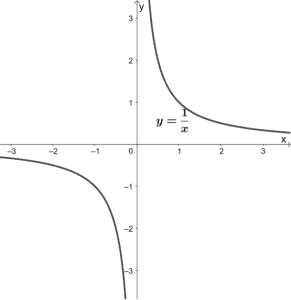
As can be seen from its graph, both x and y can never be equal to zero. This means that its domain and range are (-∞, 0) U (0, ∞). We can also see that the function is decreasing throughout its domain.

There are many other parent functions throughout our journey with functions and graphs, but these eight parent functions are that of the most commonly used and discussed functions.

You can even summarize what you’ve learned so far by creating a table showing all the parent functions’ properties.

How to find the parent function?

What if we’re given a function or its graph, and we need to identify its parent function? We can do this by remembering each function’s important properties and identifying which of the parent graphs we’ve discussed match the one that’s given.

Here are some guide questions that can help us:

• What is the function’s highest degree?
• Does it contain a square root or cube root?
• Is the function found at the exponent or denominator?
• Is the function’s graph decreasing or increasing?
• What is the function’s domain or range?

If we can answer some of these questions by inspection, we will be able to deduce our options and eventually identify the parent function.

Let’s try f(x) = 5(x – 1)². We can see that the highest degree of f(x) is 2, so we know that this function is a quadratic function. Hence, its parent function is y = x².

Why don’t we graph f(x) and confirm our answer as well?

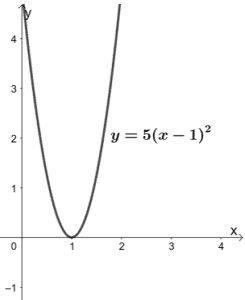
From the graph, we can see that it forms a parabola, confirming that its parent function is y = x².

Review the first few sections of this article and your own notes, then let’s try out some questions to check our knowledge on parent functions.

Example 1

Graphs of the five functions are shown below. Which of the following functions do not belong to the given family of functions?

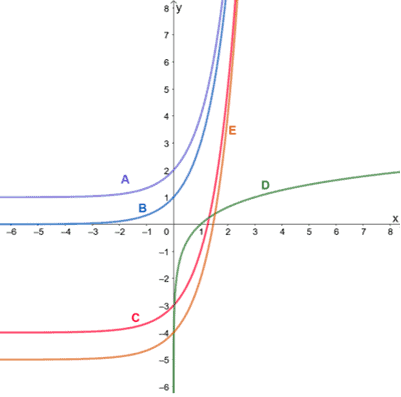
Solution

The functions represented by graphs A, B, C, and E share a similar shape but are either translated upward or downward. In fact, these functions represent a family of exponential functions. This means that they also all share a common parent function:  y=b^x.

On the other hand, the graph of D represents a logarithmic function, so D does not belong to the group of exponential functions.

Example 2

Which of the following functions do not belong to the given family of functions?

• y = 5x²
• y = -2x² + 3x – 1
• y = x(3x²)
• y = (x – 1)(x + 1)

Solution

The function y = 5x² has the highest degree of two, so it is a quadratic function. This means that its parent function is y = x². The same goes for y = -2x² + 3x – 1. From this, we can confirm that we’re looking at a family of quadratic functions.

Applying the difference of perfect squares on the fourth option, we have y = x² – 1. This is also a quadratic function. That leaves us with the third option.

When expanded, y = x(3x²) becomes y = 3x^3, and this shows that it has 3 as its highest degree. Hence, it can’t be part of the given family of functions.

Example 3

 Identify the parent function of the following functions based on their graphs. Define each function’s domain and range as well.

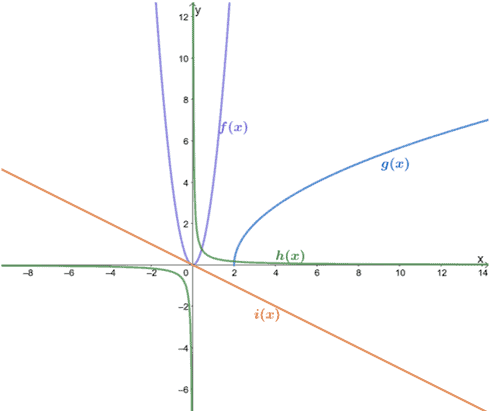
Solution

Let’s start with f(x). We can see that it has a parabola for its graph, so we can say that f(x) is a quadratic function.

• This means that f(x) has a parent function of y = x².
• The graph extends on both sides of x, so it has a domain of (-∞, ∞).
• The parabola never goes below the x-axis, so it has a range of [0,∞).

Based on the graph, we can see that the x and y values of g(x) will never be negative. They also show an increasing curve that resembles the graph of a square root function.

• Hence, the parent function of g(x) is y = √x.
• The graph extends to the right side of x and is never less than 2, so it has a domain of [2, ∞).
• The parabola never goes below the x-axis, so it has a range of [0,∞).

The h(x) graph shows that their x and y values will never be equal to 0. The symmetric curves also look like the graph of reciprocal functions.

• This means that h(x) has a parent function of y = 1/x.
• As long as the x and y are never equal to zero, h(x) is still valid, so it has both a domain and range of (-∞, ∞).

The straight lines representing i(x) tells that it is a linear function.

• It has a parent function of y = x.
• The graph extends on both sides of x and y, so it has a domain and range of (-∞, ∞).

Example 4

Identify the parent function of the following functions.

• f(x) = x³ – 2x + 1
• g(x) = 3√x + 1
• h(x) = 4/ x
• i(x) = e ^{x + 1}

Solution

• The highest degree of f(x) is 3, so it’s a cubic function. This means that it has a parent function of y = x³.
• The function g(x) has a radical expression, 3√x. Since it has a term with a square root, the function is a square root function and has a parent function of y = √x.
• We can see that x is found at the denominator for h(x), so it is reciprocal. Hence, its parent function is y = 1/x.
• The function’s exponents contain x, so this alone tells us that i(x) is an exponential function. Hence, its parent function can be expressed as y = b^x, where b is a constant. For the case of i(x), we have y = e^x as its parent function.