Pascal’s triangle – Definition, Patterns, and Applications

Pascal’s Triangle is a number pattern that is known for its shape – yes, a triangle! This interesting pattern and property is named after Blaise Pascal and has been a famous triangle in mathematics due to its extensive application in algebra, number theory, and statistics.

Pascal’s Triangle is a number pattern that returns the values or coefficients used in binomial expansions. The numbers in the next layer will depend on the sum of two terms positioned above them in the previous layer.

You may already have encountered this unique triangle in your earlier math classes, so in this article, we’ll dive deeper into understanding how we can apply Pascal’s Triangle in algebra and statistics.

• Make sure to review your knowledge of the binomial theorem.
• Keep your notes on permutation and combination handy.

For now, let’s refresh our knowledge and take a look at the important properties of a Pascal’s Triangle.

What is Pascal’s Triangle?                

The Pascal’s Triangle is a number pattern that shows a significant number of patterns used to expand binomial expressions. Before we dive right into its application in statistics, let’s observe the image shown below.

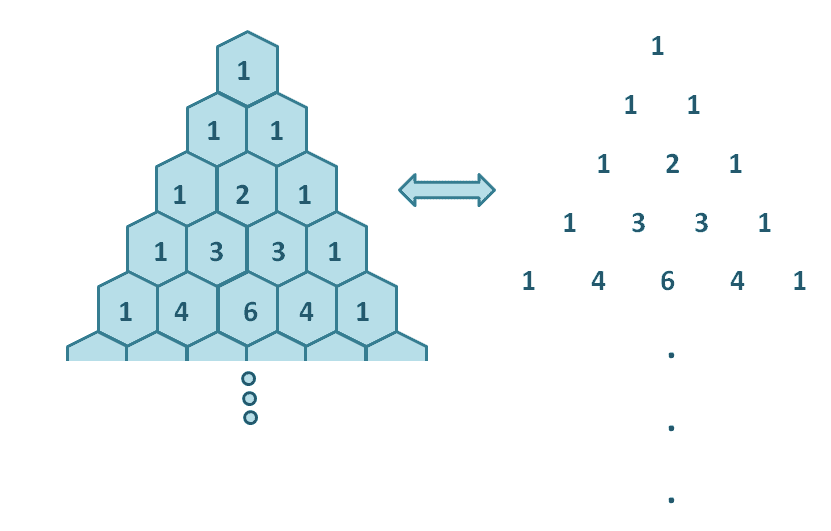
The best way to remember the definition of Pascal’s Triangle and its properties is by constructing the Pascal’s Triangle itself, as shown above.

As can be seen, the values in the middle of the third row can be determined by adding the two consecutive terms in the second row. Similarly, the center of the fourth row’s values are the results of the consecutive terms from the third row are added.

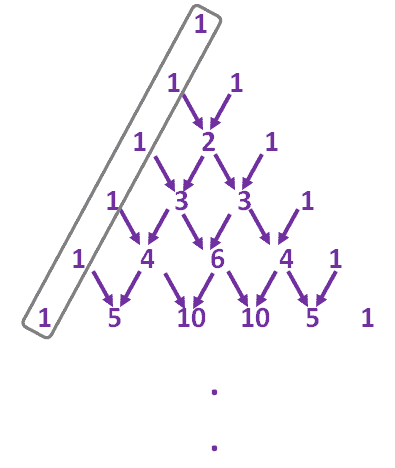
Here’s an extended version of Pascal’s Triangle shown, and it shows how the sixth row can be formed by:
• Using $1$ at the ends of the row.
• Adding two consecutive terms to find the term found below them in the next row.
The arrows guide the two numbers that were added to find the next row’s term.

Pascal’s Triangle definition and hidden patterns

Generalizing this observation, Pascal’s Triangle is simply a group of numbers that are arranged where each row of values represents the coefficients of a binomial expansion, $(a+ b)^n$.

The rows’ values can be determined by adding two consecutive numbers above each value, as shown in the earlier section.

Why don’t we go ahead and arrange Pascal’s Triangle’s values and justify them to the left? This will help us observe the most interesting patterns there are within these numbers.

\begin{aligned}&1\\&1\phantom{xxxx}1\\&1\phantom{xxxx}2\phantom{xxxx}1\\&1\phantom{xxxx}3\phantom{xxxx}3\phantom{xxxx}1\\&1\phantom{xxxx}4\phantom{xxxx}6\phantom{xxxx}4\phantom{xxxx}1\\&.\\&.\\&.\end{aligned}
We can begin by adding all the terms in each row and observe the result. What can you observe?
\begin{aligned}&1\phantom{x} = \phantom{x} 1\\&1\phantom{x}+\phantom{x}1\phantom{x} = \phantom{x}2\\&1\phantom{x}+\phantom{x}2\phantom{x}+\phantom{x}1\phantom{x} = \phantom{x} 4\\&1\phantom{x}+\phantom{x} 3\phantom{x}+\phantom{x}3\phantom{x}+\phantom{x} 1\phantom{x}=\phantom{x} 8\\&1\phantom{x}+\phantom{x} 4\phantom{x}+\phantom{x} 6\phantom{x}+\phantom{x} 4\phantom{x}+\phantom{x}1\phantom{x}=\phantom{x}16\\&.\\&.\\&.\end{aligned}

We can see that each row’s sum is actually equal to the power of $2$ that depends on the number of rows.

From this, we can see that the sum of the given Pascal’s Triangle’s row is in fact equal to $2^{n -1}$, where $n$ is the row number.

Here’s another interesting pattern about Pascal’s Triangle: when we treat them as digits and combine one row’s values into one number, we will end up with a power of $11$.
\begin{aligned}1&= 11^0\\11&=11^1\\121&=11^2\\1331&=11^3\\14641 &= 11^4\end{aligned}
Does this still apply for rows with two-digit values? Yes, what can be done is to carry over the tens place to the previous value.
Amazing isn’t it? Here’s a third one for now:
\begin{aligned}&1 \\&1 \phantom{xxxx}\color{blue} 1\\&{\color{blue}1 }\phantom{xxxx}{\color{red} 2}\phantom{xxxx}{\color{green} 1}\\&{\color{red} 1}\phantom{xxxx}{\color{green} 3}\phantom{xxxx}{\color{blue} 3}\phantom{xxxx} 1\\&{\color{green}1}\phantom{xxxx}{\color{blue} 3}\phantom{xxxx} 6\phantom{xxxx} 4\phantom{xxxx}1\\&{\color{blue}1}\phantom{xxxx} 5\phantom{xxxx} 10\phantom{xxxx} 10\phantom{xxxx} 5\phantom{xxxx}1\\&.\\&.\\&.\end{aligned}
The first few sums of the terms along the diagonal of Pascal’s Triangle are $1, 1, 2, 3, 5, 8,…$. These are the first six terms of the Fibonacci sequence. Amazing how different math concepts can be observed in this simple number pattern?
One important pattern from Pascal’s Triangle has been extensively studied and also has important applications in binomial expansion and combinatorial numbers.

How to use Pascal’s Triangle?  

Here’s an interesting way to view the Pascal’s Triangle in terms of combinatorial numbers. Before we proceed, recall that $\binom{n}{r} = \dfrac{n!}{r! N!}$. If you need a quick refresher on what these symbols represent, check out this article as well.
\begin{aligned} \binom{0}{0}\phantom{xxxxxxxxxxxx}\\\binom{1}{0} \phantom{xxxx}\binom{1}{1}\phantom{xxxxxxxx}\\\phantom{xx}\binom{2}{0} \phantom{xxx}\binom{2}{1}\phantom{xxx}\binom{2}{2}\phantom{xzxxx}\\\binom{3}{0} \phantom{xxx}\binom{3}{1}\phantom{xxx}\binom{3}{2}\phantom{xx}\binom{3}{3}\phantom{xxx}\end{aligned}
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxx} 1\phantom{xxxxxxxxxx}\\\text{Second Row:}\phantom{xxxxxxxxxxx} 1\phantom{xxxx} 1\phantom{xxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxx}\\\text{Fourth Row:}\phantom{xxxxxxx} 1\phantom{xxxx} 3\phantom{xxx}{\color{blue} 3}\phantom{xxx} 1\phantom{xxx}\\\text{Fifth Row:}\phantom{xxx}1\phantom{xxxx} 4\phantom{xxxx} 6\phantom{xxxx} 4\phantom{xxxx}1\\.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\end{aligned}
This means that if we want to find the value of $\binom{\color{blue}3}{\color{red}2}$, we simply inspect the value that is located at the $\color{blue} 3 + 1 = 4$th row and $\color{red} 2 + 1 =3$rd value to the right. This means that $\binom{3}{2} = 2$.

How to apply Pascal’s Triangle formula?

Let’s use what we’ve learned about Pascal’s Triangle and apply these in expanding binomial theorems and combinatorics. Recall that $\binom{n}{r}$ simply means that we choose $n$ from $r$.

Applying the Pascal’s Triangle to Find $\boldsymbol{\binom{n}{r}}$

From what we’ve observed, we can find the value of $\binom{n}{r}$ using the values found in the Pascal’s Triangle:
• Complete the Pascal’s Triangle up to $(n + 1)$ rows.
• Focus on the $(n +1)$th row of the triangle.
• Find the value located at the $(r + 1)$th position of the row we’re focusing on.
Once we locate that particular value, we now have $\binom{n}{r}$. Yes, it’s that easy!
This means that $\binom{4}{2}$ is equivalent to the value of the Pascal’s Triangle located at the $5$th row and the $3$rd term from the right.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxx} 1\phantom{xxxxxxxxxx}\\\text{Second Row:}\phantom{xxxxxxxxxxx} 1\phantom{xxxx} 1\phantom{xxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx}1\phantom{xxxx}\\\text{Fourth Row:}\phantom{xxxxxxx}1 \phantom{xxxx} 3\phantom{xxx} 3\phantom{xxx}1\phantom{xxx}\\\text{Fifth Row:}\phantom{xxx}1\phantom{xxxx}4\phantom{xxxx}{\color{blue}6}\phantom{xxxx}4\phantom{xxxx}1\\.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\end{aligned}
This means that $\binom{4}{2}$ is equal to $6$.

Applying the Pascal’s Triangle in Binomial Expansion

We can extend this formula when expanding binomials to the $n$th power. Let’s do a quick recap of the binomial expansion’s formula:

\begin{aligned}(a+ b)^n &= \sum_{k=0}^{n} \binom{n}{k}a^{n-k}b^k\\&=a^n + \binom{n}{1}a^{n-1}b+\binom{n}{2}a^{n-2}b^2 + … +\binom{n}{n -1}a^{1}b^{n- 1} + b^n \end{aligned}
Remember that we can find the values of $\binom{n}{k}$ using the Pascal’s Triangle. In fact, the entire coefficients of the expansion can be determined by using the coefficients of the $(n + 1)$ row of the Pascal’s Triangle.
For example, if we want to find the coefficients of $(a + b)^3$ once it’s expanded, we inspect the values found on the $3 + 1=4$th or fourth row of the given Pascal’s triangle.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxx}1 \phantom{xxxxxxxxxx}\\\text{Second Row:}\phantom{xxxxxxxxxx} 1\phantom{xxxx} 1\phantom{xxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxx} 1\phantom{xxxx}2 \phantom{xxxx} 1\phantom{xxxx}\\\color{green}\text{Fourth Row:}\phantom{xxxxxxx}1\phantom{xxxx}3\phantom{xxx} 3\phantom{xxx} 1\phantom{xx}\\\text{Fifth Row:}\phantom{xxx}1\phantom{xxxx} 4\phantom{xxxx} 6\phantom{xxxx} 4\phantom{xxx}1\\.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\\\phantom{xxxxxxxxxx}.\phantom{xxxxxxxxxx}\end{aligned}
From this, we can see that the coefficients of the expansion are $1, 3, 3, 1$ in a particular order. These are the coefficients of the expansion, so we can now complete the expansion.
\begin{aligned}(a + b)^3 &= \underline{\phantom{xxx}}a^3 + \underline{\phantom{xxx}}a^2b + \underline{\phantom{xxx}}ab^2+\underline{\phantom{xxx}}b^3\end{aligned}

This means that we have expanded $(a + b)^3$ using Pascal’s Triangle’s values, as shown below.

\begin{aligned}(a + b)^3 &= {\color{green}1}a^3 + {\color{green}3}a^2b + {\color{green}3}ab^2+{\color{green}1}b^3\\&=a^3 + 3a^2b + 3ab^2 + b^3\end{aligned}

Here’s a quick recap of when we want to expand $(a + b)^n$ and use Pascal’s Triangle values.

Step 1: Write down the first $(n +1)th row of the Pascal’s Triangle.

Step 2:The terms of the combination will have $(a + b)^n = \underline{\phantom{xxx}}a^n + \underline{\phantom{xxx}}a^{n-1}b^1 + … + \underline{\phantom{xxx}}ab^{n -1}+\underline{\phantom{xxx}}b^n$.

Step 3:Use the values of the $(n +1)$th row to fill in the coefficients of the partial expansion from the previous step.

That’s it! Don’t worry; we’ll review what we’ve learned so far and apply them to answer the examples shown below.

Example 1

Write down the first seven rows of the known Pascal’s Triangle to answer the following expression.

a. What is the sum of the values found in the seventh row?

b. What is the value of $11^6$?

Solution

Let’s write down the first seven rows of the Pascal’s Triangle first and highlight the seventh row:

\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxxxxxxxxxxx}1\phantom{xxxxxxxxxxxxxx}\\\text{Second Row:} \phantom{xxxxxxxxxxxxxxxxxxx}1\phantom{xxxxx} 1\phantom{xxxxxxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxxxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxxxxxxx}\\\text{Fourth Row:}\phantom{xxxxxxxxxxxxxx} 1\phantom{xxxx} 3\phantom{xxxx}3\phantom{xxxx}1\phantom{xxxxxxx}\\\text{Fifth Row:}\phantom{xxxxxxxxsxx} 1\phantom{xxxx} 4\phantom{xxxx} 6 \phantom{xxxx} 4\phantom{xxxx}1 \phantom{xxxxx}\\\text{Sixth Row:}\phantom{xxxxxxx}1\phantom{xxxx} 5\phantom{xxxx}10\phantom{xxxx} 10\phantom{xxxx}5\phantom{xxxx}1\phantom{xx}\\\color{green}\text{Seventh Row:}\phantom{xxx} 1\phantom{xxxx} 6\phantom{xxxx}15\phantom{xxxx} 20\phantom{xxxx} 15\phantom{xxxx} 6 \phantom{xxxx}1\end{aligned}

As we have discussed in the earlier section, the sum of the values found at the $n$th row is equivalent to $2^{n – 1}$. Since we want to find the sum of the seventh row’s values, we find the value of $2^{7 – 1}$ equal to $2^6 = 64$.
We can also confirm this by actually adding the terms from the seventh row:
\begin{aligned}&{\color{green} \text{Seventh Row}}: 1 \phantom{xx} 6\phantom{xx}15\phantom{xx} 20\phantom{xx}15\phantom{xx} 6 \phantom{xx}1\\&\phantom{xxxxxxxxx}=1 \phantom{x} +\phantom{x} 6\phantom{x} +\phantom{x} 15\phantom{xx} 20\phantom{x} +\phantom{x}15\phantom{x} +\phantom{x} 6\phantom{x} +\phantom{x}1\\&\phantom{xxxxxxxxx}=64\end{aligned}
a. Hence, the sum values of found at the seventh row is equal to $64$.
To find the value of $11^6$, we inspect the values found at the $(6 + 1)= 7$th row of the Pascal’s Triangle.
We can see that the values of the seventh row are: $1 \phantom{x} 6\phantom{x}15\phantom{x} 20\phantom{x}15\phantom{x} 6 \phantom{x}1$. We can use these to find the value of $11^6$: use these values and carry the tens place over for instances where the values have two digits.
\begin{aligned}&\phantom{xx}1 \phantom{x} 6\phantom{x}15\phantom{x} 20\phantom{x}15\phantom{x} 6 \phantom{x}1\\&=1 \phantom{x} 6^{\color{green} + 1}\phantom{x}5^{\color{green} + 2}\phantom{x} 0^{\color{green} + 1}\phantom{x}5\phantom{x} 6 \phantom{x}1\\&=1 \phantom{x}7 \phantom{x}7 \phantom{x}1 \phantom{x}5 \phantom{x}6 \phantom{x}1\phantom{xxx}\end{aligned}
b. This means that $11^6$ is equal to $1, 771, 561$.

Example 2

Determine the values of the following using a Pascal’s Triangle.

a. $\binom{5}{4}$
b. $\binom{4}{1}$
c. $\binom{6}{2}$

Solution

When we have a Pascal’s Triangle, we can actually find the value of $\binom{n}{r}$ by finding the value located at the $(n + 1)$th term and $(r + 1)$th unit/s to the right. Let’s use the same Pascal Triangle for all three, so it helps to write down the first seven rows for this item.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxxxxxxxxxxx}1\phantom{xxxxxxxxxxxxxx}\\\text{Second Row:} \phantom{xxxxxxxxxxxxxxxxxxx}1\phantom{xxxxx} 1\phantom{xxxxxxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxxxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxxxxxxx}\\\text{Fourth Row:}\phantom{xxxxxxxxxxxxxx} 1\phantom{xxxx} 3\phantom{xxxx}3\phantom{xxxx}1\phantom{xxxxxxx}\\\text{Fifth Row:}\phantom{xxxxxxxxsxx} 1\phantom{xxxx} 4\phantom{xxxx} 6 \phantom{xxxx} 4\phantom{xxxx}1 \phantom{xxxxx}\\\text{Sixth Row:}\phantom{xxxxxxx}1\phantom{xxxx} 5\phantom{xxxx}10\phantom{xxxx} 10\phantom{xxxx}5\phantom{xxxx}1\phantom{xx}\\\text{Seventh Row:}\phantom{xxx} 1\phantom{xxxx} 6\phantom{xxxx}15\phantom{xxxx} 20\phantom{xxxx} 15\phantom{xxxx} 6 \phantom{xxxx}1\end{aligned}
For the first item, we simply find the value located at the $6+1 = 6$th or sixth row and $4 + 1 = 5$ units to the right.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxxxxxxxxxxx}1\phantom{xxxxxxxxxxxxxx}\\\text{Second Row:} \phantom{xxxxxxxxxxxxxxxxxxx}1\phantom{xxxxx} 1\phantom{xxxxxxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxxxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxxxxxxx}\\\text{Fourth Row:}\phantom{xxxxxxxxxxxxxx} 1\phantom{xxxx} 3\phantom{xxxx}3\phantom{xxxx}1\phantom{xxxxxxx}\\\text{Fifth Row:}\phantom{xxxxxxxxsxx} 1\phantom{xxxx} 4\phantom{xxxx} 6 \phantom{xxxx} 4\phantom{xxxx}1 \phantom{xxxxx}\\\text{Sixth Row:}\phantom{xxxxxxx}1\phantom{xxxx} 5\phantom{xxxx}10\phantom{xxxx} 10\phantom{xxxx}{\color{red}5}\phantom{xxxx}1\phantom{xx}\\\text{Seventh Row:}\phantom{xxx} 1\phantom{xxxx} 6\phantom{xxxx}15\phantom{xxxx} 20\phantom{xxxx} 15\phantom{xxxx} 6 \phantom{xxxx}1\end{aligned}
We’ll apply a similar process for b and c – note that for Pascal’s Triangle shown below, the value of $\binom{4}{1}$ is marked in green, and $\binom{6}{2}$ is marked in blue.
• For $\color{green}\binom{4}{1}$, find the second value in the fifth row.
• Similarly, to find $\color{blue}\binom{6}{2}$, find the third value of the seventh row.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxxxxxxxxxxx}1\phantom{xxxxxxxxxxxxxx}\\\text{Second Row:} \phantom{xxxxxxxxxxxxxxxxxxx}1\phantom{xxxxx} 1\phantom{xxxxxxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxxxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxxxxxxx}\\\text{Fourth Row:}\phantom{xxxxxxxxxxxxxx} 1\phantom{xxxx} 3\phantom{xxxx}3\phantom{xxxx}1\phantom{xxxxxxx}\\\text{Fifth Row:}\phantom{xxxxxxxxsxx} 1\phantom{xxxx} {\color{green} 4}\phantom{xxxx} 6 \phantom{xxxx} 4\phantom{xxxx}1 \phantom{xxxxx}\\\text{Sixth Row:}\phantom{xxxxxxx}1\phantom{xxxx} 5\phantom{xxxx}10\phantom{xxxx} 10\phantom{xxxx}5 \phantom{xxxx}1\phantom{xx}\\\text{Seventh Row:}\phantom{xxx} 1\phantom{xxxx} 6\phantom{xxxx}{\color{blue} 15}\phantom{xxxx} 20\phantom{xxxx} 15\phantom{xxxx} 6 \phantom{xxxx}1\end{aligned}
Hence, we have the following values:
a. $\binom{5}{4} = 6$
b. $\binom{4}{1} = 4$
c. $\binom{6}{2} = 15$

Example 3

Expand the following expressions using the known Pascal’s Triangle.

a. $(a – b)^3$
b. $(4x + 3y)^4$

Solution

Since we’re working with expanding binomials to powers of $3$ and $4$, we can begin by writing the first five rows of the Pascal’s Triangle. Highlight the $(3 + 1) =4$th and $(4 + 1) = 5$th rows.
\begin{aligned}\text{First Row:}\phantom{xxxxxxxxxxxxxxxxxxxxxx}1\phantom{xxxxxxxxxxxxxx}\\\text{Second Row:} \phantom{xxxxxxxxxxxxxxxxxxx}1\phantom{xxxxx} 1\phantom{xxxxxxxxxxx}\\\text{Third Row:}\phantom{xxxxxxxxxxxxxxxxx} 1\phantom{xxxx} 2\phantom{xxxx} 1\phantom{xxxxxxxxx}\\\color{blue}\text{Fourth Row:}\phantom{xxxxxxxxxxxxxx} 1\phantom{xxxx} 3\phantom{xxxx}3\phantom{xxxx}1\phantom{xxxxxxx}\\\color{green}\text{Fifth Row:}\phantom{xxxxxxxxsxx} 1\phantom{xxxx} 4\phantom{xxxx} 6 \phantom{xxxx} 4\phantom{xxxx}1 \phantom{xxxxx}\end{aligned}
We’ll use the fourth row’s values for the coefficients. The only tricky part about the first binomial is the minus sign in between. Just make sure to include this when expanding the powers of $-b$.
\begin{aligned}(a + b)^3 &= {\color{green}1}a^3 + {\color{green}3}a^2b + {\color{green}3}ab^2+{\color{green}1}b^3\\&=a^3 + 3a^2b + 3ab^2 + b^3\end{aligned}
a. Hence, we have $(a – b)^3= a^3 – 3a^2b + 3ab^2 – b^3$.
We’ll apply a similar approach to expand $(4x + 3y)^4$, but this time, we use the fifth row of the Pascal’s Triangle and use $4x$ and $3y$ in the variable parts as shown below.
\begin{aligned}(4x + 3y)^4&= \underline{\phantom{xxx}}(4x)^4 + \underline{\phantom{xxx}}(4x)^3(3y) + \underline{\phantom{xxx}}(4x)^2(3y)^2 +\underline{\phantom{xxx}}(4x)^1(3y)^3+(3y)^4 \\ &= {\color{green}1}(256x^4) + {\color{green}4}(64x^3)(3y) + {\color{green}6}(16x^2)(9y^2)+ {\color{green}4}(4x)(27y^3)+{\color{green}1}81y^4\\&=256x^4 +768x^3y + 864x^2y^2 + 432xy^3+ 81y^4\end{aligned}
b. This means that $(4x + 3y)^4 = 256x^4 +768x^3y + 864x^2y^2 + 432xy^3+ 81y^4$.